 |
Момент импульса системы материальных точек
|
|
|
|
Если в задаче рассматривается не одна материальная точка, а система точек, то момент импульса системы равен векторной сумме моментов импульсов всех материальных точек системы
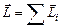 ,
,
где все векторы 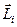 определены относительно одной и той же точки заданной системы отсчета.
определены относительно одной и той же точки заданной системы отсчета.
Сумма моментов всех внутренних сил будет равна нулю, так как силы, с которыми взаимодействуют любые две материальные точки системы, удовлетворяют третьему закону Ньютона и действуют вдоль одной прямой, поэтому их плечи одинаковые, а направления противоположные.
Закон изменения момента импульса для системы тел имеет вид
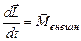 ,
,
то есть изменение момента импульса системы равно сумме моментов всех внешних сил относительно той же точки.
Если сумма моментов всех внешних сил равна нулю, то момент импульса системы сохраняется
 .
.
Как и в случае закона сохранения импульса, момент импульса незамкнутой системы сохраняется при условии что:
1) суммарный момент внешних сил равен нулю,
2) если момент внешних сил относительно точки отличен от нуля, но относительно некоторой оси равен нулю, то момент импульса относительно этой оси сохраняется,
3) если действие внешних сил ограничено во времени 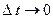 (удар, взрыв), то изменением момента импульса
(удар, взрыв), то изменением момента импульса 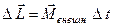 за время удара можно пренебречь.
за время удара можно пренебречь.
Ранее было показано, что в некоторых случаях решение задач, связанных с импульсом системы, упрощается, если их решать в системе центра масс (раздел IV). Решение задач на момент импульса также упрощается в этой системе отсчета. Это связано с тем, что полный импульс системы частиц в системе центра масс равен нулю, и поэтому момент импульса системы не зависит от выбора точки, относительно которой его определяют. Поэтому этот момент называют собственным моментом импульса и обозначают 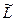 . Момент импульса
. Момент импульса  системы частиц в произвольной системе складывается из ее собственного момента импульса
системы частиц в произвольной системе складывается из ее собственного момента импульса 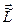 и момента
и момента 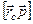 , обусловленного движением системы частиц как целого
, обусловленного движением системы частиц как целого
|
|
|
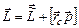 .
.
Решение задач
 6.4. Шарик массы m, двигавшийся со скоростью
6.4. Шарик массы m, двигавшийся со скоростью 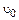 испытал упругое лобовое столкновение с одним из шариков покоившейся жесткой гантели (рис.52). Масса каждого шарика гантели равна m/2, длина легкого соединительного стержня гантели - l. Считая шарики материальными точками, найдите:
испытал упругое лобовое столкновение с одним из шариков покоившейся жесткой гантели (рис.52). Масса каждого шарика гантели равна m/2, длина легкого соединительного стержня гантели - l. Считая шарики материальными точками, найдите:
а) скорость каждого шарика сразу после соударения,
б)* скорость центра масс системы после соударения,
в)* собственный момент импульса 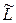 гантели (в системе центра масс).
гантели (в системе центра масс).
Решение. а) Рассмотрим момент импульса системы относительно точки соударения (шарик 2 рис.52). Относительно этой точки момент импульса системы до столкновения равен нулю. Рассматриваемая система является замкнутой, поэтому момент импульса сохраняется и остается равным нулю. Следовательно, после столкновения скорость нижнего шарика гантели равна нулю  (т.к. плечо импульса 3 шарика не равно нулю, а плечи импульсов 1 и 2 шариков равны нулю).
(т.к. плечо импульса 3 шарика не равно нулю, а плечи импульсов 1 и 2 шариков равны нулю).
Поскольку удар абсолютно упругий, импульс и кинетическая энергия системы также сохраняются:
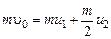 , (1)
, (1)
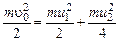 , (2)
, (2)
где 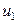 и
и 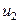 - скорости отлетевшего шарика (шарик 1 рис.52) и верхнего шарика гантели (шарик 2 рис.52) сразу после удара. Решая совместно уравнения (1) и (2), найдем скорость верхнего шарика гантели и скорость отлетевшего шарика сразу после удара
- скорости отлетевшего шарика (шарик 1 рис.52) и верхнего шарика гантели (шарик 2 рис.52) сразу после удара. Решая совместно уравнения (1) и (2), найдем скорость верхнего шарика гантели и скорость отлетевшего шарика сразу после удара
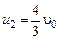 и
и  .
.
б) Момент импульса системы частиц складывается из ее собственного момента импульса  и момента, обусловленного движением системы частиц как целого
и момента, обусловленного движением системы частиц как целого  :
:
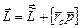 , (3)
, (3)
где  и
и 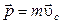 - радиус-вектор центра масс и суммарный импульс системы частиц соответственно. Так как момент импульса системы после столкновения равен нулю, из уравнения (3) следует, что собственный момент импульса гантели после столкновения равен:
- радиус-вектор центра масс и суммарный импульс системы частиц соответственно. Так как момент импульса системы после столкновения равен нулю, из уравнения (3) следует, что собственный момент импульса гантели после столкновения равен:
|
|
|
 .
.
Центр масс гантели после столкновения (также как и до столкновения) находится посередине соединительного стержня, т.е. 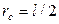 , скорость ее центра масс
, скорость ее центра масс
 .
.
в) Учитывая, что 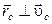 получим искомую величину:
получим искомую величину:
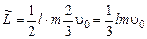 .
.
6.5. Гладкий горизонтальный диск вращают относительно Земли, вращение которой не учитывается, с угловой скоростью 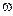 вокруг вертикальной оси, проходящей через его центр - точку 0. Из этой точки в момент
вокруг вертикальной оси, проходящей через его центр - точку 0. Из этой точки в момент  пустили небольшую шайбу массой m со скоростью
пустили небольшую шайбу массой m со скоростью 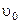 . Найдите момент импульса шайбы
. Найдите момент импульса шайбы  относительно точки 0 в системе отсчета связанной с диском.
относительно точки 0 в системе отсчета связанной с диском.
Решение. Система отсчета, связанная с вращающимся диском, является неинерциальной системой отсчета. В этой системе момент импульса шайбы относительно точки 0 равен
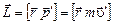 ,
,
где 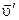 - скорость шайбы относительно диска. Раскрыв векторное произведение, получим
- скорость шайбы относительно диска. Раскрыв векторное произведение, получим
 ,
,
где  - угол между векторами
- угол между векторами  и
и 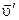 . Из условия задачи известна скорость шайбы относительно Земли, которая является инерциальной системой отсчета -
. Из условия задачи известна скорость шайбы относительно Земли, которая является инерциальной системой отсчета - 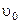 . Запишем связь между скоростями шайбы в этих системах отсчета
. Запишем связь между скоростями шайбы в этих системах отсчета
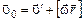 .
.
 Выразим из последнего выражения
Выразим из последнего выражения 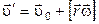 и определим ее направление (рис.53). Из рисунка видно, что вектор
и определим ее направление (рис.53). Из рисунка видно, что вектор 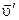 является диагональю прямоугольника, значит
является диагональю прямоугольника, значит  . Учитывая, что
. Учитывая, что 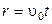 , найдем момент импульса шайбы
, найдем момент импульса шайбы  относительно точки 0 в системе отсчета связанной с диском, подставив найденные величины в исходное выражение
относительно точки 0 в системе отсчета связанной с диском, подставив найденные величины в исходное выражение
 .
.
А направление вектора 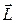 покажем на рис.53.
покажем на рис.53.
|
|
|


