 |
Уравнения движения твердого тела
|
|
|
|
В динамике твердого тела рассматривают два основных вида движения – поступательное и вращательное. При поступательном движении отрезок, соединяющий любые две точки тела, перемещается параллельно самому себе. Поскольку все точки тела движутся одинаково, достаточно описать движение одной точки. При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения (при этом скорости всех точек перпендикулярны оси вращения).
Плоское движение твердого тела можно представить как совокупность двух основных видов движения - вращательного относительно какой-либо оси и поступательного со скоростью оси.
Обычно ось вращения выбирают так, чтобы она проходила через центр масс тела. Поступательное движение центра масс описывается вторым законом Ньютона, а вращательное движение в системе центра масс описывается уравнением моментов
 ;
;  ,
,
где  - момент инерции твердого тела относительно оси вращения. При качении однородного цилиндра (шара, колеса) по плоскости без проскальзывания между линейными величинами, характеризующими движение центра масс тела (скоростью
- момент инерции твердого тела относительно оси вращения. При качении однородного цилиндра (шара, колеса) по плоскости без проскальзывания между линейными величинами, характеризующими движение центра масс тела (скоростью  и ускорением
и ускорением  ), и угловыми величинами (угловой скоростью
), и угловыми величинами (угловой скоростью  и угловым ускорением
и угловым ускорением  ), определяющими вращательное движение тела, существуют соотношения
), определяющими вращательное движение тела, существуют соотношения
 ,
,
 .
.
Кинетическая энергия плоского движения равна
 .
.
Плоское движение можно рассматривать как чисто вращательное относительно мгновенной оси вращения (раздел II, задача 2.4). Мгновенная ось - это ось, проходящая через неподвижные в данный момент точки тела. Положение мгновенной оси меняется со временем. Например, в случае катящегося по плоскости цилиндра (шара, колеса) мгновенная ось в каждый момент времени совпадает с линией касания цилиндра и плоскости.
|
|
|
При решении задач необходимо:
1) записать второй закона Ньютона для центра масс твердого тела;
2) записать основное уравнения динамики вращательного движения, относительно оси вращения в скалярной форме, заменяя соответствующие величины (угловое ускорение, момент силы и т.д.) проекциями этих векторов на ось вращения;
3) если число записанных уравнений меньше числа неизвестных, то необходимо использовать кинематические и динамические связи между неизвестными. Таким образом, получают систему уравнений, число которых равно числу неизвестных.
 Решение задач
Решение задач
7.4. Тонкий однородный стержень АВ массы  движется поступательно с ускорением
движется поступательно с ускорением  под действием сил
под действием сил  и
и  (рис.58). Найти длину стержня, если расстояние между точками приложения сил равно
(рис.58). Найти длину стержня, если расстояние между точками приложения сил равно  .
.
Решение. По условию задачи стержень движется поступательно, поэтому момент внешних сил, действующих на стержень относительно любой оси равен нулю. Выберем в качестве оси ось, проходящую через центр масс (точка С на рис.58), и направленную перпендикулярно плоскости рисунка, тогда
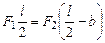 .
.
Центр масс любой системы частиц движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы. Запишем уравнение движения центра масс стержня в проекциях на ось X:
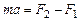 .
.
Решая совместно записанные уравнения, получим искомую величину:
 .
.
7.5. На однородный сплошной цилиндр массы M и радиуса R плотно намотана лёгкая нить, к концу которой прикреплён груз m. В момент t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:
 а) модуля угловой скорости цилиндра;
а) модуля угловой скорости цилиндра;
б) кинетической энергии всей системы.
Решение. а) Система состоит из двух тел (рис.59): груза массы m, движущегося поступательно вдоль оси X, и цилиндра массы M, вращающегося относительно оси Z, проходящей через ось цилиндра, перпендикулярно плоскости рисунка «от нас» (значок  на рис.59).
на рис.59).
|
|
|
На груз действует сила тяжести  и сила натяжения нити
и сила натяжения нити 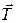 . Составим уравнение движения груза в проекциях на ось X
. Составим уравнение движения груза в проекциях на ось X
 . (1)
. (1)
На цилиндр действуют сила тяжести  , сила реакции крепления
, сила реакции крепления  и сила натяжения нити
и сила натяжения нити  . Вращающий момент относительно оси Z создаёт только сила натяжения нити
. Вращающий момент относительно оси Z создаёт только сила натяжения нити  (поскольку только у этой силы есть плечо относительно оси Z). Составим уравнение движения цилиндра относительно оси Z:
(поскольку только у этой силы есть плечо относительно оси Z). Составим уравнение движения цилиндра относительно оси Z:
 . (2)
. (2)
Момент инерции цилиндра
 . (3)
. (3)
Невесомость нити позволяет считать силу натяжения вдоль всей нити постоянной по модулю
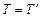 . (4)
. (4)
Если нить не проскальзывает относительно цилиндра, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой ее точке, а, следовательно, и ускорению груза
 . (5)
. (5)
Угловая скорость цилиндра (см. раздел I) равна
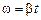 . (6)
. (6)
Решая систему из уравнений (1)-(6) получим выражения для угловой скорости цилиндра
 .
.
б) Кинетическая энергия системы складывается из энергии поступательно движущегося груза и энергии вращающегося цилиндра
 .
.
Учитывая, что 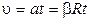 , найдём кинетическую энергию системы
, найдём кинетическую энергию системы
 .
.
7.6. Однородный цилиндр скатывается без скольжения по наклонной плоскости, составляющей угол  с горизонтом. Найти ускорение цилиндра.
с горизонтом. Найти ускорение цилиндра.
 Решение: Направим ось X вдоль наклонной плоскости вниз, а ось Z - перпендикулярно плоскости чертежа, проходящей через центр масс цилиндра (значок
Решение: Направим ось X вдоль наклонной плоскости вниз, а ось Z - перпендикулярно плоскости чертежа, проходящей через центр масс цилиндра (значок  на рис.60). Цилиндр совершает плоское движение – поступательное (вдоль оси X) и вращательное (относительно оси Z).
на рис.60). Цилиндр совершает плоское движение – поступательное (вдоль оси X) и вращательное (относительно оси Z).
Покажем силы, действующие на цилиндр при его движении вниз. На цилиндр действуют сила тяжести  , а со стороны поверхности в нормальном направлении - сила нормальной реакции опоры
, а со стороны поверхности в нормальном направлении - сила нормальной реакции опоры  и против направления движения - сила трения
и против направления движения - сила трения  (рис.60). Поскольку проскальзывания нет, сила трения является силой трения покоя.
(рис.60). Поскольку проскальзывания нет, сила трения является силой трения покоя.
Уравнение поступательного движения цилиндра в проекциях на оси X имеет вид
 ,
,
Уравнение вращательного движения цилиндра относительно оси Z, проходящей через центр цилиндра:
 ,
,
где  - момент инерции цилиндра относительно оси вращения,
- момент инерции цилиндра относительно оси вращения,  - угловое ускорение цилиндра,
- угловое ускорение цилиндра,  - его радиус.
- его радиус.
Условие отсутствия проскальзывания ( ) приводит к уравнению
) приводит к уравнению
|
|
|
 .
.
Решая систему записанных уравнений, найдем ускорение цилиндра
 .
.
 7.7. Однородный сплошной цилиндр массы m и радиуса R (рис.61) в момент t = 0 начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти угловое ускорение цилиндра.
7.7. Однородный сплошной цилиндр массы m и радиуса R (рис.61) в момент t = 0 начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти угловое ускорение цилиндра.
Решение. Направим ось X вертикально вниз вдоль движения цилиндра, а ось Z - перпендикулярно плоскости чертежа, проходящей через центр масс цилиндра (значок  на рис.61). Цилиндр совершает плоское движение – поступательное движение вдоль оси X и вращательное вокруг оси Z. Покажем силы, действующие на цилиндр при его движении вниз, это сила тяжести
на рис.61). Цилиндр совершает плоское движение – поступательное движение вдоль оси X и вращательное вокруг оси Z. Покажем силы, действующие на цилиндр при его движении вниз, это сила тяжести  и сила натяжения нити
и сила натяжения нити 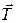 . Запишем систему уравнений, описывающих движение цилиндра. Уравнение поступательного движения цилиндра в проекциях на ось X
. Запишем систему уравнений, описывающих движение цилиндра. Уравнение поступательного движения цилиндра в проекциях на ось X
 ,
,
где a - ускорение центра масс цилиндра.
Уравнение вращательного движения цилиндра относительно оси Z
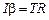
где  - момент инерции цилиндра относительно оси вращения,
- момент инерции цилиндра относительно оси вращения,  – угловое ускорение цилиндра,
– угловое ускорение цилиндра,  - его радиус.
- его радиус.
Нить не проскальзывает, поэтому соотношение между кинематическими параметрами
 .
.
Решив совместно записанные уравнения, получим угловое ускорение цилиндра:
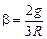 .
.
7.8. Однородное кольцо радиуса R раскрутили до угловой скорости  и осторожно положили на горизонтальную плоскость. Сколько времени кольцо будет вращаться на плоскости, если коэффициент трения равен
и осторожно положили на горизонтальную плоскость. Сколько времени кольцо будет вращаться на плоскости, если коэффициент трения равен  .
.
 Решение. Направим ось Z перпендикулярно горизонтальной плоскости, на которую положили кольцо (рис.62). Уравнение вращательного движения кольца относительно оси Z:
Решение. Направим ось Z перпендикулярно горизонтальной плоскости, на которую положили кольцо (рис.62). Уравнение вращательного движения кольца относительно оси Z:
 .
.
Выделим на кольце малый элемент массой 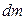 и найдем момент силы трения этого элемента относительно оси Z:
и найдем момент силы трения этого элемента относительно оси Z:
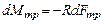 .
.
Тогда момент силы трения кольца относительно этой оси равен
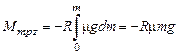 .
.
Учитывая, что момент инерции кольца относительно оси Z равен  , уравнение вращательного движения примет вид:
, уравнение вращательного движения примет вид:
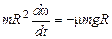 ,
,
 .
.
В момент остановки кольца его угловая скорость равна нулю 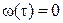 , поэтому, проинтегрировав левую часть уравнения от
, поэтому, проинтегрировав левую часть уравнения от  до 0, а правую от 0 до
до 0, а правую от 0 до  , получим
, получим
 ,
,
откуда выразим искомую величину:
 .
.
|
|
|


