Статический расчет подстропильной фермы

♦ Расчетный пролет и нагрузки. Подстропильная ферма загру­жена реакциями двух стропильных ферм, опирающихся на ее нижний пояс, и плитами покрытия, опирающихся на ее верхний пояс (по ребру от 4-х плит, т.е. нагрузка от одной плиты покрытия).

Расчетный пролет фермы l ₀ = L - 2а ₀= 12 - 2 · 0,15 = 11,7 м (а ₀ = 150 мм - расстояние от разбивочной оси до точки приложения опорной ре­акции подстропильной фермы). Масса фермы по табл. 2.3 равна 11,3 т, а вес - 11,3 · 9,81 = 110,8 кН, тогда погонная нагрузка от собственного веса:

при γ_f = 1 g_nw = 110,8 · 0,95 / 12 = 8,77 кН/м;

при γ_f > 1 g_w = 8,77 · 1,1 = 9,65кН/м.

Сосредоточенная сила F ₁, передающаяся непосредственно на верх­ний пояс фермы от плит покрытия:

при γ_f = 1

F _{1 n} = 3 · 6 · (g _{1 n} + S_n) = 3 · 6 · (2,544 + 0,95) = 62,89 кН,

в т.ч. от постоянной и временной длительной

F _{1 n, l} = 3 · 6 · (2,544 + 0,3 · 0,95) = 50,92 кН;

при > 1

F ₁= 3 · 6 · (g ₁ + s) = 3 · 6 · (3,0 + 1,33) = 77,94 кН.

 

 

Рис. 6.29. Опалубочные размеры подстропильной фермы L = 12 м

 

Величины распределенных постоянных нагрузок от покрытия и снеговой нагрузки приняты по табл. 2.4 настоящего пособия.

Средний узел нижнего пояса подстропильной фермы загружен не­симметрично, так как опорные реакции стропильных ферм смежных проле­тов различны по величине и их равнодействующая создает крутящий мо­мент в этом узле. В проектной практике это обстоятельство часто учитыва­ется эквивалентным увеличением равнодействующих сил R ₁и R ₂

(6.7)

где коэффициент α зависит от величины эксцентриситета е ₀равнодейст­вующей сил R ₁ и R ₂:при е ₀ = 0; 5; 10 и 15 см коэффициент α принимает зна­чения соответственно 1; 0,87; 0,67 и 0,5.

В данном примере сосредоточенные силы R ₁и R ₂:

при γ_f = 1

R _{1 n} = [(2,544 + 0,95) · 6 · 18 + 58,9 · 0,95 - 62,89] / 2 = 185,21 кН;

R _{2 n} = [(2,544 + 0,95) · 6 · 24 + 90,3 · 0,95 - 62,89] / 2 = 263,02 кН;

в т.ч. от продолжительно действующих нагрузок

R _{1 n, l} = [(2,544 + 0,3 · 0,95) · 6 · 18 + 58,9 · 0,95 - 62,89] / 2 = 149,3 кН;

R _{2 n, l} = [(2,544 + 0,3 · 0,95) · 6 · 24 + 90,3 · 0,95 - 62,89] / 2 = 215,14 кН;

при γ_f > 1

R ₁ = [(3 + 1,33) · 6 · 18 + 58,9 · 1,1 · 0,95 - 77,94] / 2 = 225,57 кН;

R ₂ = [(3 + 1,33) · 6 · 24 + 90,3 · 1,1 · 0,95 - 77,94] / 2 = 319,97 кН.

Силы R₁ и R₂ приложены в узле с эксцентриситетом относительно оси нижнего пояса е ₁ = е ₂ = е = 0,135 м. Тогда эксцентриситет равнодействующей сил R ₁и R ₂из условия равновесия

По линейной интерполяции находим коэффициент α = 0,94. Тогда приведенная сосредоточенная сила на средний узел нижнего пояса под­стропильной фермы

при γ_f = 1

в т.ч. от продолжительно действующей части нагрузки

при γ_f > 1

Нагрузку от собственного веса подстропильной фермы и от плит покрытия, опирающихся непосредственно на ее верхний пояс, также при­водим к узловой:

при γ_f = 1

F _{3 n} = g_nw(l ₁ + l ₂ ) / 2 + F _{1 n} / 2 = 8,77 · (3,98 + 4,0) / 2 + 62,89 / 2 = 66,44 кН; в т.ч. от продолжительно действующей части нагрузки

F _{3 n, l} = 8,77 · (3,98 + 4,0) / 2 + 50,92 / 2 = 60,45 кН;

при γ_f > 1

F₃ = 9,65 · (3,98 + 4,0) / 2 + 77,94 / 2 = 77,47 кН.

Опорные реакции подстропильной фермы:

при γ_f = 1

R_{A, n} = F _{2 n} / 2 + F _{3 n} = 476,84 / 2 + 66,44 = 304,86 кН;

в т.ч. от продолжительно действующей части нагрузки

R_{A, l} = F _{2 n, l} / 2 + F _{3 n, l} = 387,7 / 2 + 60,45 = 254,3 кН;

при γ_f > 1

R_A = F ₂ / 2 + F ₃ = 580,41 / 2 + 77,47 = 367,65 кН.

♦ Определение усилий в элементах фермы. В принятой расчет­ной схеме фермы (рис. 6.30) жесткие узлы условно заменены шарнирными. Поскольку верхний пояс загружен внеузловой нагрузкой F ₁, то, кроме нор­мальных усилий, в нем возникнут изгибающие моменты. Для определения нормальных усилий всю нагрузку, в т.ч. и внеузловую, приводим к узловой и прикладываем в узлы верхнего пояса. Определение нормальных усилий в элементах фермы выполним методом вырезания узлов (табл. 6.12).

 

 

Рис. 6.30. К расчету подстропильной фермы: а - расчетная схема;

б - к определению усилий в стержнях

 

Углы между стержнями фермы:

tg α ₁ = 1,95 / 3,85 = 0,5064; α ₁ = 26° 51';

tg =1,95 / 2 = 0,975; α ₂ = 44° 16';

sin α ₁ = 0,4517; cos α ₁ = 0,892;

sin α ₂= 0,698; cos α ₂= 0,716.

Вычислим изгибающие моменты в стержнях верхнего пояса от за­гружения его внеузловой нагрузкой F ₁ для чего воспользуемся методикой, изложенной в книге Жемочкина Б.Н. "Расчет рам".

 

Таблица 6.12

 

Значения жесткостей стержней, сходящихся в узле С, приведены в табл. 6.13.

Момент в заделке i - го стержня, примыкающего к узлу:

M_i = β ₁ · M_sup, (6.8)

где β ₁- коэффициент, зависящий от соотношения погонных жесткостей рассматриваемых стержней;

M_sup - опорный момент в стержне 3-6 с заделанными концами.

При i_i / i_m ≥4 коэффициент β ₁ = 0,1, а при i_i / i_m ≤1 - β₁ = 0,2. Здесь i_m - погонная жесткость среднего из всех сходящихся в узле стержней; i_i - средняя погонная жесткость всех стержней, исключая средний.

 

Таблица 6.13

 

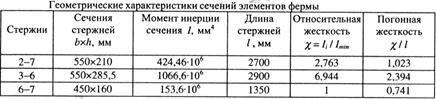
Средняя погонная жесткость стержней 2-7 и 3-6:

i_i = (i _2-7 + i _3-6) /2 = (1,023 + 2,394) / 2 = 1,709; i_m = i _6-7 = 0,741;

i_i / i_m = 1,709 / 0,741 = 2,306 > 1.

По интерполяции находим

Опорные моменты в стержне 3-6 при условии жесткой заделки стержня в узел С:

М ^С _3-6 = F₁l / 8 = - 77,94 · 2,9 / 8 = - 28,25 кНм;

М ^С _6-7 = β₁М ^С _3-6 = - 0,123 · 28,25 = - 3,48 кНм.

Опорный момент в стержне 2-7:

i_i / i_m = (2,394 + 0,741) / 2 = 1,568 > 1;

М _2-7 = - 0,181 · 28,25 = - 5,11кНм.

Из условия равновесия узла С

М_3-6 = М ^С _3-6 - М ^С _6-7 - М ^С _2-7 = 28,25 - 3,48 - 5,11 = 19,66 кНм.

Тогда момент в середине пролета стержня 3-6

M_{l/ 2}= F ₁ l / 4 - М _3-6 = 77,94 · 2,9 / 4 - 19,66 = 36,85 кНм.

6.6.3. Расчет сечений элементов фермы по I-й группе предель­ных состояний

♦ Нижний пояс. Наибольшее растягивающее усилие при коэффи­циенте γ_f > 1 равно N ≈ 726 кН и действует в стержне 7-1. Требуемая пло­щадь сечения арматурных канатов

где γ_{s 6}= 1,15 для арматурных канатов класса К-7 [3, п. 3.7]. Требуемое количество канатов п = A_sp / f_s = 574 / 90,6 = 6,34 шт. Принимаем 7 Ø12 К-7 (A_sp = 634 мм²).

♦ Верхний пояс. Стержень 2-7. Сечение стержня b x h = 550х210 мм; а = а′ = 30 мм; h ₀ = h - a = 210 - 30=180 мм. Усилия от всех нагрузок при γ_f > 1:

N = N _2-7 = 813,92 кH; М = М _2-7 = 5,11 кНм;

в т.ч. от продолжительных нагрузок:

При e₀ = M / N= 5,11 / 813,92 = 6,3 · 10^-3 м < 0,125 h = 0,125 · 0,21 = 0,026 м расчетная длина стержня 2-7 в плоскости фермы по табл. 24 [5] составляет l ₀ = 0,9 l = 0,9 · 2700 = 2430 мм. Случайные эксцентриситеты составляют: е_а1 = l ₀ / 600 = 2430 / 600 = 4,05 мм; е_{а 2} = h / 30 = 210 / 30 = 7 мм; е_а3 = 10 мм. Так как проектный эксцентриситет е ₀ = 6,3 мм < е_а3 = 10 мм, принимаем е ₀= е_а3 = 10 мм.

Принимаем симметричное армирование верхнего пояса и опреде­ляем требуемую площадь сечения продольной арматуры. При l ₀ / h = 2430 / 210 ≈ ≈ 12 > 10 необходим учет гибкости стержня, для чего определим условную критическую силу и коэффициент увеличения начального экс­центриситета.

1. M ₁= М + 0,5 N · (h ₀ -а′) = 5,11 + 0,5 · 813,92 · (0,18-0,03) = 66,15 кНм.

2. М _{1 l} = M_l + 0,5 N_l · (h ₀ - а′) = 4,26 + 0,5 · 679 · (0,18 - 0,03) = 55,2 кНм.

3. φ_l = 1 + βM _{1 l} / M ₁= 1 + 1 · 55,2 / 66,15 = 1,834 < 1 + β = 2.

4. δ_е = е ₀ / h = 10 / 210 = 0,048.

5. δ_{е, min} = 0,5 - 0,01 l ₀ / h- 0,01 R_b = 0,5 - 0,01 · 12 - 0,01 · 17,55 = 0,204.

6. δ_е = 0,048 < δ_{е, min} = 0,204, принимаем δ_е = δ_{е, min} = 0,204.

7. α_s = E_s / E_b = 2 · 10⁵ / 34500 = 5,8; µ = 0,01 (первое приближение).

Условная критическая сила

Коэффициент увеличения начального эксцентриситета

тогда расчетный эксцентриситет

е = η · е ₀ + 0,5 h - а′ = 1,193 · 10 + 0,5 · 210 - 30 ≈ 87 мм.

Вспомогательные расчетные параметры:

1.

где ω =0,85 - 0,008 R_b = 0,85 - 0,008 · 17,55 = 0,71; σ_sR = R_s = 365 МПа.

2.

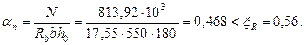
3.

4. δ = a' / h₀ = 30 / 180 = 0,167.

Требуемая площадь сечения симметричной продольной арматуры

при α_n < ξ_R

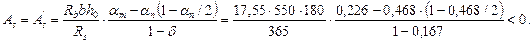
Так как по расчету арматура не нужна, принимаем ее по конструк­тивным требованиям

A_S = A_S' = A_{s, min} = 0,002 bh ₀= 0,002 · 550 · 180 = 198 мм².

Принимаем у широких граней стержня по 3 Ø14 А-III (A_s = A_S′ = 462 мм²) с тем, чтобы расстояния между продольными стержнями не превышали 400 мм. Коэффициент армирования

µ = (A_s + A_s′) / bh ₀ = 2 · 462 / (550 · 180) = 0,0093

близок к первоначально принятому значению µ = 0,01.

Стержень 3-6. Сечение стержня в середине панели b х h = 550х300 мм, а = а′ = 30 мм; h ₀ = 300 - 30 = 270 мм. Усилия от всех на­грузок при коэффициенте γ_f > 1: N = 1023,7 кН; М = 37,89 кНм; в т.ч. от про­должительных нагрузок: N_l = 701 · 1023,7 / 846,6=847,6 кН; М_l =36,85 · 847,6/1023,7=30,51 кНм.

При е ₀= М / N = 36,85 / 1023,7 = 0,036м < 0,125 h = 0,125 · 0,3 = 0,0375 м расчетная длина стержня 3-6 в плоскости фермы составляет l ₀ =0,9 l =0,9 · 2900 = = 2610 мм = 2,61 м. Поскольку l ₀ / h = 2610 / 300 = 8,7 < 10, гибкость не учитываем, т.е. коэффициент η = 1. Тогда расчетный эксцентриситет

е = η · е₀ + 0,5 h - а′ = 1 · 36 + 0,5 · 300 - 30 = 156 мм.

Вспомогательные расчетные параметры:

δ = 30 / 270 = 0,393.

Требуемая площадь сечения симметричной продольной арматуры

при α_n = 0,392 < ξ_R = 0,56

т.е. по расчету арматура не требуется. Из конструктивных соображений принимаем у широких граней стержня по 3 Ø14 А-III (A_s =A_s′ =462 мм² > А_{s , min} = = 0,002 · 550 · 270 = 297 мм²). Поперечные стержни можно принять Ø6 A-I с шагом 150 мм.

♦ Раскос 6-7. Сечение раскоса b x h = 450x160 мм; а = а′ = 25 мм; h₀ = 160 - 25 = 135 мм. При действии растягивающего усилия N = 415,73 кН и изгибающего момента М = 3,48 кНм раскос испытывает внецентренное растяжение. Расчетные эксцентриситеты продольной силы:

е= 0,5 h – M / N - а= 0,5 · 160 - 3,48 · 10⁶ / 415,73 · 10³ - 25 = 47 мм;

е' = 0,5 h + М / N - а= 0,5 · 160 + 3,48 · 10⁶ / 415,73 · 10³ - 25 = 63 мм.

При е' = 63 мм < (h ₀ - а) = 135 - 25 = 110 мм требуемая площадь сечения продольной арматуры:

Сечение ненапрягаемой арматуры растянутого раскоса 6-7 должно обеспечивать не только его прочность, но и требуемую трещиностойкость. Поэтому из условий ограничения ширины раскрытия нормальных трещин принимаем симметричную арматуру по 6 Ø12 А-III (A_s = A_s′ = 678 мм²), ко­торые располагаем у широких граней раскоса; поперечные стержни также принимаем Ø6 A-I с шагом 150 мм.

 

6.6.4. Расчет сечений элементов фермы по II-й группе предель­ных состояний

 

♦ Расчет по трещиностойкости нижнего пояса. Наибольшее растягивающее усилие от всех нагрузок с коэффициентом γ_f = 1 действует в панели 7-1 и равно N_n = N _7-1 ≈ 602 кН. Начальное предварительное напряжение принимаем σ_sp = 0,9 R_{s, ser} = 0,9 · 1335 ≈ 1200 МПа. Коэффициент точности натяжения γ_sp = 1 - ∆ γ_sp = 1 – 0,1 = 0,9 (∆ γ_sp = 0,1 при механическом способе на­тяжения).

Вычисляем потери предварительного напряжения.

Первые потери

 

От релаксации напряжений в натянутой арматуре

σ ₁= 0,1 σ_sp – 20 = 0,1 · 1200 - 20 = 100 МПа.

От перепада температур между арматурой и натяжными устройст­вами

σ ₂= 1,25 ∆t = 1,25 · 65 = 81,25 МПа.

От деформации анкеров, расположенных у натяжных устройств:

σ ₃= (∆l / l) · E_s = (2 / 13000) · 18 · 10⁴ = 27,7 МПа,

где ∆l = 2 мм [4, табл. 4].

Напряжение в арматуре с учетом вычисленных потерь

σ_{sp 1}= σ_sp - σ ₁ - σ ₂ - σ ₃ = 1200 - 100 - 81,25 - 27,7 = 991 МПа.

Усилие в арматуре A_sp с учетом вычисленных потерь

Р ₀= σ_{sp 1} A_sp = 991 · 634 = 628294 Н.

Напряжение в бетоне на уровне центра тяжести напрягаемой арма­туры при ее симметричном расположении в сечении нижнего пояса (A_sp′ = A_sp и е _{0 р} = 0)

σ_bp = P ₀ / A_red = 628294 / 118803 = 5,29 МПа,

где A_red = bh + α_spA_sp = 550 · 210 + 5,21 · 634 = 118803 мм².

Коэффициент α = 0,25 + 0,025 R_bp = 0,25 + 0,025 · 20 = 0,75 < 0,8.

Потери от быстронатекающей ползучести при уровне напряжений

σ_bp / R_bp = 5,29 / 20 = 0,264 < α = 0,75

σ ₆ = 34 σ_bp / R_bp = 34 · 0,264 = 9,0 МПа.

Итого первые потери:

σ_{l 1} = σ ₁ + σ ₂ + σ ₃ + σ ₆ = 100 + 81,25 + 27,7 + 9 = 218 МПа.

Усилие обжатия с учетом первых потерь

P ₁ = (σ_sp - σ_{l 1}) A_sp = (1200 - 218) · 634 = 622588 Н.

Вторые потери

 

Потери от усадки бетона σ ₈ = 35 МПа [4, поз.8 табл. 4].

Напряжения в бетоне на уровне центра тяжести сечения с учетом первых потерь

σ_{bp 1}= P ₁ / A_red = 622588 / 118803 = 5,24 МПа.

Потери от ползучести при σ_{bp 1} / R_bp = 5,24 / 20 = 0,262 < α = 0,75

σ ₉ = 128 σ_{bp 1} / R_bp = 128 · 0,262 = 33,54 МПа.

Итого вторые потери σ_{l 2} = σ ₈ + σ ₉ = 35 + 33,54 = 68,54 МПа.

Полные потери σ_l = σ_{l 1} + σ_{l 2} = 218 + 68,54 = 286,54 МПа.

Усилие обжатия с учетом всех потерь и коэффициентом точности на­тяжения γ_sp = 1

P ₂ = (σ_sp - σ_l) A_sp = (1200 - 286,54) · 634 = 579133 H.

Усилие трещинообразования в нижнем поясе

N_crc = R_{bt, ser}A + Р ₂ = 1,95 · 550 · 210 + 579133 = 804358 Н ≈ 804 кН.

Так как N_crc = 804 кН > N_n = 602 кН, трещины в нижнем поясе не образуются.

♦ Расчет по раскрытию трещин раскоса 6-7. Усилия от нагру­зок при γ_f = 1:

N_n = 341,58кН; N_l = 277,73 кН; М_п = (341,58 / 415,73) · 3,48 = 2,86 кНм; M_l = 2,86 · (277,73 / 341,58) = 2,33 кНм.

Так как продолжительно действующие нагрузки составляют более 80% полной нагрузки, проверяем только продолжительное раскрытие трещин от усилий N_l и M_l.

1. h ₀ = 160 - 25 = 135 мм;

2. e ₀ = M_l / N_l = 2,33 · 10⁶ / 277,73 · 10³ = 8,4 мм.

3. e_x = h / 2 - а- е ₀ = 160 / 2 - 25 - 8,4 = 46,6 мм.

При е ₀= 8,4 мм < 0,8 h = 0,8 · 160 = 128 мм продольная сила при­ложена в пределах расстояния z_s = h ₀- a ' = 135 - 25 = 110 мм, тогда напряжения в растянутой арматуре согласно п. 4.9 [5]

 

 

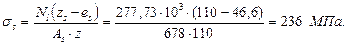
5. Коэффициент армирования сечения

 

 

где h ₀₁ = h ₀ - e_s = 135 - 46,6 = 88,4 мм [5, п. 4.7].

6. φ_l = 1,6 - 15 = 1,6 - 15 · 0,017 = 1,345.

7. Ширина продолжительного раскрытия трещин

где δ = 1,2 - для растянутых элементов;

η = 1 - для арматуры класса А-III.

Следовательно, трещиностойкость раскоса 6-7 обеспечена.

 

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: