Расчетный пролет и нагрузки

Расчетный пролет арки l ₀ = l - 2 а = 35,9 - 2 · 0,15 = 35,6 м,

где а = 0,15 м - расстояние между осями опор арки (от ее торца до оси опирания на колонну).

Нормативные и расчетные постоянные нагрузки от покрытия на ар­ку с учетом коэффициента надежности по назначению γ_п = 0,95 приняты по табл. 2.4 данного пособия.

Расчетная постоянная нагрузка на 1 м с учетом собственного веса арки G_п = 400 кH

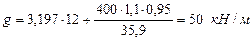
Расчетная снеговая для III-го района нагрузка на 1 м

s =1,4 · 12 · 0,95 ≈ 16кН/м.

При расчете считаем ось арки очерченной по квадратной параболе, хотя из соображений унификации блоков и стыков между ними принимаем ее очерченной по дуге окружности. Вследствие пологости арки разница между тем и другим очертаниями оси несущественна.

 

Геометрические характеристики оси арки

 

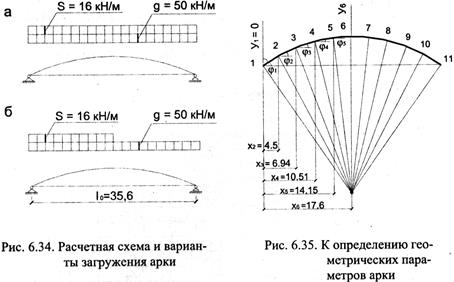
Расчетная схема арки и ее загружения приведены на рис. 6.34.

Стрелу подъема арки назначаем равной f = l ₀ / 9 = 35,6 / 9 = 3,96 м, тогда основные геометрические характеристики оси круговой арки:

радиус оси -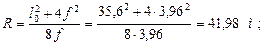

 

центральный угол -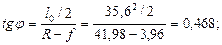

длина оси арки - S = 2 R · α₀ = 2 · 41,98 · 0,436 = 36,6 м,

где

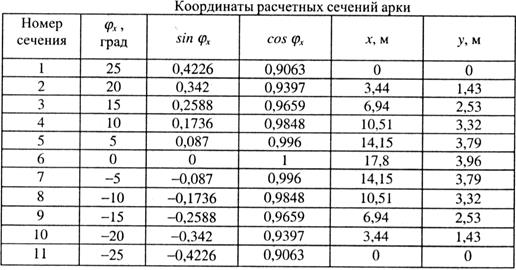
Арку разбиваем на 10 равных частей (дуге 0,1 части соответствует угол φ ₁/ 5 = 25° / 5 = 5°) и определяем координаты сечений (рис. 6.35) по формулам:

x = l ₀ / 2 - R · sinφ; y = R · cosφ - a, (6.10)

где а = R – f = 41,98 - 3,96 = 38,02 м.

 

 

Например:

при φ ₁ = 25° (sin 25° = 0,4226; cos 25° = 0,9063):

x ₁ = 35,6 / 2 - 41,98 · 0,4226 = 0,059 ≈ 0; у ₁ = 41,98 · 0,9063 - 38,02 = 0,026 ≈ 0;

при φ₂ = 20° (sin 20° = 0,342; cos 20° = 0,9397):

x ₂= 35,6 / 2 - 41,98 · 0,342 = 3,44 м; у ₂ = 41,98 · 0,9397 - 38,02 = 1,428 м ≈ 1,43м.

Остальные координаты x и у определены аналогично и приведены в табл. 6.14; координата у ₆соответствует стреле подъема f.

Как отмечалось в п. 6.7, продольные деформации арки, снижающие распор, учитывают коэффициентом податливости k < 1. Для его вычисле­ния по формуле (6.9) необходимо задаться содержанием арматуры в сече­ниях арки и затяжки.

Принимаем в первом приближении для арки

A_s = A_s′ = 0,015 A_b = 0,015 · (2 · 500 · 80 + 2 · 60 · 210 + 840 · 80) ≈ ≈ 2600мм²,

тогда при α = E_s / Е_b = 2 · 10⁵ / 29 · 10³ = 6,9 получим:

- площадь приведенного сечения арки

A_red = A_b + α (A_s + A _s′)= 172400 + 6,9 · 2 · 2600 = 20,83 · 10⁴ мм²;

- расстояние до центра тяжести приведенного сечения

у ₀ = h / 2 = 1000 / 2 = 500 мм;

- момент инерции приведенного сечения

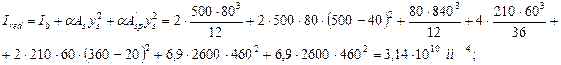в т.ч. I_b = 2,38 · 10¹⁰ мм⁴;

 

Таблица 6.14

 

- радиус инерции приведенного сечения

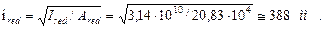
Сечение арматуры затяжки в первом приближении

А_{s 1} = 0,01 A ₁ = 0,01 · 440 · 440 ≈ 2000 мм²,

тогда площадь приведенного сечения затяжки

A_{red 1} = 440 · 440 + 6,9 · 2000 = 20,74 · 10⁴ мм².

Коэффициент податливости по формуле (6.9)

 

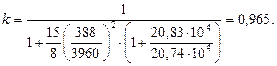
6.8.4. Определение усилий от единичной нагрузки q = 1

 

Распор от равномерно распределенной по пролету арки единичной нагрузки q = 1 кН/м

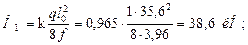
то же от равномерно распределенной нагрузки на половине пролета

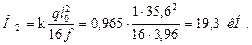
Балочные моменты М ₀и поперечные силы Q ₀определяются по следующим формулам:

- при загружении всего пролета

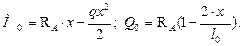
где 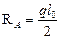- опорная балочная реакция;

- при загружении половины пролета усилия в незагруженной части

M ₀ = R_b x; Q ₀ = R_b,

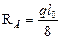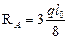где и при загружении левой половины пролета.

Усилия в сечениях арки определяем по формулам:

М_х = М ₀- Ну; (6.11)

N_x = Q ₀ · sinφ + H · cosφ; (6.12)

Q_x = Q ₀ · cosφ - H · sinφ, (6.13)

где φ - угол между касательной к оси арки и горизонталью (табл. 6.14).

В табл. 6.15 и 6.16 приведены усилия в сечениях арки соответст­венно от единичной нагрузки по всему пролету и на половине пролета, вы­численные по формулам (6.11) - (6.13). Полные усилия в сечениях арки по­лучим умножением соответствующих величин усилий из табл. 6.15 и 6.16 на масштабные коэффициенты, равные:

для постоянной нагрузки k ₁ = g / q = 50 /1 = 50;

для временной нагрузки k ₂ = s / q = 16/1 = 16.

Величины расчетных усилий в сечениях арки и распора для рас­смотренных схем загружения приведены в табл. 6.17.

 

 

Таблица 6.15

 

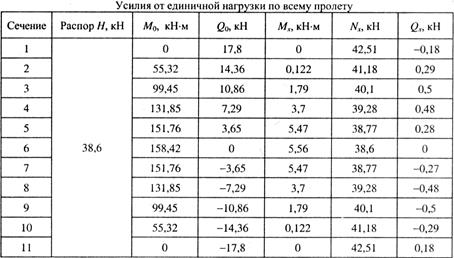
Таблица 6.16

 

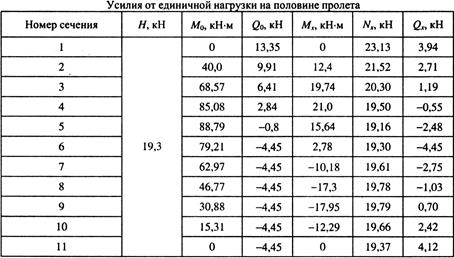
Таблица 6.17

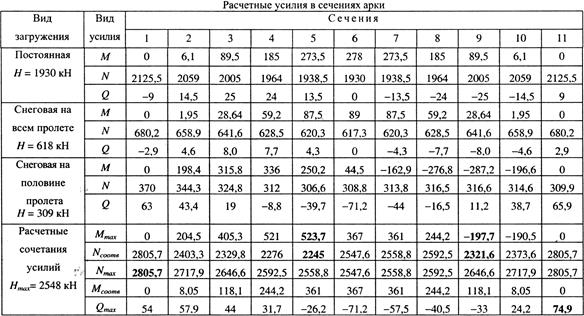
Расчет затяжки

 

♦ Расчет по прочности. Арматуру затяжки подбираем как для центрально растянутого элемента

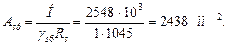
Здесь коэффициент γ_s6 не учитывается, так как проволоки в сече­нии располагаются попарно вплотную без зазоров [4, п. 3.7].

Требуемое число проволок п= 2438 / 19,6 = 124 шт. Проволоки располагаем попарно симметрично по сечению через 50 мм, тогда общее число проволок п= 2 · 8 · 8 = 128 шт. с площадью A_sp = 128 · 19,6 ≈ 2509 мм².

♦ Определение потерь предварительного напряжения. Величину начального предварительного напряжения принимаем максимально допус­тимой по п. 1.15 [4], т.е. σ_sp = 0,95 R_{s, ser} = 0,95 · 1255 = 1192 МПа ≈ 1190 МПа.

Первые потери:

- от релаксации напряжений

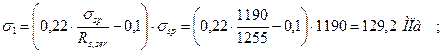
- от температурного перепада

σ ₂= 1,25∆t = 1,25 · 65 = 81,25 МПа;

- от деформации анкеров при инвентарных зажимах

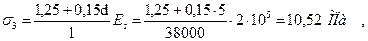
где l ≈ 38 м - длина проволоки (расстояние между гранями упоров);

- σ ₄ = 0 - напрягаемая арматура не имеет перегибов;

- σ ₅ = 0 - натяжение производится на упоры стенда;

- от быстронатекающей ползучести: σ_{sp 0}= σ_sp - σ ₁ - σ ₂ - σ ₃ = 1190 - 129,2 - - 81,25 - 10,52 ≈ 969 МПа; P ₀= σ_{sp 0} · A_sp = 969 · 2509 = 2431221 Н ≈ 2431 кН; σ_sp = Р ₀ / А_{red 1}= 2431 · 10³ / /20,74 · 10⁴ = 11,72 МПа; α = 0,25 + 0,025 R_bp = 0,25 + + 0,025 · 21 = 0,775 < 0,8, σ_bp / R_bp = 11,72 / /21= 0,558 < α = 0,775;

σ ₆ = 34 σ_bp / R_bp = 34 · 0,558 = 19 МПа.

Итого первые потери σ_{l 1} = σ ₁ + σ ₂ + σ ₃ + σ ₄ + σ ₅ + σ ₆ = 129,2 + 81,25 + 10,52 + 19 = 240 МПа.

Вторые потери:

- от усадки тяжелого бетона класса В30 σ ₈ = 35 МПа;

- от ползучести: σ_{sp 1} = 1190 - 240 = 950 МПа; Р ₁ = σ_{sp 1} A_sp = 950 · 2509 = 2383550 Н; σ_{bp 1}= 2383550 / 20,74 · 10⁴ = 11,49 МПа;

σ_{bp 1} / R_bp = 11,49 / 21 = 0,547 < 0,75; σ ₉ = 128 σ_{bp 1} / R_bp = 128 · 0,547 = 70МПа.

Итого вторые потери: σ_{l 2} = 35 + 70 = 105 МПа.

Полные потери: σ_{l 1} + σ_{l 2} = 240 + 105 = 345 МПа > 100 МПа

Напряжение в арматуре с учетом всех потерь

σ_{sp 2}= σ_sp - (σ_{l 1} + σ_{l 2})= 1190 - 345 = 845МПа.

Усилие обжатия с учетом всех потерь при γ_sp = 1

Р ₂= σ_{sp 2} A_sp = 845 · 2509 = 2120105 Н = 2120 кН.

♦ Расчет по образованию трещин. Величина распора при значении коэффициента надежности по нагрузке γ_f = 1 составляет

Н_{n, max} = H_max / γ_f = 2548 / 1,2 = 2123 кН,

где γ_f = 1,2 - усредненное значение коэффициента надежности.

Усилие образования трещин при γ_sp = 1 [4, табл. 2] и A_s = 0

N_crc = R_{bt, ser} (А + 2αA_sp) + γ_spP ₂= 1,8 · (19,36 · 10⁴ + 2 · 6,9 · 2509) + 1 · 2120 · · 10³ = 2530803 Н = 2531 кН. Так как H_{n, max} = 2123 кH < N_crc = 2531 кН, трещины в затяжке не образуются.

♦ Проверка прочности бетонного сечения затяжки в стадии обжатия. В этой стадии затяжку можно рассматривать как центрально сжатый неармированный элемент при действии продольной силы N_p, пред­ставляющей усилие обжатия. Численное значение этой силы определим согласно п. 3.44 а [4]

N_p = (σ_{sp 1} - 330) А_sp = (1045 - 330) · 2509 = 1794000 Н = 1794 кН,

где σ_{sp 1}= (σ_sp - σ_{l 1}) · γ_sp = (1190 - 240) · 1,1 = 1045 МПа.

Условие прочности

N_p= 1794kH < N_u = A · R^p_b = 19,36 · 10⁴ · 12,1 = 2342 кН

выполняется, т.е. прочность бетонного сечения затяжки при обжатии обес­печена.

 

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: