 |
Изменение возбуждения. V-oбразные кривые.
|
|
|
|
Рассмотрим параллельную работу генератора с сетью очень большой мощности при изменении тока в его обмотке возбуждения.
Допустим, что после включения генератора на параллельную работу он работает вхолостую и его э.д.с  уравновешивает напряжение сети
уравновешивает напряжение сети 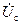 ; тогда в его статорной обмотке не будет никакого тока. Если теперь увеличить ток в обмотке возбуждения (перевозбудить машину), то напряжение сети
; тогда в его статорной обмотке не будет никакого тока. Если теперь увеличить ток в обмотке возбуждения (перевозбудить машину), то напряжение сети 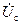 не будет уравновешивать э.д.с.
не будет уравновешивать э.д.с.  , появится избыток э.д.с.
, появится избыток э.д.с. 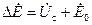 (рис. 4-65).
(рис. 4-65).
Избыточная э.д.с.  вызовет ток в обмотках всех параллельно работающих машин. Его можно принять равным
вызовет ток в обмотках всех параллельно работающих машин. Его можно принять равным 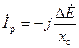 , так как сопротивлением. Обмоток всех других машин можно пренебречь, как и активным сопротивлением рассматриваемой машины. Угол θ при этом не изменится (θ = 0).
, так как сопротивлением. Обмоток всех других машин можно пренебречь, как и активным сопротивлением рассматриваемой машины. Угол θ при этом не изменится (θ = 0).
Ток 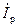 есть реактивный ток. Он будет отставать от
есть реактивный ток. Он будет отставать от  , а следовательно, и от напряжения генератора U г на
, а следовательно, и от напряжения генератора U г на 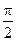 , как это показано на рис. 4-65. Этот ток будет тем больше, чем больше машина перевозбуждена и чем меньше сопротивление x c.
, как это показано на рис. 4-65. Этот ток будет тем больше, чем больше машина перевозбуждена и чем меньше сопротивление x c.
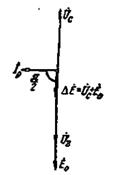
Рис. 4-65. Перевозбуждение машины.
При уменьшении тока возбуждения (при недовозбуждении) напряжение сети 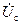 будет больше э.д.с. (рис. 4-66). Следовательно, в цепи обмоток параллельно работающих машин будет действовать э.д.с.
будет больше э.д.с. (рис. 4-66). Следовательно, в цепи обмоток параллельно работающих машин будет действовать э.д.с. 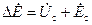 , которая также создает реактивный ток
, которая также создает реактивный ток 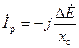 , но теперь этот ток будет опережать напряжение генератора на
, но теперь этот ток будет опережать напряжение генератора на 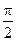 , как показано на рис. 4-66.
, как показано на рис. 4-66.
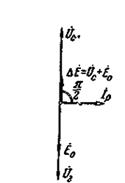
Рис. 4-66. Недовозбуждение машины.
К тому же самому мы придем, если учтем выводы, полученные нами из рассмотрения реакции якоря в синхронном генераторе (§ 4-3,а).
Так как результирующий поток в машине, как мы выяснили, при U c = const должен быть постоянным, то при перевозбуждении реакция якоря должна быть размагничивающей. Такую реакцию якоря в генераторе создает отстающий ток. Следовательно, при перевозбуждении генератор работает с отстающим током.
|
|
|
При недовозбуждении для сохранения результирующего потока неизменным реакция якоря должна быть намагничивающей. А такую реакцию якоря создает опережающий ток. Следовательно, при недовозбуждении генератор работает с опережающим током.
То же самое будем иметь при изменении возбуждения генератора, работающего с нагрузкой.
На рис. 4-67 представлена диаграмма генератора, работающего с различными токами и cos φ, но при постоянном напряжении и постоянной мощности, отдаваемой в сеть.
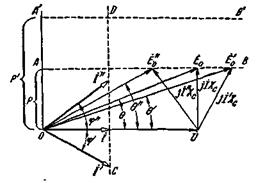
Рис. 4-67. Диаграммы генератора при различных возбуждениях (при U = const и Р = const).
Рассмотрим сначала работу генератора стоком I и cos φ = l. Проекция  на линию 0 А, перпендикулярную к
на линию 0 А, перпендикулярную к  , равна
, равна 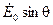 . Следовательно, эта проекция при постоянных напряжении U и синхронном сопротивлении х с может служить мерой мощности машины, равной
. Следовательно, эта проекция при постоянных напряжении U и синхронном сопротивлении х с может служить мерой мощности машины, равной 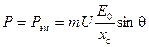 .
.
Если при постоянной мощности (Р = Р эм = const) изменить возбуждение, то изменится э.д.с. Е 0, но ее проекция на линию, перпендикулярную к U, при этом должна остаться неизменной. Таким образом, при изменении возбуждения конец вектора э.д.с.  будет скользить по прямой АВ.
будет скользить по прямой АВ.
Из рис. 4-67 следует, что при перевозбуждении 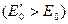 генератор работает с отстающим током, а при недовозбуждении
генератор работает с отстающим током, а при недовозбуждении 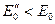 ) — с опережающим током.
) — с опережающим током.
Ток  всегда направлен под углом
всегда направлен под углом 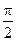 к
к 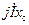 . Конец вектора
. Конец вектора  при изменении возбуждения будет скользить по прямой CD, так как активная составляющая тока cos φ = const.
при изменении возбуждения будет скользить по прямой CD, так как активная составляющая тока cos φ = const.
Переход от одного установившегося режима к другому при изменении возбуждения протекает следующим образом (рис. 4-67). Допустим, например, что э.д.с. E 0 увеличивается до 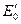 . Угол θ не может измениться столь же быстро до θ' вследствие инерции вращающихся частей. Увеличение Е 0 при том же значении угла θ вызовет увеличение электромагнитной мощности, которая в течение некоторого промежутка времени будет больше мощности на валу. Поэтому ротор должен замедлить свое вращение. Угол θ при этом должен уменьшаться. После нескольких затухающих колебаний получается установившийся режим работы при новых значениях
. Угол θ не может измениться столь же быстро до θ' вследствие инерции вращающихся частей. Увеличение Е 0 при том же значении угла θ вызовет увеличение электромагнитной мощности, которая в течение некоторого промежутка времени будет больше мощности на валу. Поэтому ротор должен замедлить свое вращение. Угол θ при этом должен уменьшаться. После нескольких затухающих колебаний получается установившийся режим работы при новых значениях 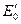 и θ', при которых электромагнитная мощность снова соответствует мощности на валу.
и θ', при которых электромагнитная мощность снова соответствует мощности на валу.
|
|
|
В течение переходного процесса, связанного с небольшим изменением угловой частоты ротора, регуляторы частоты первичных двигателей обычно не успевают подействовать, так как их чувствительность относительно невелика.
Следовательно, изменение возбуждения вызовет лишь изменение реактивной составляющей тока.
Для изменения активной составляющей тока или активной мощности, отдаваемой в сеть, необходимо изменить мощность, создаваемую первичным двигателем. Например, для увеличения мощности с Р до Р ' нужно соответственно увеличить мощность на валу машины. Тогда вектор Е 0  при изменении возбуждения будет скользить по линии А ' В ' (рис. 4-67). Линии AВ, А ' В ', параллельные вектору
при изменении возбуждения будет скользить по линии А ' В ' (рис. 4-67). Линии AВ, А ' В ', параллельные вектору  , называются линиями постоянной мощности синхронного генератора.
, называются линиями постоянной мощности синхронного генератора.
Опытным путем можно найти зависимости тока статора от тока возбуждения I = f (I в) при U = const и Р = const. Соответствующие кривые для различных значений Р показаны на рис. 4-68.
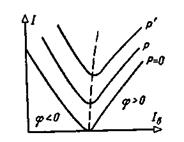
Рис. 4-68. V -образные кривые генератора.
Вследствие их сходства с латинской буквой V они называются V -образными кривыми. На рис. 4-68 видно, что для каждой мощности существует такое возбуждение, при котором ток статора синхронного генератора будет минимальным. Этому току соответствует cosφ = l. На рис. 4-68 кривая минимальных токов показана пунктиром. Она, очевидно, представляет собой регулировочную характеристику при cosφ = l.
V -образные кривые могут быть также найдены при помощи векторных диаграмм, для построения которых должны быть известны характеристика холостого хода и параметры машины.
4-7.3. Параллельная работа двух соизмеримых по мощности генераторов
Рассмотрим параллельную работу генераторов, имеющих одинаковые номинальные величины и одинаковые параметры. Будем считать, что их общая нагрузка определяется двумя векторами U и I, показанными на рис. 4-69.
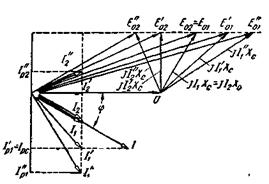
Рис. 4-69. К параллельной работе генераторов одинаковой мощности (изменение возбуждения).
|
|
|
Допустим, что мощности, подведенные к генераторам со стороны их первичных двигателей, равны между собой и во время работы остаются постоянными и что общее напряжение U также поддерживается постоянным.
Если э.д.с. первого и второго генераторов равны друг другу: 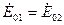 , то они будут работать с одинаковыми токами
, то они будут работать с одинаковыми токами 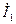 и
и 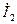 . При этом их cos φ равны между собой и в то же время равны cos φ общей нагрузки. Оба генератора, следовательно, работают с одинаковыми активной и реактивной мощностями.
. При этом их cos φ равны между собой и в то же время равны cos φ общей нагрузки. Оба генератора, следовательно, работают с одинаковыми активной и реактивной мощностями.
Пусть теперь возбуждение первого генератора стало больше, а второго меньше. На рис. 4-69 показано, что при этом cos φ генераторов изменятся, так же, как и токи. Первый генератор, имеющий э.д.с. 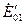 будет работать с низким cos φ, а второй генератор, имеющий э.д.с.
будет работать с низким cos φ, а второй генератор, имеющий э.д.с. 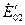 , будет работать с cos φ = 1. Следовательно, всю необходимую для внешней сети реактивную мощность будет вырабатывать только первый генератор (
, будет работать с cos φ = 1. Следовательно, всю необходимую для внешней сети реактивную мощность будет вырабатывать только первый генератор (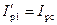 ).
).
При дальнейшем увеличении э.д.с. первого генератора до 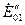 и уменьшении э.д.с. второго генератора до
и уменьшении э.д.с. второго генератора до 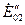 токи их будут
токи их будут 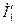 и
и 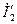 . В этом случае cos φ первого генератора станет еще меньше, тогда как cos φ второго генератора будет соответствовать опережающему току. Первый генератор будет доставлять реактивный ток (или реактивную мощность) не только сети, но и второму генератору, работающему с недовозбуждением.
. В этом случае cos φ первого генератора станет еще меньше, тогда как cos φ второго генератора будет соответствовать опережающему току. Первый генератор будет доставлять реактивный ток (или реактивную мощность) не только сети, но и второму генератору, работающему с недовозбуждением.
Таким образом, улучшение cos φ одного из генераторов влечет за собой ухудшение cos φ другого генератора. Путем изменения возбуждения можно как угодно распределять реактивную мощность между параллельно работающими синхронными машинами.
Ранее было показано, что изменение возбуждения параллельно работающих генераторов влечет за собой изменение их реактивных токов, тогда как их активные токи остаются неизменными соответственно практически неизменным механическим мощностям первичных двигателей.
Для изменения нагрузки генератора, т. е. отдаваемой им активной мощности, необходимо воздействовать на первичный двигатель, чтобы создаваемый им вращающий момент, приложенный к валу генератора, изменился. Предположим, что мы увеличили момент на валу одного из генераторов; тогда ротор его забежит несколько вперед, угол θ возрастет и генератор будет работать с большей нагрузкой. Если при этом общая нагрузка сети остается постоянной и если необходимо иметь неизменной частоту тока, то увеличение нагрузки первого генератора должно сопровождаться одновременным уменьшением нагрузки второго генератора. Последнее достигается также путем соответствующего воздействия на его первичный двигатель.
|
|
|
Следовательно, для перевода нагрузки с одного генератора на другой необходимо мощность на валу одного генератора уменьшать, а на валу второго — увеличивать. Если при этом требуется сохранить прежнее напряжение, то нужно одновременно воздействовать и на возбуждение обоих генераторов.
Обратимся к рис. 4-70, который иллюстрирует процесс перевода нагрузки с одного генератора на другой.
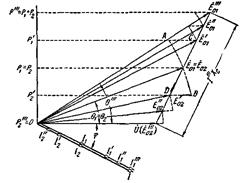
Рис. 4-70. К параллельной работе генераторов одинаковой мощности (перевод нагрузки с одного генератора на другой).
Допустим, что вначале генераторы имеют одинаковые э.д.с. и токи как активные, так и реактивные (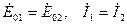 ). Увеличим вращающий момент на валу первого генератора; тогда вектор
). Увеличим вращающий момент на валу первого генератора; тогда вектор 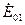 отклонится несколько влево соответственно увеличению угла θ1 (точка А). Вращающий момент на валу второго генератора уменьшим; тогда вектор э.д.с.
отклонится несколько влево соответственно увеличению угла θ1 (точка А). Вращающий момент на валу второго генератора уменьшим; тогда вектор э.д.с. 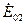 отклонится вправо соответственно уменьшению угла θ2 (точка В). Далее нужно сделать одинаковыми cos φ генераторов. Для этот необходимо увеличить возбуждение первого генератора, чтобы конец вектора э.д.с.
отклонится вправо соответственно уменьшению угла θ2 (точка В). Далее нужно сделать одинаковыми cos φ генераторов. Для этот необходимо увеличить возбуждение первого генератора, чтобы конец вектора э.д.с. 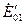 , переместился в точку С, и уменьшить возбуждение второго генератора, чтобы конец вектора э.д.с.
, переместился в точку С, и уменьшить возбуждение второго генератора, чтобы конец вектора э.д.с. 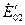 переместился в точку D. При этом
переместился в точку D. При этом 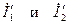 будут совпадать по фазе.
будут совпадать по фазе.
Дальнейшее должно быть понятным из рис. 4-70. Зигзагообразная линия вверх от 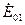 соответствует движению вектора э.д.с. первого генератора. Зигзагообразная линия вниз от
соответствует движению вектора э.д.с. первого генератора. Зигзагообразная линия вниз от 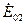 соответствует движению вектора э.д.с. второго генератора. При
соответствует движению вектора э.д.с. второго генератора. При 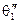 и
и 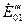 всю нагрузку несет только первый генератор. Напряжение при этом сохраняет свое начальное значение. При
всю нагрузку несет только первый генератор. Напряжение при этом сохраняет свое начальное значение. При 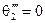 и
и 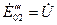 второй генератор не несет никакой нагрузки, ток в его статорной обмотке
второй генератор не несет никакой нагрузки, ток в его статорной обмотке 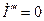 . Следовательно, отключение второго генератора от общих шин не вызовет никаких нежелательных явлений, так как при этом не будет резкого изменения режима работы первого генератора.
. Следовательно, отключение второго генератора от общих шин не вызовет никаких нежелательных явлений, так как при этом не будет резкого изменения режима работы первого генератора.
4-7.4. Электромагнитная и синхронизирующая мощности явнополюсной машины
В предыдущем при определении электромагнитной и синхронизирующей мощностей мы исходили из упрощенной диаграммы, не учитывающей ни насыщения машины, ни различия магнитных проводимостей по ее продольной и поперечной осям.
Найдем теперь выражения для Р эм и P c явнополюсной машины с учетом различия ее параметров по продольной и поперечной осям. При этом будем также пренебрегать активным сопротивлением обмотки статора и насыщением магнитной цепи машины.
|
|
|
Обратимся к видоизмененной диаграмме явнополюсной машины, представленной на рис. 4-71.
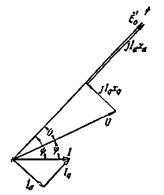
Рис. 4-71. Видоизмененная диаграмма явнополюсной машины.
Из этой диаграммы имеем:
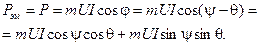
Имея в виду, что
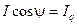 и
и  ,
,
из рис. 4-71 найдем:
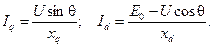
Подставляя найденные значения в уравнение для Р эм, после преобразований получим:
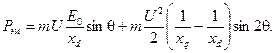 (4-75)
(4-75)
Полученное выражение для электромагнитной мощности явнополюсной машины показывает, что эта мощность зависит не только от возбуждения, но и от различия хd и xq.
Из (4-75) следует, что явнополюсная машина может работать без возбуждения, т. е. при E 0=0. В этом случае она называется реактивной машиной, работа которой будет рассмотрена в последующем (§ 4-10).
Разделив (4-75) на синхронную угловую скорость, получим уравнение для электромагнитного вращающего момента, развиваемого явнополюсной машиной:
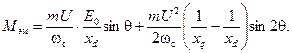 (4-76)
(4-76)
Второй член правой части этого уравнения равен так называемому реактивному моменту:
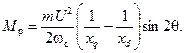 (4-77)
(4-77)
Равенства (4-75) и (4-76), очевидно, применимы и для неявнополюсной машины. Для этой машины xq можно считать равным xd, поэтому равенство (4-75) будет точно такое же,
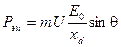 , (4-78)
, (4-78)
как и ранее полученное равенство (4-69), где х c = хd.
В соответствии с (4-75) на рис. 4-72 построена кривая, выражающая зависимость Р эм от угла θ, т. е. угловая характеристика явнополюсного генератора.
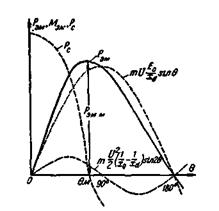
Рис. 4-72. Угловая характеристика явнополюсной машины.
Продифференцировав равенство (4-75) по углу θ, получим выражение для удельной синхронизирующей мощности явнополюсной машины:
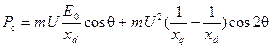 . (4-79)
. (4-79)
Кривая P c = f (θ) также показана на рис. 4-72.
По предложению проф. Г.Н. Петрова угловую характеристику и максимальную электромагнитную мощность Р эм можно определить с учетом насыщения и активного сопротивления обмотки якоря следующим образом: надо построить несколько регулировочных характеристик I в = f (I) при U = const и cos φ = const для различных cos φ и кривые θ = f (I) при тех же условиях; затем соответственно номинальному току возбуждения I в.н = const провести линию, параллельную оси абсцисс; тогда точки пересечения этой линии с указанными кривыми дают величины, необходимые для построения угловой характеристики (регулировочные характеристики и кривые θ = f (I) для различных cos φ должны быть построены при помощи векторных диаграмм и характеристики холостого хода).
4-7.5. Статическая перегружаемость синхронной машины
Статическая перегружаемость S синхронной машины, так же как и предел ее статической устойчивости, определяется отношением
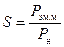 . (4-80)
. (4-80)
Это отношение представляет собой долевое значение максимальной электромагнитной мощности при U н и I в.н, которое для неявнополюсной машины можно выразить при помощи равенства (4-78) следующим образом:

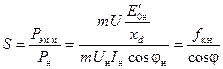 , (4-81)
, (4-81)
где 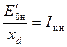 и
и  — кратность тока короткого замыкания при номинальном возбуждении (
— кратность тока короткого замыкания при номинальном возбуждении (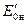 — э.д.с. по спрямленной характеристике холостого хода при I в.н) или
— э.д.с. по спрямленной характеристике холостого хода при I в.н) или
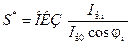 , (4-82)
, (4-82)
где ОКЗ = f к0 — кратность тока короткого замыкания при возбуждении холостого хода (см. § 4-3, а). (Согласно ГОСТ 533-51 на “Генераторы электрические паротурбинные двухполюсные (турбогенераторы)" S не должна быть ниже 1,7.)
Полученное выражение, которое обычно используется при практических расчетах, является приближенным, потому что оно было выведено без учета активного сопротивления обмотки статора и насыщения магнитной цепи машины.
Активным сопротивлением обмотки статора в обычных случаях можно пренебречь, так как оно оказывает ничтожное влияние на P эм.м. Насыщение магнитной цепи в небольшой степени влияет на P эм.м, повышая его значение на несколько процентов и увеличивая угол θ, соответствующий Р эм.м до 100 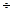 110°.
110°.
Если не учитывать насыщения, то Р эм.м явнополюсной машины, как следует из рис. 4-72, получается при θм < 90°. Значение θм найдем, приравняв нулю первую производную от Р эм по θ, т. е. приравняв нулю P с.
Введем обозначения:
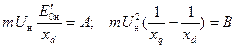 .
.
Тогда получим из (4-79):
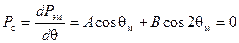 ,
,
откуда
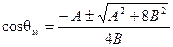 . (4-83)
. (4-83)
Подставляя в (4-75) полученное значение θм, найдем Р эм.м, а следовательно, согласно (4-80) статическую перегружаемость S.
Статическая перегружаемость S синхронной машины, так же как и предел ее статической устойчивости, определяется отношением
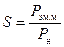 . (4-80)
. (4-80)
Это отношение представляет собой долевое значение максимальной электромагнитной мощности при U н и I в.н, которое для неявнополюсной машины можно выразить при помощи равенства (4-78) следующим образом:

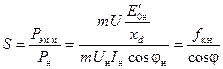 , (4-81)
, (4-81)
где 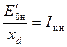 и
и  — кратность тока короткого замыкания при номинальном возбуждении (
— кратность тока короткого замыкания при номинальном возбуждении (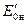 — э.д.с. по спрямленной характеристике холостого хода при I в.н) или
— э.д.с. по спрямленной характеристике холостого хода при I в.н) или
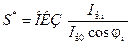 , (4-82)
, (4-82)
где ОКЗ = f к0 — кратность тока короткого замыкания при возбуждении холостого хода (см. § 4-3, а). (Согласно ГОСТ 533-51 на “Генераторы электрические паротурбинные двухполюсные (турбогенераторы)" S не должна быть ниже 1,7.)
Полученное выражение, которое обычно используется при практических расчетах, является приближенным, потому что оно было выведено без учета активного сопротивления обмотки статора и насыщения магнитной цепи машины.
Активным сопротивлением обмотки статора в обычных случаях можно пренебречь, так как оно оказывает ничтожное влияние на P эм.м. Насыщение магнитной цепи в небольшой степени влияет на P эм.м, повышая его значение на несколько процентов и увеличивая угол θ, соответствующий Р эм.м до 100 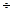 110°.
110°.
Если не учитывать насыщения, то Р эм.м явнополюсной машины, как следует из рис. 4-72, получается при θм < 90°. Значение θм найдем, приравняв нулю первую производную от Р эм по θ, т. е. приравняв нулю P с.
Введем обозначения:
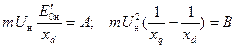 .
.
Тогда получим из (4-79):
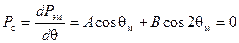 ,
,
откуда
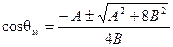 . (4-83)
. (4-83)
Подставляя в (4-75) полученное значение θм, найдем Р эм.м, а следовательно, согласно (4-80) статическую перегружаемость S.
Статическая перегружаемость S синхронной машины, так же как и предел ее статической устойчивости, определяется отношением
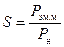 . (4-80)
. (4-80)
Это отношение представляет собой долевое значение максимальной электромагнитной мощности при U н и I в.н, которое для неявнополюсной машины можно выразить при помощи равенства (4-78) следующим образом:

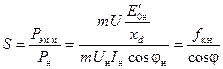 , (4-81)
, (4-81)
где 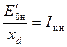 и
и  — кратность тока короткого замыкания при номинальном возбуждении (
— кратность тока короткого замыкания при номинальном возбуждении (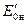 — э.д.с. по спрямленной характеристике холостого хода при I в.н) или
— э.д.с. по спрямленной характеристике холостого хода при I в.н) или
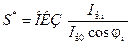 , (4-82)
, (4-82)
где ОКЗ = f к0 — кратность тока короткого замыкания при возбуждении холостого хода (см. § 4-3, а). (Согласно ГОСТ 533-51 на “Генераторы электрические паротурбинные двухполюсные (турбогенераторы)" S не должна быть ниже 1,7.)
Полученное выражение, которое обычно используется при практических расчетах, является приближенным, потому что оно было выведено без учета активного сопротивления обмотки статора и насыщения магнитной цепи машины.
Активным сопротивлением обмотки статора в обычных случаях можно пренебречь, так как оно оказывает ничтожное влияние на P эм.м. Насыщение магнитной цепи в небольшой степени влияет на P эм.м, повышая его значение на несколько процентов и увеличивая угол θ, соответствующий Р эм.м до 100  110°.
110°.
Если не учитывать насыщения, то Р эм.м явнополюсной машины, как следует из рис. 4-72, получается при θм < 90°. Значение θм найдем, приравняв нулю первую производную от Р эм по θ, т. е. приравняв нулю P с.
Введем обозначения:
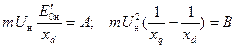 .
.
Тогда получим из (4-79):
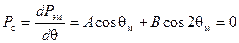 ,
,
откуда
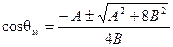 . (4-83)
. (4-83)
Подставляя в (4-75) полученное значение θм, найдем Р эм.м, а следовательно, согласно (4-80) статическую перегружаемость S.
4-8. Синхронный двигатель
|
|
|


