Алгоритмы циклической структуры

Часто при решении задач приходится многократно вычислять значение по одним и тем же алгоритмам. Такие многократно повторяемые алгоритмы называются циклами. Различают циклы с заданным и неизвестным числом повторений. К последним относятся итерационные циклы, характеризующиеся последовательным приближением к искомому значению с заданной точностью.

Для организации цикла необходимо выполнить следующие действия: 1) задать перед циклом начальное значение переменной, изменяющейся в цикле; 2) изменять переменную перед каждым новым повторением цикла; 3) проверять условие окончания или повторения цикла; 4) управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из него по окончании. Последние три функции выполняются многократно.

Переменная, изменяющаяся в цикле, называется параметром цикла.

1. Вычислить значения функции 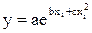, если Х задано массивом, состоящим из 40 элементов.

2. Вычислить и вывести на печать положительные значения функции у=sin (nx) ‑ cos (n/x) при n = 1, 2, …, 50.

3. Вычислить значения функции z = x^k/k, большие а, если k=1, 2, ….

4. Вычислить значения функции у = а³/(а² + х²) при х, изменяющемся от 0 до 3 с шагом 0,1.

5. Напечатать таблицу значений аргумента х и функции

у(х) = а³/(а² + х²) при значении х, изменяющихся от 0 до 3 с шагом 0,1.

6. Составить программу для вычисления значения функции у = 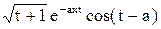при одновременном изменении аргументов t от 2 до 3 с шагом 0,2 и х от 1 до 2 для а = ‑2,1.

7. Составить программу вычисления n! (1 ^. 2 ^. 3 ^. 4^.... ^. n):

8. Составить программу, вычисляющую экстремальное значение функции 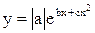при изменении аргумента х от 0 до 4 с шагом h.

9. Вычислить:

а) у = (2n ‑1)! = … 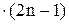, n >0;

б) у = (2n)! = 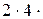… 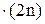, n >0;

в) у = n!, n > 0.

10. Вычислить: у = .

11. Определить, является ли заданное натуральное число со­вер­шен­ным, т.е. равным сумме всех своих делителей, кроме самого этого числа (на­­пример, число 6 совершенно: 6=1+2+3).

12. Дано целое n >2. Напечатать простые числа из диапазона [2, n].

13. Найти сумму цифр заданного натурального числа.

14. Вычислить k ‑ количество точек с целочисленными коорди­на­та­ми, попадающих в круг радиуса R (R>0) с центром в начале координат.

15. Напечатать в возрастающем порядке все трехзначные числа, в де­­сятичной записи которых нет одинаковых цифр.

16. Даны целое n и вещественные числа 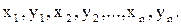Рассматривая пары как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.

17. Напечатать все простые делители натурального числа.

18. Уравнение (предложена М.В. Дякиным).

Дана последовательность 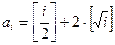, 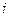‑ натуральное число. Квадратные скобки 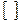обозначают в формуле взятие целой части (округление до ближайшего меньшего целого числа). Обозначим .

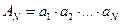Написать программу, которая для заданного натурального 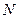решает уравнение ,

где 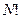- обозначение числа 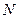- факториал: .

Программа должна найти и сообщить:

1) точное значение x в виде несократимой дроби;

2) сумму цифр числителя и сумму цифр знаменателя этой дроби.

Образец вывода результата:

Число 6, числитель дроби X=10, знаменатель дроби X=63.

Сумма цифр числителя =1, сумма цифр знаменателя =9.

19. Задача « Кучи и яма»(предложена А.Б. Дернятиным).

Имеются яма и несколько куч (не более пяти) кирпичей. Разре­шает­ся перекладывать кирпичи из куч в яму по следующему правилу: если коли­чество кирпичей в куче больше, чем в яме, то можно переложить столько кирпичей, сколько находится в яме в данный момент. Требуется разработать алгоритм, который позволяет уложить в яму как можно боль­ше кирпичей.

Образец вывода результатов:

К1=150001 К2=81234 Я=70000 было

К1=150001 К2=11234 Я=140000 в яму из кучи 2‑й

К1=10001 К2=11234 Я=280000 в яму из кучи 1‑й

20. Представления натурального числа (предложена Д.Я.Шараевым).

Известно, что любое натуральное число N (0<N 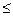1000) может быть пред­­ста­вле­но в виде суммы квадратов не более четырех поло­жи­тель­ных целых чисел. Составьте программу, которая в ответ на ввод числа N вы­водит ко­ли­чество S всех различных представлений этого числа. Пред­­став­ления, отличающиеся лишь порядком слагаемых, считаются одинаковыми.

Пример. N=4. S=2. (1²+1²+1²+1²=4, 2²=4)

21. Задача «Многоугольник»(предложена Н.Ю. Лукояновым).

На плоскости декартовыми координатами своих вершин дан вы­пук­лый -угольник. Его вершины пронумерованы от 1 до n в порядке следо­ва­ния против часовой стрелки. Задан номер 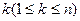. Требуется провести че­рез 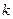-вершину -угольника два луча (назовем их a и b) так, чтобы эти лучи делили -угольник на три равновеликие по площади части.

Входные данные: - число вершин; (х₁, y₁), (x₂, y₂), …, (x_n, y_n) - координаты 1-й, 2-й, и т.д. -й вершины соответственно; 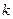- номер выделенной вершины.

Выходные величины: координаты (х_а, y_a) и (x_b, y_b) точек пересечения лучей a и b с границей -угольника.

 

Алгоритмы работы с рядами

При работе с рядами обычно составляют рекуррентную формулу, которая задает значение i+1-го члена ряда (Y(i+1)) через значения пре­ды­ду­щих членов, чаще ‑ i-го члена ряда (Y(i)). Обычно используют отношение i+1-го чле­на к i-му члену, подставляют их значения, и после преоб­ра­зо­ва­ний полу­чает­ся рекуррентная формула.

Пример. Вычислить значение членов бесконечного ряда 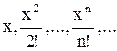точностью до члена 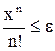. Считать, что требуемая точ­ность (ε) достигнута, если очередное слагаемое по модулю меньше ука­зан­ной точности и все последующие слагаемые можно уже не учитывать. Опре­де­лим рекуррентную формулу Y(i+1)/Y(i)=(x⁽ⁱ⁺¹⁾/(i+1)!)/(xⁱ/i!)=x/i. Получим рекуррентную формулу Y(i+1)=Y(i)*x/(i+1).

1. Вычислить сумму членов для следующих рядов с точностью до 10^-4:

а)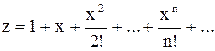

б)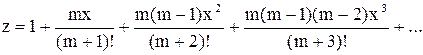

Для вычисления текущего значения члена ряда использовать рекуррентную формулу , где n ‑ номер члена ряда. Начальное значение у принять равным ;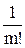

в) ;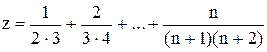

г) ;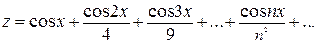

д) ;.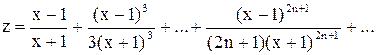

е) ;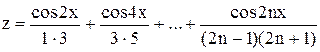

ж) .

Текущий член ряда вычислять, используя рекуррентную формулу.

2. Составить программу вычисления значений членов убывающей последовательности … с точностью до10^-4.

3. Составить программу вычисления членов бесконечного ряда

z =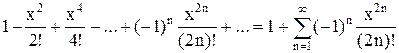

с точностью до10^-4.

4. Не используя стандартные функции (за исключением abs), вычислить с точностью до 10^-4:

а)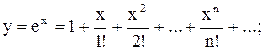

б)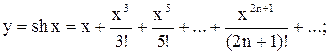

в)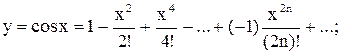

г)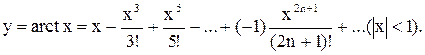

5. Вычисление f = 10!

6. Вычислить:

а) у = cos(x)+ cos(x²) + cos(x³) +…+cos(x³⁰);

б) у = 1! + 2! + 3! + …+ n! (n>1);

 

в) у ‑ первое из чисел sin(x), sin(sin(x)), sin(sin(sin(x,…))), меньшее по модулю 10^-4.

7. Числа Фибоначчи («f_n») определяются по формулами f₀ = f₁ = 1;

f_n = f_n-1 + f_n-2 при n = 2, 3, …:

а) определить четвертое число Фибоначчи;

б) вычислить первое число Фибоначчи, большее m (m > 1);

в) вычислить s ‑ сумму всех чисел Фибоначчи, которые не превосходят 1000.

⇐ Предыдущая64656667686970717273Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: