Задание к лабораторной работе

Разработать программу, реализующую оба описанных метода для функции 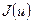; найти её минимальное значение на отрезке [-100,100].

Варианты заданий

№ вар.				№ вар.
			-0.85			-0.3	3.5
		-0.65		-0.1	4.0
		-0.45		0.2	4.5
		-0.25		0.4	5.0
		-0.05		0.8	5.5
		0.15			0.2	-4.0
		0.35		0.4	-3.4
		0.55		0.6	-2.8
		0.75		0.8	-2.2
		0.95		1.0	-1.6
		-1.5	1.0		1.2	-1.0
	-1.3	1.5		1.4	-0.4
	-1.1	2.0		1.6	-0.2
	-0.9	2.5		1.8	0.8
	-0.7	3.0		2.0	1.4

 

Контрольные вопросы

1. Дайте определение унимодальной функции.

2. Каким образом в методе дихотомии гарантируется попадание точки минимума 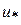в отрезок при любом ?

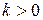3. Чем отличается метод дихотомии от метода золотого сечения?

4. Почему в методе золотого сечения, начиная со второй итерации, необходимо вычислять только один раз значение функции вместо двух в методе дихотомии?

5. Какой из рассмотренных в лабораторной работе методов сходится быстрее и почему?

 

Лабораторная работа №2. Метод ломаных

Конечной целью любой практической задачи оптимизации, как правило, является определение глобального на данном множестве экстремума функции. Большинство же методов минимизации функции одной переменной позволяют найти лишь один из локальных минимумов функции. Одним из немногих методов нахождения глобального экстремума функции одной переменной на отрезке является метод ломаных.

Постановка задачи

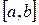Найти при помощи метода ломаных точку глобального минимума функции на отрезке . Найти минимальное значение функции.

Теоретическая часть

Метод ломанных применим для функций , удовлетворяющих условию Липшица на отрезке .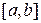

Опр. 1. Функция удовлетворяет условию Липшица (такие функции называют «липшицевыми») на отрезке 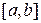, если существует такое число , называемое константой Липшица, что для него выполняется условие:

, (1)

Теперь рассмотрим собственно сам метод.

Будем предполагать, что константа Липшица известна.

Возьмем произвольную точку ; например, можно взять:

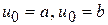или .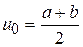

Построим функции , .

Определим точку исходя из условия . Нулевая итерация завершена.

На следующей итерации построим функцию , затем - функцию 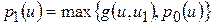, и, наконец, определим новую точку 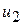, исходя из условия .

Рассмотрим 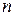-ю итерацию. К её началу известна последовательность точек . В этом случае построим функцию и определим следующую точку , исходя из условия .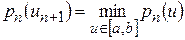

Примечание. Легко доказывается, что функции , , представляют собой ломанные линии, удовлетворяющие неравенствам:

,

.

Это означает, что ломаная линия по мере увеличения числа 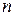приближается к функции снизу.

Итерации выполняются до тех пор, пока не будет достигнута заданная точность , см. следующий раздел «Сходимость и оценка погрешности метода».

Сходимость и оценка погрешности метода

Метод ломаных сходится, что утверждается в следующей теореме.

Теорема 1. Пусть - произвольная функция, удовлетворяющая на 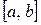условию (1). Тогда последовательность 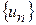, полученная с помощью метода ломаных такова, что:

1) , (2)

причем справедлива оценка

(3)

2) 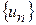сходится к множеству точек минимума на 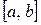, т.е. .

Оценка константы Липшица

Для применения метода ломаных необходимо знать константу Липшица функции . Для её оценки можно воспользоваться следующим алгоритмом.

Разобьем отрезок 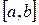на m подотрезков:

Обозначим

Несложно доказать, что для последовательности , справедливы следующие утверждения:

.

Следовательно, при достаточно большом m в качестве приближенного значения константы Липшица можно взять величину .

Примечание. Заниженная оценка константы Липшица может привести к неправильному нахождению минимального значения и точки минимума функции.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: