 |
Лабораторная работа №5. Метод покоординатного спуска
|
|
|
|
Постановка задачи
Требуется решить задачу оптимизации:
, (1)
где 
, 
, 
- заданные числа.
Теоретическая часть
Алгоритм
Будем использовать набор векторов: 
, с 
-й координатой, равной 1, 
.
Пусть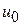 
- начальное приближение, 
- параметр метода. Допустим, что уже известны 
.
Пусть 
, где 
, 
(2)
Здесь 
- целая часть от 
.
Соотношения (2) обеспечивают циклический перебор координатных векторов 
.
Пусть 
, тогда если
(3)
то 
(4)
Иначе 
. Если
(5)
то 
(6)
Назовем 
итерацию удачной, если выполнилось хотя бы одно из условий (3) или (5). Если итерация неудачна, то определим
(7)
Здесь 
, 
- параметр метода.
Соотношения (7) означают, что если при переборе всех направлений (координатных осей ) с шагом 
реализовалась хотя бы одна удачная итерация, то не дробится и сохраняется, по крайней мере, в течение следующего цикла из n итераций.
Сходимость метода и оценка погрешности
Теорема 1. Пусть функция 
выпукла на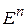 
и принадлежит классу 
, а начальное приближение 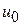таково, что множество 
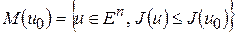- ограничено. Тогда последовательность 
, получаемая описанным методом, минимизирует на 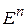и сходится к множеству 
, причем справедлива следующая оценка погрешности:
(8)
Задание к лабораторной работе
Разработать программу, реализующую метод покоординатного спуска для функции 
(значения 
, 
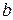, c, d определяются вариантами заданий) и 
, 
, 
. Программа должна выводить: координаты точки минимума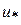 
; значение функции в данной точке 
; количество итераций, после которых достигается точность 
.
Варианты заданий
| № вар. |
|
| 
| 
| № вар. |
|
|
|
|
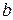
| -1.4 | 0.01 | 0.11 | 0.0 | 1.99 | 0.26 | ||||
| -1.3 | 0.04 | 0.12 | 0.1 | 2.56 | 0.27 | ||||
| -1.2 | 0.02 | 0.13 | 0.2 | 2.89 | 0.28 | ||||
| -1.1 | 0.16 | 0.14 | 0.3 | 3.24 | 0.29 | ||||
| -1.0 | 0.25 | 0.15 | 0.4 | 3.81 | 0.30 | ||||
| -0.9 | 0.36 | 0.16 | 0.5 | 4.00 | 0.31 | ||||
| -0.8 | 0.49 | 0.17 | 0.6 | 5.02 | 0.32 | ||||
| -0.7 | 0.64 | 0.18 | 0.7 | 4.84 | 0.33 | ||||
| -0.6 | 0.81 | 0.19 | 0.8 | 5.29 | 0.34 | ||||
| -0.5 | 0.94 | 0.20 | 0.9 | 5.76 | 0.35 | ||||
| -0.4 | 1.00 | 0.21 | 1.0 | 6.25 | 0.36 | ||||
| -0.3 | 1.21 | 0.22 | 1.1 | 6.76 | 0.37 | ||||
| -0.2 | 1.44 | 0.23 | 1.2 | 6.98 | 0.38 | ||||
| -0.1 | 1.69 | 0.24 | 1.3 | 7.29 | 0.39 | ||||
| 0.0 | 1.96 | 0.25 | 1.4 | 8.41 | 0.40 |
|
|
|
Лабораторная работа №6. Метод штрафных функций
Постановка задачи
Требуется решить задачу оптимизации:
, 
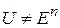(1)
Теоретическая часть
Алгоритм
В методе штрафных функций задача (1) сводится к последовательности задач минимизации:
(2)
где 
, 
- некоторая вспомогательная функция, причем, должна быть такой, что с ростом 
она мало отличается от на 
и быстро возрастает на 
. В качестве множества 
обычно выбирается множество простой структуры типа параллелепипеда или шара.
Опр. 1. Последовательность функций 
, определенных и неотрицательных на множестве , содержащем , называют штрафами или штрафными функциями множества на множестве , если
(3)
Так, если множество имеет вид
, (4)
то в качестве штрафных могут выбираться следующие функции:
(5)
или
, где (6)
;
.
Пусть , 
уже выбраны, определена на . В качестве функции будем брать:
. (7)
Будем считать, что
(8).
Если при каждом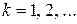 
нижняя граница достигается, то условия
(9)
определяют последовательность . Если же нижняя грань не достигается, то в качестве элементов последовательности будем брать точки 
, удовлетворяющие условиям:
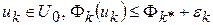, (10)
где 
для всех к и 
при 
.
Сходимость метода
Теорема 1. Пусть - замкнутое множество из 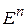функции 
полунепрерывны снизу на , 
. Пусть последовательность , которая определяется условиями (9), (10), имеет хотя бы одну предельную точку. Тогда все предельные точки принадлежат множеству точек минимума задачи (1), (4). Если, кроме того,
|
|
|
(11)
ограничено хотя бы при одном значении 
, то
(12)
Задание к лабораторной работе
Разработать программу, реализующую метод штрафных функций для минимизации функции 
(варианты функции определяются вариантами заданий к лабораторной работе № 4) на множестве 
, где 
. В качестве штрафной функции следует взять 
. Количество итераций должно быть таким, чтобы 
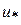Программа должна выводить координаты точки минимума , значение функции в данной точке 
и количество итераций.
Варианты заданий
| № вар. |
|
| № вар. |
|
|
| (1, 1) | -5 | (-4, 2) | |||
| (1, -1) | -3 | (5, 3) | |||
| (3, -2) | (-1, 2) | ||||
| (1, -1) | (2, -3) | ||||
| (3, 4) | -1 | (-2, 5) | |||
| (1, -1) | (3, 1) | ||||
| (1, 4) | (-3, 2) | -3 | |||
| (5, 2) | -1 | (1, -2) | |||
| (2, -1) | (-2, 1) | ||||
| (3, 1) | -4 | (1, -1) | |||
| (2, -1) | (2, 6) | ||||
| (7, 2) | (5, -1) | ||||
| (3, 1) | (1, -1) | ||||
| (1, 4) | (2, -1) | -1 | |||
| (2, -1) | (3, 5) | -2 |
Список литературы
1. Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 1980. – 552 с.
2. Бахвалов Н.С. Численные методы.Ч.1 – М.:Наука, 1973.
|
|
|
