 |
Сходимость и оценка погрешности метода
|
|
|
|
Сходимость метода будем рассматривать при следующих ограничениях на  :
:
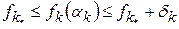 , где (6)
, где (6)
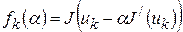 ;
;
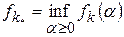

В этом случае справедлива теорема.
Теорема 1. Пусть 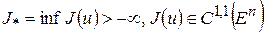 и
и  - выпукла на
- выпукла на 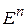 . Тогда для последовательности
. Тогда для последовательности  , определяемой условиями (3), (6), имеют место соотношения:
, определяемой условиями (3), (6), имеют место соотношения:
 (7)
(7)
Если, кроме того, в (6) 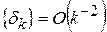 (
( ), то справедлива оценка:
), то справедлива оценка:
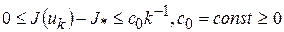 (8)
(8)
Следует заметить, что  , найденное по формуле (4), удовлетворяет (6) с
, найденное по формуле (4), удовлетворяет (6) с  .
.
Метод условного градиента
Алгоритм
Метод наискорейшего спуска не пригоден для нахождения минимального значения функции, если на задачу накладываются ограничения вида 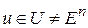 . Одной из модификаций градиентных методов, позволяющих решать подобные задачи, является метод условного градиента.
. Одной из модификаций градиентных методов, позволяющих решать подобные задачи, является метод условного градиента.
Он может быть использован для задач следующего вида:
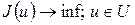 (9)
(9)
где  - выпуклое замкнутое ограниченное множество из
- выпуклое замкнутое ограниченное множество из 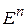 , функция
, функция  .
.
Опишем метод.
Пусть известно  -е приближение
-е приближение 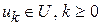 . Приращение функции
. Приращение функции  в точке
в точке  можно представить в виде
можно представить в виде
 .
.
Возьмем главную линейную часть этого приращения:
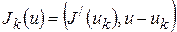 , (10)
, (10)
и определим вспомогательное приближение  из условий
из условий
 (11)
(11)
Так как множество  замкнуто и ограничено, а линейная функция
замкнуто и ограничено, а линейная функция  непрерывна, то точка
непрерывна, то точка  из (11) всегда существует. Если функция достигает своей нижней грани на
из (11) всегда существует. Если функция достигает своей нижней грани на  более чем в одной точке, то в качестве
более чем в одной точке, то в качестве  возьмем любую из них.
возьмем любую из них.
Рассмотрим в качестве примера нахождение точки  в случае, когда множество
в случае, когда множество  представляет собой
представляет собой 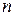 -мерный параллелепипед:
-мерный параллелепипед:
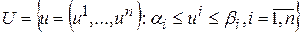 ,
,
В этом случае функция 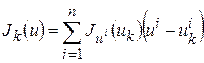 , или
, или 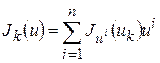 , очевидно достигает своей нижней грани на
, очевидно достигает своей нижней грани на 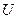 в точке
в точке  , где
, где
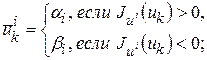
в случае 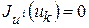 здесь возникает неопределенность, и в качестве
здесь возникает неопределенность, и в качестве 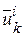 можно взять любое число на отрезке
можно взять любое число на отрезке  (иногда берут
(иногда берут 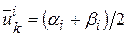 ).
).
В общем случае не всегда удается получить в явном виде вспомогательное приближение  . В таких ситуациях вместо (11) используются следующие условия:
. В таких ситуациях вместо (11) используются следующие условия:
|
|
|
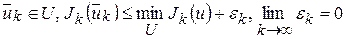 (12).
(12).
Допустим, что точка  , удовлетворяющая условиям (12) (или (11)), уже найдена. Тогда
, удовлетворяющая условиям (12) (или (11)), уже найдена. Тогда  -е приближение будем искать в виде
-е приближение будем искать в виде
 (13).
(13).
В силу выпуклости множества  всегда
всегда 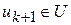 .
.
Если  (это может случиться, например, когда
(это может случиться, например, когда  ) имеем
) имеем  независимо от способа выбора
независимо от способа выбора  в (13). При определении
в (13). При определении  точно из условия (11) имеем:
точно из условия (11) имеем:
 или
или 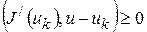
при всех 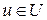 . Как известно, это означает, что точка
. Как известно, это означает, что точка  удовлетворяет необходимому условию минимума в задаче (9). Более того, если если
удовлетворяет необходимому условию минимума в задаче (9). Более того, если если  выпукла, то данное условие явлется и достаточным, т.е. в этом случае задача (9) решена.
выпукла, то данное условие явлется и достаточным, т.е. в этом случае задача (9) решена.
Теперь рассмотрим один из способов выбора шага  .
.
Данная величина может быть определена из следующих условий:
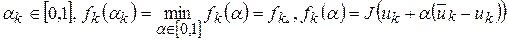 (14).
(14).
В частности, для функции
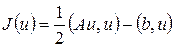 , (15)
, (15)
где 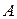 - симметричная положительно определенная матрица порядка
- симметричная положительно определенная матрица порядка 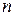 ,
, 
 , определяемая в соответствии с (15), вычисляется следующим образом. Вначале вычисляется промежуточная величина:
, определяемая в соответствии с (15), вычисляется следующим образом. Вначале вычисляется промежуточная величина:
 (16)
(16)
Затем находится искомое значение  :
:
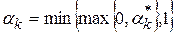
В качестве 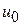 можно выбирать любую точку
можно выбирать любую точку 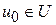 . В качестве критериев окончания счета можно использовать неравенства (5):
. В качестве критериев окончания счета можно использовать неравенства (5):
Метод условного градиента описан.
Сходимость метода и оценка погрешности
Метод условного градиента сходится с оценкой:
 (17)
(17)
Задание к лабораторной работе
Разработать программу нахождения минимума функции вида (2), завиящей от двух переменных, при помощи метода наискорейшего спуска и метода условного градиента. Для метода условного градиента в качестве множества  взять прямоугольник:
взять прямоугольник:
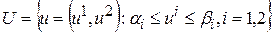 .
.
Программа должна предлагать пользователю меню, состоящее из трех элементов, первые два из которых позволяют выбрать один из рассмотренных методов, третий – «Выход». Предусмотреть ввод матрицы 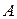 и вектора
и вектора 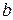 и проверку условия положительной определенности и симметричности матрицы
и проверку условия положительной определенности и симметричности матрицы 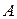 .
.
Начальная точка 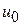 выбирается произвольно.
выбирается произвольно.
Результаты должны содержать: координаты точки минимума для функции  , минимальное значение функции и количество итераций.
, минимальное значение функции и количество итераций.
|
|
|
Варианты заданий
| № вар. | A, b, 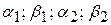
| № вар. | A, b, 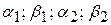
|
 , 0; 2; 3; 7 , 0; 2; 3; 7
| 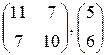 , 2; 4; 3; 4 , 2; 4; 3; 4
| ||
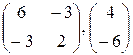 , 0; 2; 3 , 0; 2; 3
|  , -1; 1; 0; 2 , -1; 1; 0; 2
| ||
 , 1; 3; -4; -1 , 1; 3; -4; -1
|  , 0; 2; -4; -1 , 0; 2; -4; -1
| ||
 , 0; 5; 0; 3 , 0; 5; 0; 3
| 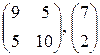 , 1; 3; -3; 1 , 1; 3; -3; 1
| ||
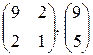 , 3; 7; 1; 4 , 3; 7; 1; 4
|  , 0; 2; 0; 2 , 0; 2; 0; 2
| ||
 -1; 1; 0; 2 -1; 1; 0; 2
| 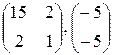 , -1; 0; -4; -2 , -1; 0; -4; -2
| ||
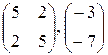 , 0; 1; 0; 2 , 0; 1; 0; 2
|  , 1; 2; 0; 2 , 1; 2; 0; 2
| ||
 , 1; 3; 1; 3 , 1; 3; 1; 3
|  , 6; 9; 4; 8 , 6; 9; 4; 8
| ||
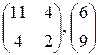 , -3; 1; 0; 7 , -3; 1; 0; 7
|  , -1; 1; 2; 3 , -1; 1; 2; 3
| ||
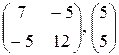 , 0; 1; 0; 1 , 0; 1; 0; 1
|  , 1; 5; 0;1 , 1; 5; 0;1
| ||
 , -2, 11; 20; 30 , -2, 11; 20; 30
| 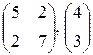 , 1; 3; 2; 3 , 1; 3; 2; 3
| ||
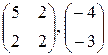 , 1; 3; 0; 2 , 1; 3; 0; 2
| 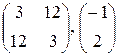 , 1; 3; -3; 1 , 1; 3; -3; 1
| ||
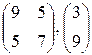 , 0; 1; 0; 1 , 0; 1; 0; 1
| 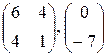 , -2; 0; 2; 4 , -2; 0; 2; 4
| ||
 , 2; 6; 1; 5 , 2; 6; 1; 5
|  , -3; -1; 2; 3 , -3; -1; 2; 3
| ||
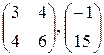 , -20; 0; -10; 20 , -20; 0; -10; 20
| 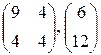 , -5; -2; 0; 2 , -5; -2; 0; 2
|
Контрольные вопросы
1. Дайте определение градиента функции.
2. В какую сторону направлен вектор градиента.
3. Чем отличается метод условного градиента от метода наискорейшего спуска? Для какого класса задач используется метод условного градиента?
4. Дайте определения выпуклого множества.
5. Докажите, что отрезок является выпуклым множеством.
6. Что такое вспомогательное приближение и для чего оно используется?
7. Почему 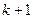 приближение, получаемое по формуле (13), не выходит за пределы выпуклого множества
приближение, получаемое по формуле (13), не выходит за пределы выпуклого множества 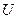
|
|
|


