 |
Задание к лабораторной работе
|
|
|
|
Разработать программу, реализующую метод ломанных для заданной функции  и отрезка
и отрезка 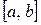 .
.
В программе предусмотреть выполнение итераций до тех пор, пока разность 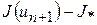 не станет меньшей
не станет меньшей 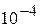 (см. оценку (3)).
(см. оценку (3)).
В результатах должно быть представлено: значение точки глобального минимума 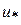 , минимальное значение функции
, минимальное значение функции 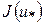 , а также количество итераций.
, а также количество итераций.
Варианты заданий
| № вар. | 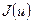
| 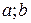
| 
| 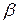
| 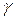
| 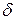
|
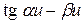
| -0.9; 0.5 | 1.5773 | 2.3041 | |||
| -0.5; 0.7 | 2.2982 | 3.2258 | ||||
| -0.4; 0.2 | 3.7855 | 5.5300 | ||||
| -0.15; 0.09 | 9.1484 | 13.3641 | ||||
| -0.1; 0.2 | 5.9937 | 8.7558 | ||||
| -0.15; 0.1 | 7.8864 | 11.5207 | ||||
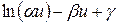
| 0.4; 3.0 | 7.6220 | 8.5900 | 0.5 | ||
| 1.0; 3.0 | 6.0976 | 6.8720 | 1.0 | |||
| 2.0; 7.0 | 4.5732 | 5.1540 | 1.5 | |||
| 3.5; 7.5 | 3.9634 | 4.4868 | 2.0 | |||
| 4.0; 8.0 | 3.0488 | 3.4360 | 2.5 | |||
| 6.0; 9.9 | 1.5244 | 1.7180 | 3.0 | |||

| -0.3; 4.0 | 9.3300 | 6.9770 | 7.25 | ||
| -1.8; 6.2 | 7.6670 | 5.9830 | 6.00 | |||
| -2.1; 6.9 | 6.6700 | 5.3870 | 5.25 | |||
| -3.0; 7.5 | 5.6700 | 4.7940 | 4.50 | |||
| -3.5; 8.1 | 4.3300 | 4.0080 | 3.50 | |||
| -5.0; 9.7 | 2.6700 | 3.0440 | 2.25 | |||

| -2.1; 2.7 | 0.9737 | 0.5067 | |||
| -2.2; 2.3 | 0.9286 | 0.5185 | ||||
| -2.8; 2.2 | 0.5458 | 0.5391 | ||||
| -2.4; 2.4 | 0.7593 | 0.5683 | ||||
| -1.9; 2.1 | 0.5909 | 0.6286 | ||||
| -2.6; 2.0 | 0.4474 | 0.6909 | ||||
| -2.2; 2.4 | 0.1667 | 0.8571 | ||||
| -1.8; 2.3 | 0.7308 | 0.5778 | ||||
| -2.5; 1.9 | 0.8330 | 0.5455 | ||||

| -17; 14 | 0.1697 | -0.5693 | -1.600 | 3.73 | |
| -11; 11 | 1.0390 | -3.1450 | -1.940 | 8.00 | ||
| -3; 8 | 4.6839 | -14.0400 | -2.448 | 23.50 |
Контрольные вопросы
1. Дайте определение липшицевой функции.
2. Геометрическая интерпретация липшицевости функции.
3. Будет ли ломанная линия, получаемая при помощи метода ломанных, пересекать график функции  и почему.
и почему.
4. Из чего следует соотношение (4)? Обосновать ответ.
5. К чему может привести заниженная оценка константы Липшица и почему?
|
|
|
Лабораторная работа №3. Метод касательных
Метод касательных, как и метод ломаных, позволяет найти глобальный минимум функции на отрезке. Метод касательных применим для выпуклых на отрезке функций.
Постановка задачи
Найти точку минимума выпуклой функции  на отрезке
на отрезке 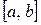 . Вычислить минимальное значение функции.
. Вычислить минимальное значение функции.
Теоретическая часть
Алгоритм
Опр. 1. Функция  называется выпуклой на отрезке
называется выпуклой на отрезке 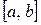 , если для любых
, если для любых 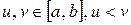 , и для любого
, и для любого 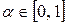 справедливо:
справедливо:
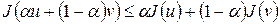 (1)
(1)
Соотношение (1) имеет следующий геометрический смысл. Хорда, соединяющая точки 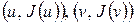 должна быть не ниже значения функции на отрезке
должна быть не ниже значения функции на отрезке  (Рис. 2 -
(Рис. 2 -  ).
).
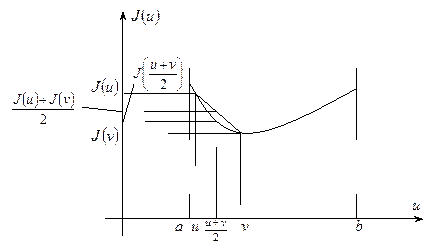
Рис. 2. Геометрический смысл выпуклой функции
Теперь опишем сам метод касательных.
Выберем произвольную точку 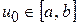 ; например, можно взять:
; например, можно взять:
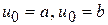 или
или 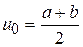 .
.
В данной точке построим касательную к графику функции:
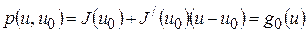 (2).
(2).
После ее построения найдем точку  , удовлетворяющую соотношению:
, удовлетворяющую соотношению:
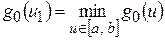 (3)
(3)
Нулевая итерация завершена.
На следующей иитерации построим новую касательную, соответствующую точке  :
: 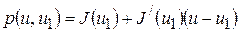 , найдем функцию
, найдем функцию  и затем - следующую точку
и затем - следующую точку 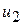 , удовлетворяющую соотношению:
, удовлетворяющую соотношению:  .
.
Рассмотрим k-ю итерацию. К её началу известна точка  и функция
и функция 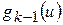 . Строим касательную
. Строим касательную 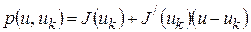 , затем - функцию
, затем - функцию 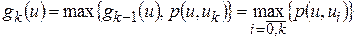 и находим следующую точку
и находим следующую точку  , удовлетворяющую соотношению:
, удовлетворяющую соотношению: 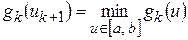 .
.
В итоге мы получаем ломанную линию 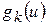 , которая по мере увеличения числа
, которая по мере увеличения числа  приближается к функции
приближается к функции  снизу (Рис. 3).
снизу (Рис. 3).
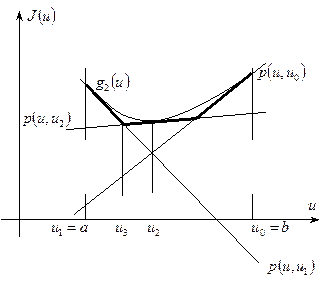
Рис. 3. Ломанная линия приближается снизу по мере увеличения 
Итерации выполняются до тех пор, пока не будет достигнута заданная точность  , см. следующий раздел «Сходимость и оценка погрешности метода».
, см. следующий раздел «Сходимость и оценка погрешности метода».
Сходимость и оценка погрешности метода
Метод касательных сходится, что утверждается в следующей теореме.
Теорема 1. Пусть  на
на 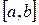 выпукла и дифференцируема, а последовательность
выпукла и дифференцируема, а последовательность 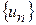 получена описанным выше методом касательных, причем
получена описанным выше методом касательных, причем  ,
, 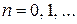 . Тогда:
. Тогда:
1)  и справедлива оценка:
и справедлива оценка:
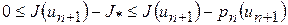 ,
, 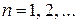 (4)
(4)
2)  .
.
Задание к лабораторной работе
|
|
|
Разработать программу, реализующую алгоритм метода касательных для функции  на отрезке
на отрезке 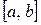 . В качестве начальной точки
. В качестве начальной точки 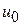 взять
взять 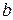 . Итерации выполнять до тех пор, пока разность
. Итерации выполнять до тех пор, пока разность 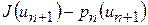 будет больше
будет больше  .
.
В результатах представить: значение точки минимума 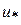 для
для  (см. варианты), минимальное значение функции
(см. варианты), минимальное значение функции 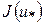 , количество итераций
, количество итераций 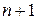 .
.
Варианты заданий
См. варианты заданий к лабораторной работе № 2.
Контрольные вопросы
1. Дайте определение выпуклой функции.
2. Геометрическая интерпретация выпуклой функции.
3. Всякая ли «липшицева» функция является выпуклой, и наоборот, всякая ли выпуклая функция является «липшицевой» и почему?
4. Каким образом определяется точка  после построения ломанной
после построения ломанной 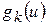 ?
?
Лабораторная работа №4. Градиентные методы
Постановка задачи
Найти при помощи градиентных методов точку минимума дифференцируемой функции многих переменных  .
.
Теоретическая часть
В данной лабораторной работе рассматриваются два метода:
1. метод наискорейшего спуска;
2. метод условного градиента.
Метод наискорейшего спуска
Алгоритм
Метод наискорейшего спуска является одной из разновидностей семейства градиентных методов. В общем виде градиентный метод заключается в построении минимизирующей последовательности 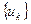 по правилу:
по правилу:
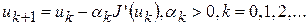 , (1)
, (1)
где 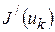 - градиент функции
- градиент функции  в точке
в точке  .
.
Число  из (1) называется шагом. Именно способом выбора
из (1) называется шагом. Именно способом выбора  один градиентный метод отличается от другого.
один градиентный метод отличается от другого.
В случае градиентного метода наискорейшего спуска шаг  определяется из следующего соотношения:
определяется из следующего соотношения:
 , где
, где
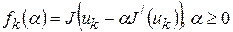
Это означает, что для нахождения значения  на каждом шаге метода наискорейшего спуска приходится решать вспомогательную задачу минимизации функции одной переменной. Такая задача не всегда решается просто. Тем не менее, для некоторых классов функций
на каждом шаге метода наискорейшего спуска приходится решать вспомогательную задачу минимизации функции одной переменной. Такая задача не всегда решается просто. Тем не менее, для некоторых классов функций  значение
значение  удается найти аналитически. В настоящей лабораторной работе рассматривается один из этих классов, а именно:
удается найти аналитически. В настоящей лабораторной работе рассматривается один из этих классов, а именно:
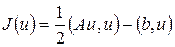 (2)
(2)
Здесь 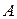 положительно определенная симметричная матрица порядка
положительно определенная симметричная матрица порядка 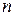 ,
, 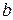 - вектор из
- вектор из 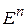 .
.
Градиент функции (1) имеет вид 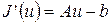 . В силу (1) имеем итерационную формулу градиентного метода:
. В силу (1) имеем итерационную формулу градиентного метода:
 . (3)
. (3)
причем  (3) вычисляется по формуле:
(3) вычисляется по формуле:
 (4)
(4)
В качестве 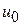 можно выбирать любую точку пространства
можно выбирать любую точку пространства 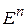 . В качестве критериев окончания счета можно использовать следующие неравенства:
. В качестве критериев окончания счета можно использовать следующие неравенства:
|
|
|
 ;
;
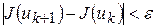 ; (5)
; (5)

|
|
|


