 |
Описание установки и вывод расчетной формулы
|
|
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
| ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» |
Кафедра физики
ЕН.Ф. 03 ФИЗИКА
ЕН.Ф. 03 ФИЗИКА И БИОФИЗИКА
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Уфа 2006
УДК 535
ББК 22.34
Л 12
Рекомендовано к изданию методической комиссией факультета электрификации и автоматизации сельского хозяйства (протокол №2 от «31» октября 2006 г.)
Составитель: доцент Гайсина Г.А.
Рецензент: зав. кафедрой автоматики и электроники, профессор Иванов А.И.
Ответственный за выпуск: заведующий кафедрой физики Юмагужин Р.Ю.
Лабораторный практикум предназначен для студентов всех специальностей.
ОГЛАВЛЕНИЕ
| Введение | ||
| Лабораторная работа №1 Внутреннее трение в жидкостях. Определение коэффициента внутреннего трения жидкостей методом Стокса | ||
| Лабораторная работа №2 Определение коэффициента внутреннего трения газов и длины свободного пробега их молекул | ||
| Лабораторная работа № 3 Определение влажности воздуха | ||
| Лабораторная работа №4 Газовые процессы и определение адиабатической постоянной | ||
| Лабораторная работа №5 Определение изменения энтропии при нагреве и плавлении олова | ||
| Лабораторная работа №6 Явление поверхностного натяжения жидкости. Определение коэффициента поверхностного натяжения жидкости | ||
| Библиографический список | ||
| Приложение А | ||
| Приложение Б | ||
| Приложение В |
|
|
|
Введение
Лабораторный практикум по молекулярной физике и термодинамике имеет своей целью укрепление знаний материала, непосредственное ознакомление студентов с рядом физических явлений и закономерностей и с методикой определения физических параметров.
Молекулярная физика и термодинамика изучают макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический.
Практикум соответствует требованиям Государственного образовательного стандарта высшего профессионального образования и предназначен для студентов всех направлений, изучающих физику.
При подготовке к занятиям студент обязан составить конспект по теоретическому материалу, указанному в лабораторной работе.
Ряд рисунков и обозначений, приведенных в практикуме, может иметь некоторые отличия от схем используемого в работе оборудования, в связи с его модернизацией.
Лабораторный практикум составлен на основе методических указаний, разработанных преподавателями кафедры физики БГАУ Дусыевым В.М., Гайсиной Г.А., Посняком В.К.
Лабораторная работа №1
Внутреннее трение в жидкостях. Определение коэффициента внутреннего трения жидкостей методом Стокса
Цель и задача работы: ознакомление с физической природой вязкости жидкостей и газов, определение вязкости жидкости при комнатной температуре.
Общие сведения
Всем реальным жидкостям и газам присуща вязкость (внутреннее трение). Движение, возникающее в жидкости или газе после прекращения действия сил, вызывающих его, уменьшается из-за сил внутреннего трения.
Явление вязкости в жидкости и газах можно рассматривать следующим образом. Пусть два слоя жидкости или газа, отстоящие друг от друга на расстоянии 
, имеют скорости 
и 
.
|
|
|
Со стороны слоя, который движется быстрее, на слой, движущийся медленнее, действует ускоряющая его сила.
Наоборот, на «быстрый» слой действует тормозящая сила со стороны «медленного» слоя. Это сила внутреннего трения, направленная по касательной к поверхности слоя. Она тем больше, чем больше площадь соприкасающихся слоев, и зависит от изменения скорости течения жидкости (газа) при переходе от слоя к слою (уравнение Ньютона):
, (1)
где 
— динамическая вязкость жидкости (газа), Па×с; 
- градиент скорости - изменение скорости отнесенное к расстоянию между слоями в направлении, перпендикулярном скорости, 
; 
— площадь соприкосновения слоев, м 2.
Если течение жидкостей подчиняется уравнению (1), то вязкость не зависит от градиента скорости, а определяется природой жидкости (газа), температурой и давлением. Вязкость газов при повышении температуры увеличивается, жидкостей - уменьшается. Это указывает на различный механизм их внутреннего трения. Выравнивание скоростей движения соседних слоев газов можно объяснить тем, что из слоя газа, движущегося с большей скоростью, импульс переносится к слою, у которого скорость меньше, и наоборот.
Описание установки и вывод расчетной формулы
В состав лабораторной установки входят: прозрачный цилиндрический сосуд с исследуемый жидкостью, набор металлических шариков, микрометр, секундомер.
Согласно закону Стокса, при движении шарика в вязкой жидкости с небольшой скоростью, когда нет вихрей, сила сопротивления равна
, (2)
где 
— вязкость жидкости; 
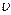— скорость движения шарика, м/с; 
— радиус шарика, м.
На движущийся шарик с плотностью ρ и объемом V в жидкости действуют три силы (рисунок 1): сила сопротивления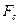 
, сила тяжести 
и выталкивающая (архимедова) сила 
.
Рисунок 1 Движение шарика в жидкости
Учитывая, что масса 
, объем шарика 
, получаем силу тяжести:
(3)
и выталкивающую силу:
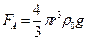, (4)
где 
— плотность жидкости, кг/м 3. Сила тяжести и выталкивающая сила постоянны, сила сопротивления прямо пропорциональна скорости. После опускания шарика в жидкость он движется ускоренно. По мере увеличения скорости увеличивается и сила сопротивления и при определенной скорости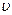 
наступает момент, когда сумма всех действующих сил на шарик равна нулю, и он начинает двигаться равномерно.
|
|
|
В этом случае имеем равенство
. (5)
Подставляя значения сил из формул (2-4) в (5), получаем
.
Откуда
. (6)
Для определения вязкости по методу Стокса используется прозрачный цилиндрический сосуд с исследуемой жидкостью (рисунок 2). На нем имеются две кольцевые метки А и В. Метка А соответствует той высоте, начиная с которой движение шарика становится заведомо равномерным. Нижняя метка В нанесена для удобства отсчета времени.
Опуская шарик в сосуд, отмечают по секундомеру время 
прохождения шариком расстояния 
между метками АВ. Так как 
, то формула (6) принимает вид:
, (7)
где 
- диаметр шарика, м.
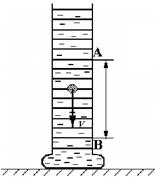
Рисунок 2 Цилиндрический сосуд с исследуемой жидкостью
Введя обозначение С = 
, получим расчетную формулу
. (8)
|
|
|
