 |
Порядок выполнения работы и требования
|
|
|
|
К оформлению результатов
3.1 При подготовке к лабораторной работе необходимо изучить и законспектировать следующие библиографические источники:
- для неинженерных специальностей С. 153–158, 164–166 /1/.
- для инженерных специальностей С. 175–184, 191–194 /2/; С. 95–97 /3/.
3.2 Ознакомиться с установкой и методикой выполнения работы.
3.3 Измерить микрометром диаметр шарика.
3.4 Измерить время прохождения 
шариком расстояния между метками А и В.
3.5 Измерить расстояние 
между метками.
3.6 Вычислить вязкость 
по формуле (7) или (8).
3.7 Произвести аналогичные измерения и вычисления еще минимум с четырьмя шариками и найти 
по формуле
,
где 
- количество измерений.
3.8 Определить абсолютную погрешность для каждого опыта по формуле
- - - - - - - -
.
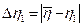
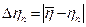3.9 Вычислить среднеквадратичное отклонение коэффициента вязкости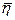 
.
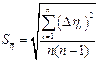3.10 По таблицам коэффициентов Стъюдента (приложение А) найти 
для n и доверительной вероятности Р =0,997.
3.11 Вычислить погрешность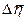 
по формуле
.
3.12 Определить относительную погрешность по формуле
.
3.13 Результаты измерений и расчетов представить в таблице 1.
Таблица 1 Параметры установки, результаты измерений и вычислений
| №, п/п | Обозначения физических величин | |||||||||
| 
|  , м
|  , м
|  , с
|
| 
| 
| 
| 
| |
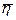
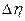
3.14 Записать окончательный результат в виде
.
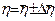3.15 Сделать выводы.
4 Контрольные вопросы
4.1 От чего зависит сила внутреннего трения?
4.2 Чем обусловлено внутреннее трение в жидкостях?
4.3 Какие силы действуют на шарик, движущийся в жидкости?
4.4 В каких единицах измеряется коэффициент вязкости?
|
|
|
4.5 Что называется градиентом скорости?
4.6 Какое течение называется ламинарным, а какое турбулентным?
4.7 Что характеризует число Рейнольдса?
4.8 Какими параметрами и как определяется вязкость жидкости?
4.9 Какой характер течения жидкости рассматривается в методе Стокса по определению вязкости? Почему?
4.10 Охарактеризовать зависимость вязкости жидкости от температуры.
4.11 Как связана вязкость с гидродинамической теорией смазки?
Лабораторная работа №2
Определение коэффициента внутреннего трения газов и длины свободного пробега их молекул
Цель и задача работы: ознакомление с природой внутреннего трения в газах, освоение одного из методов определения длины свободного пробега молекулы и коэффициента вязкости воздуха.
Общие сведения
Расстояние, которое пролетает молекула между двумя последовательными столкновениями, называют длиной свободного пробега и обозначают 
. Длины свободного пробега между отдельными столкновениями молекулы могут значительно отличаться друг от друга. Поэтому пользуются средней длиной свободного пробега 
:
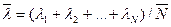, (1)
где 
- число соударений.
Если обозначает среднее число соударений молекулы газа за одну секунду, то сумма в числителе формулы (1) будет выражать путь, пройденной молекулой за 1 с, т.е. среднюю скорость движения молекулы 
. Таким образом,
= 
. (2)
Физические процессы, происходящие в потоке жидкости или газа, а также при движении твердого тела в жидкости или газе, существенно зависят от вязкости этих веществ.
Внутреннее трение возникает между двумя соседними слоями газа при их относительном движении. Очевидно, молекулы газа при своем движении совершают не только упорядоченное, но и беспорядочное тепловое движение, переходя из одного слоя в другой и обратно. Каждая молекула, имеющая массу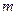 
при переходе из одного слоя в другой, изменяет свой импульс на 
. В этом случае возникает сила трения, действующая на данный слой со стороны соседних слоев. Эта сила пропорциональна площадке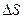 
, лежащей в плоскости соприкосновения двух слоев газа, градиенту скорости 
и действует по касательной к поверхности раздела слоев.
|
|
|
Закон внутреннего трения был установлен И. Ньютоном и имеет вид
, (3)
где 
- коэффициент внутреннего трения (динамическая вязкость), Па×с.
Динамическая вязкость численно равна силе, действующей на единицу площади при градиенте скорости, равном единице.
В системе СГС динамическая вязкость измеряется в Пуазах (П).
1 Па × с = 10 П.
|
|
|
