 |
Классификация ЛПП систем по форме импульсной характеристики
|
|
|
|
Одномерные последовательности. Их классификация и способы задания
Два способа записи последовательности:
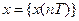– отражает процесс дискретизации непрерывного во времени сигнала, где 
.
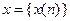короче и используется в случае, когда не требуется учитывать реальный масштаб времени.
Интервал определения последовательности может быть
- Конечным:
, где 
, 
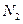– целые. Имееп последовательность конечной длины - Полубесконечным:
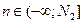– левосторонняя или 
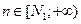– правосторонняя - Бесконечным:
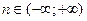– двусторонняя.
Для унификации всякую последовательность обычно приводят к бесконечной, полагая отсчеты, лежащие вне интервала определения, тождественно равными нулю.
Последовательность называется детерминированной, если можно точно указать ее значение для любого момента дискретного времени 
.
Последовательность – случайная, если ее элементы – случайные величины.
Способы задания детерминированной последовательности:
1) Задание значений: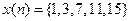 
2) Аналитическое задание: 
3) Аналитически через дискретизированную функцию: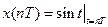 
4) Через рекуррентную функцию: 
, 
5) Графический способ: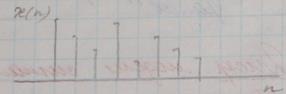 
Примеры последовательностей:
1) Единичный импульс: 
2) Единичный скачок: 
3) Дискретная правосторонняя экспонента: 
4) Дискретная комплексная экспонента: 
, где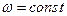 
, имеющая смысл безразмерной частоты
Дискретные ЛИС-системы. Импульсная характеристика.
Опр. Дискретной системой будем называть некоторое правило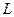 
, по которому входная последовательность 
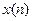преобразовывается в выходную последовательность 
: 
.
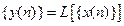Опр. Дискретная система 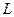называется линейной, если для нее соблюдается принцип суперпозиции: 
.
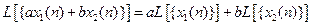Опр. Дискретная система 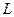называется системой с постоянными параметрами, если 
выполняется 
, то есть если она обладает свойством инвариантности ко времени.
|
|
|
Опр. Дискретные системы, обладающие одновременно свойствами линейности и инвариантности к сдвигу, называются дискретными линейными системами с постоянными параметрами (ЛПП-системами).
Чтобы описать систему с информационной точки зрения, нужно указать конкретное правило преобразования входного сигнала в выходной. ЛПП-систему можно описать с помощью ее импульсной характеристики.
Опр. Импульсная характеристика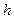 
дискретной ЛПП-системы определяется как реакция системы на входное воздействие в форме единичного импульса: 
.
Полная выходная последовательность записывается в виде свертки: 
.
Свойства свертки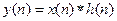 
:
1) Коммутативность: 
;
2) Ассоциативность: 
3) Дистрибутивность: 
4) Фильтрующее свойство единичного импульса: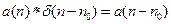 
5) Свободное суммирование сдвига. Если 
, 
6) Для ЛПП-системы при последовательном соединении звеньев с ИХ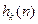 
: 
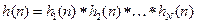
7) Для ЛПП-системы при параллельном соединении звеньев с ИХ :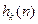 
.
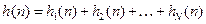Физическая реализуемость ЛИС-систем.
Опр. Дискретная система называется физически реализуемой, если значение выходной последовательности в произвольный момент 
зависит только от значений входной последовательности при 
.
Для физически реализуемой системы отклик не опережает входное воздействие.
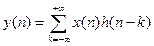. Для физической реализуемости должно быть 
при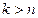 
, 
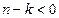. Отсюда необходимое и достаточное условие физической реализуемости ЛПП-системы: 
при 
.
Устойчивость ЛИС-систем
Опр. Дискретная система называется устойчивой, если любому ограниченному входному воздействию соответствует ограниченный отклик, то есть если для любых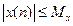 
выполняется 
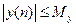, где 
.
Теорема. Необходимым и достаточным условием устойчивости ЛПП-системы является абсолютная суммируемость импульсной характеристики:
(*)
Доказательство:
- Необходимость. Рассмотрим ограниченную входную последовательность:
.
|
|
|
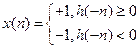Найдем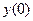 
:
. Пусть (*) не выполняется, но тогда система 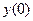не существует, а значит, система не является устойчивой по определению. Получили противоречие, следовательно, (*) является необходимым условием устойчивости.
- Достаточность. Пусть (*) выполняется и 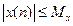. Тогда, используя свойство коммутативности свертки, получим:
, то есть выходная последовательность ограничена и исходная система устойчива.
Классификация ЛПП систем по форме импульсной характеристики
КИХ-системы. У ЛПП-систем с конечной импульсной характеристикой (КИХ-систем), как следует из самого названия, импульсная характеристика представляет собой последовательность конечной длины, т. е. при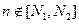 
. КИХ- системы всегда устойчивы, так как для них сумма модулей значений ИХ конечна. При 
такие системы являются физически реализуемыми.
ЛПП-системы с бесконечной импульсной характеристикой (БИХ-системы) имеют в качестве импульсной характеристики
- правостороннюю ( при
), 
- левостороннюю ( при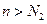
), 
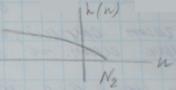
- или двустороннюю (
при 
),
последовательность.
Такие системы могут быть неустойчивыми. Требование физической реализуемости здесь выполнено только в первом случае при .
Если у КИХ- или БИХ-системы импульсная характеристика равна нулю при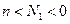 
, то такая система тоже может быть реализована, если допустить задержку в получении сигнала на выходе. Величина этой задержки должна быть достаточной, чтобы «сдвинуть» импульсную характеристику в область неотрицательных значений аргумента, т. е. не меньше 
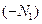. Строго юворя, при этом реализуется не исходная система, а другая, эквивалентная последовательному соединению системы и устройства задержки. Однако в большинстве практических приложений такая замена вполне допустима.
|
|
|
