 |
Факторизация энергетического спектра
|
|
|
|
Синтезировать физически реализуемую устойчивую ЛИС-систему, которая дает на выходе сигнал с заданной АКФ, в то время как на входе будет белый шум.
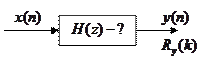
 ,
,  , откуда
, откуда  ,
,  ,
,  .
.
Решение сводится к тому, чтобы разложить 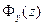 на такие множители. Процедуру разложения энергетического спектра на такие множители и называют факторизацией.
на такие множители. Процедуру разложения энергетического спектра на такие множители и называют факторизацией.
Требования:
1.  должна соответствовать физически реализуемой системе, то есть должна быть дробно-рациональной функцией по отрицательным степеням
должна соответствовать физически реализуемой системе, то есть должна быть дробно-рациональной функцией по отрицательным степеням 
2.  должна соответствовать устойчивой системе, то есть иметь полюса, лежащие внутри единичной окружности.
должна соответствовать устойчивой системе, то есть иметь полюса, лежащие внутри единичной окружности.
Известно, что если 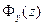 действительно спектр мощности, то
действительно спектр мощности, то  ,
,  , то подобное разложение (возможно) существует всегда.
, то подобное разложение (возможно) существует всегда.
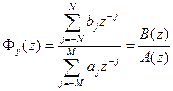 , где
, где  и
и  . Рассмотрим многочлен в знаменателе.
. Рассмотрим многочлен в знаменателе.  . Найдем полюсы
. Найдем полюсы  , – всего
, – всего 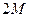 корней. Если
корней. Если  – корень уравнения, то
– корень уравнения, то  – тоже корень. Если
– тоже корень. Если  , то
, то  , следовательно, на единичной окружности корней нет.
, следовательно, на единичной окружности корней нет.  ,
,  – те, которые лежат внутри единичной окружности.
– те, которые лежат внутри единичной окружности.  . Введем обозначение
. Введем обозначение  и отнесем в его первое произведение и домножим на
и отнесем в его первое произведение и домножим на  .
.


 , откуда
, откуда  .
.
Аналогично с  :
:  , где
, где  ,
,  – корни
– корни  .
.
Уравнение  имеет право иметь корни на единичной окружности и не требует, чтобы
имеет право иметь корни на единичной окружности и не требует, чтобы 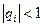 . Но условие:
. Но условие:  ,
,  – не должно быть парных корней (типа
– не должно быть парных корней (типа  и
и  ).
).
Пример:
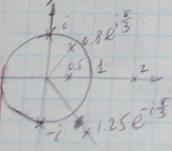
 – нормально,
– нормально,  – нормально,
– нормально,  – нельзя.
– нельзя.
 , где
, где  – дробно-рациональная функция от
– дробно-рациональная функция от  , все полюсы которой лежат внутри единичной окружности.
, все полюсы которой лежат внутри единичной окружности.
Можем взять  ,
,  потому что характеристика Спроц. Не зависит от сдвига.
потому что характеристика Спроц. Не зависит от сдвига.
Если на входе  , а на выходе АКФ
, а на выходе АКФ  ,
,  ,
, 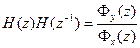 ,
,  ,
,  ,
,  теперь важно, чтобы корни
теперь важно, чтобы корни  удовлетворяли требованиям, предъявляемые
удовлетворяли требованиям, предъявляемые 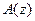 .
.
Если уравнение  имеет корни, лежащие на единичной окружности и они не компенсируются корнями уравнения
имеет корни, лежащие на единичной окружности и они не компенсируются корнями уравнения  , то система получится неустойчивой.
, то система получится неустойчивой.
Постановка задачи восстановления сигналов. Оптимальное и квазиоптимальное восстановление
|
|
|
Пусть имеется некоторый полезный сигнал  , однако непосредственному наблюдателю он недоступен. В нашем распределении есть сигнал
, однако непосредственному наблюдателю он недоступен. В нашем распределении есть сигнал  .
.

Наша задача – оценить сигнал  по имеющемуся
по имеющемуся  .
.

Уточнения:
1. Будем считать искажающую систему устойчивой ЛИС-системой с известной импульсной характеристикой  . Тогда
. Тогда  – линейная модель наблюдений в дискретный момент времени.
– линейная модель наблюдений в дискретный момент времени.
2. Восстанавливающая ЛИС-система с ИХ 

3. 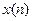 ,
,  – стационарная случайная последовательность (ССП) и известны их статистические характеристики
– стационарная случайная последовательность (ССП) и известны их статистические характеристики
4. Ошибка восстановления  – случайная последовательность. Будем строить такую восстанавливающую систему, которая минимизирует среднеквадратическую ошибку:
– случайная последовательность. Будем строить такую восстанавливающую систему, которая минимизирует среднеквадратическую ошибку: 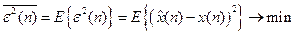
Наша цель – найти ИХ восстанавливающей ЛИС-системы, которая обеспечит минимизацию среднеквадратической ошибки. Такая ЛИС-система будет называться оптимальной линейной восстанавливающей системой или оптимальным линейным восстанавливающим фильтром.
Часто на  налагают какие-нибудь ограничения и мы получаем квазиоптимальную процедуру восстановления.
налагают какие-нибудь ограничения и мы получаем квазиоптимальную процедуру восстановления.
Есть интервал  , на котором ищем
, на котором ищем  и
и  при
при  .
.
 . Тогда среднеквадратичная ошибка будет равна:
. Тогда среднеквадратичная ошибка будет равна:
 ,
,  ,
,  ,
,  .
.  ,
,  штук.
штук. 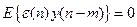 ,
,  .
.
То есть ошибка оптимального восстановления не коррелируется с выходным сигналом – лемма об ортогональном проецировании  ,
,  – уравнение Винера-Хопфа.
– уравнение Винера-Хопфа.
Для определения импульсной характеристики оптимального (или квазиоптимального) фильтра получим систему:
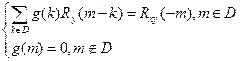
Определим ошибку восстановления по полученному  .
. 
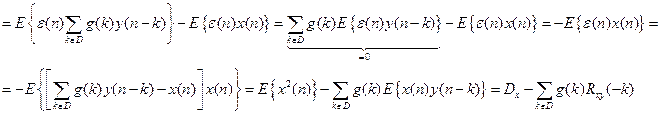
Окончательно,  .
.
Рассмотрим частный случай, белый шум и отсутствие [недописано]
 ,
,  .
.
Известно, что 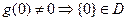 ,
,
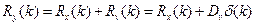 ,
,
 .
.
Из уравнения Винера-Хопфа
 ,
, 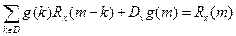 .
.
Тогда при 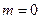
 ,
, 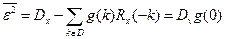
Уравнение Винера-Хопфа. Лемма об ортогональном проецировании
[Необходимо дополнить]
|
|
|


