 |
Задача проектирования цифровых фильтров, этапы ее решения
|
|
|
|
Опр. Цифровым фильтром принято называть ЛИС-систему, реализованную при помощи некоторого арифметического устройства. Цифровые фильтры используются как и аналоговые фильтры.




Нужно учитывать характеристики сигнала, поэтому  .
.
Задача проектирования цифрового фильтра заключается в построении дискретной ЛИС-системы с заданныой частотной характеристикой. Эта задача решается в несколько этапов.
- Определение требуемых свойств фильтра: задается ЧХ, анализируется спектр входного сигнала, определяется идеальная ЧХ.
 и шаг дискретизации в безразмерных частотах.
и шаг дискретизации в безразмерных частотах.
В большинстве случаев  – полосовый фильтр.
– полосовый фильтр.
Физически выполнить эти требования невозможно. Обычно задаются допуски на отклонение ЧХ от идеальной. 
Иногда налагаются дополнительные требования на фазу ЧХ: 
- Аппроксимация ЧХ
- Выбор структуры информационного фильтра. Выбирается схема ЛИС-системы
- Анализ погнешности квантования. Погрешность возникает в из-за округления коэффициентов фильтра и округления промежуточных результатов.
- Имитация цифрового фильтра (моделирование). Экспериментально проверяют, удовлетворяет ли заданный фильтр требованиям.
Различают нерекурсивный и рекурсивный цифровые фильтры.
Опр. Нерекурсивный цифровой фильтр – такой, в котором отсчет выходной последовательности равен взвешенной сумме отсчетов входной последовательности:
 – физически не реализуемый нерекурсивный фильтр
– физически не реализуемый нерекурсивный фильтр
 – физически реализуемый нерекурсивный фильтр, КИХ-система
– физически реализуемый нерекурсивный фильтр, КИХ-система
Опр. Рекурсивный цифровой фильтр – отсчеты выходной последовательности формируются с учетом предыдущих отсчетов этой выходной последовательности:
 – БИХ-фильтр (в общем случае случайный)
– БИХ-фильтр (в общем случае случайный)
|
|
|
Задача проектирования КИХ-фильтров
Пусть  ,
,  .
.  .
. 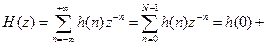
 .
.
Зная передаточную функцию, можно выписать ЧХ:  .
.
Задача проектирования КИХ-фильтра сводится к задаче аппроксимации функции  полиномом степени
полиномом степени 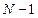 . Находим коэффициенты полинома (они же импульсная характеристика). Если возникает дополнительное требование линейности фазы ЧХ
. Находим коэффициенты полинома (они же импульсная характеристика). Если возникает дополнительное требование линейности фазы ЧХ 
 .
.  ,
,  .
. 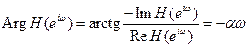 ,
,  ,
,  . Решим это как уравнение относительно
. Решим это как уравнение относительно  .
.
а)  ,
,  ,
,  ,
, 
б) 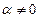 ,
,  .
.  ,
, 
 .
.  , тогда для фильтра с линейной фазой ИХ симметрична
, тогда для фильтра с линейной фазой ИХ симметрична
При 

При 
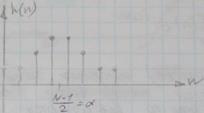
Усечение ИХ идеального фильтра
Пусть  задано.
задано.  , т.е. фаза нулевая. Определим по идеальной ЧХ ее ИХ.
, т.е. фаза нулевая. Определим по идеальной ЧХ ее ИХ.  ,
,  .
.  окажется симметричной, следовательно, четной.
окажется симметричной, следовательно, четной. 
Данная 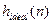 нам не годится. Нужно ее ограничить или усечь.
нам не годится. Нужно ее ограничить или усечь.
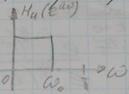


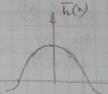
Величина колеблется до 10% от значения в полосе пропускания.


Становятся чаще колебания, если возьмем шире спектр.
 ,
,  – прямоугольное окно.
– прямоугольное окно.  ей соответствует
ей соответствует 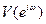 ,
,  соответствует
соответствует  , а
, а  –
– 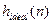 . Рассчитаем
. Рассчитаем 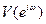 :
: 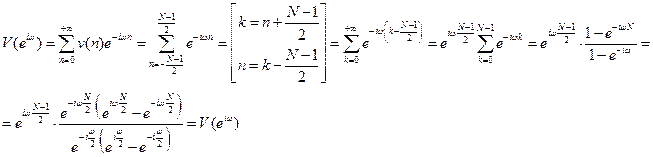

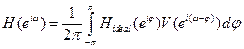
Метод взвешивания
Метод взвешивания заключается в том, чтобы выбирать так, что спектр был бы гладким. Идеальная ИХ умножается на функцию некоторого окна:  . Наложим некоторые ограничения на
. Наложим некоторые ограничения на  :
:
1. Она должна быть ограничена: 

2. Спектр функции окна должен иметь по возможности малые колебания, боковые лепестки.

3. Спектр функции окна должен быть как можно более узким.



Требования эти, как правило, противоречивы.
Примеры функции окна:
1) Прямоугольная:  .
.  . Боковые лепестки большие, из-за них возникает эффект Гиббса.
. Боковые лепестки большие, из-за них возникает эффект Гиббса.
2) Обобщенное окно Хэмминга:  ,
,  . Обычно берется
. Обычно берется 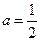 .
. 
 . Практически отсутствуют боковые лепестки.
. Практически отсутствуют боковые лепестки.
Достаточность метода взвешивания:
1) Универсальность
2) Относительная простота
Недостатки
1) Трудно получить хорошее качество аппроксимации
2) Недостаточная гибкость при проектировании
Метод частотной выборки
1) КИХ-фильтр описывается значениями своей ИХ в конечном числе своих точек. Например,  ,
,  . Также однозначно задает его и ДПФ ЧХ
. Также однозначно задает его и ДПФ ЧХ  ,
,  .
.
2) Однозначная связь ДПФ с непрерывным спектром последовательности конечной длины:  . Получается дискретизацией ЧХ.
. Получается дискретизацией ЧХ.
|
|
|
3) Можно осуществить обратный переход.  и
и 
Пусть задан  . Произведем дискретизацию от
. Произведем дискретизацию от  до
до  .
.  . Этого достаточно, чтобы построить КИХ-фильтр. В выбранных точках погрешность аппроксимации равна нулю, она будет возникать только в промежуточных.
. Этого достаточно, чтобы построить КИХ-фильтр. В выбранных точках погрешность аппроксимации равна нулю, она будет возникать только в промежуточных.  ,
,  .
.



|
|
|


