 |
Дискретное преобразование Фурье.
|
|
|
|
Основой цифрового спектрального анализа сигнала является дискретное преобразование Фурье (ДПФ). Оно переводит из временной области в частотную. Ценность – разработаы быстрые алгоритмы.
Пусть  – непрерывная периодическая функция времени с периодом
– непрерывная периодическая функция времени с периодом 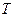 :
:  ,
,  .
.
Ее можно разложить в ряд Фурье или представить через спектр, ряд которого содержит гармонические составляющие с периодами 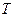 ,
,  ,
, 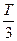 и т.д.:
и т.д.: 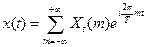 .
.
Опр.  называется базисом преобразования или спектральными компонентами преобразования.
называется базисом преобразования или спектральными компонентами преобразования.
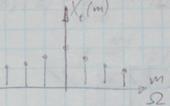
При дискретизировании мы получаем тоже периодическую функцию:  с разложением
с разложением  . Теперь оставим лишь
. Теперь оставим лишь  базисных функций
базисных функций  . Тогда получим дискретный спектр следующего вида:
. Тогда получим дискретный спектр следующего вида:  .
.
Опр. Преобразование  называется дискретным преобразованием Фурье.
называется дискретным преобразованием Фурье.
Теперь домножим обе части этого уравнения на  и просуммируем по
и просуммируем по  от
от 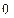 до
до 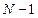 :
:
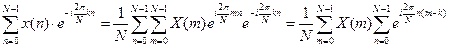 . При
. При 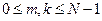
 . Откуда
. Откуда  .
.
Опр.  называется прямым ДПФ.
называется прямым ДПФ.
Опр.  называется обратным ДПФ.
называется обратным ДПФ.
Необходимо помнить, что последовательности 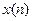 и
и  являются периодическими с периодом
являются периодическими с периодом  :
:

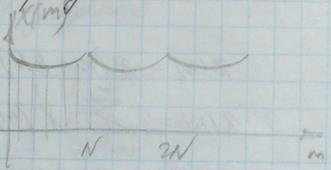
Поскольку при вычислении ДПФ и ОДПФ используются значения только одного периода, то можно все вышесказанное применить и к последовательности, определенной на  , которую, однако, надо продолжать периодически.
, которую, однако, надо продолжать периодически.
Связь ДПФ с непрерывным спектром и Z-преобразованием
Пусть  – последовательность конечной длины,
– последовательность конечной длины, 
 . Вычислим ее
. Вычислим ее  -преобразование:
-преобразование:
 . Вспомним, чему равно ее ДПФ:
. Вспомним, чему равно ее ДПФ:  . Видно, что ДПФ совпадает с
. Видно, что ДПФ совпадает с  -преобразованием, взятым в точке
-преобразованием, взятым в точке  .
. 
По ДПФ можно определить  -преобразование:
-преобразование: 
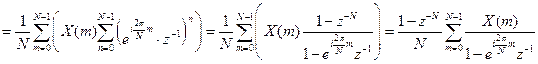 .
.
Как известно, спектр последовательности есть ее  -преобразование при
-преобразование при  :
:  ,
, 
То есть коэффициенты ДПФ – это отсчеты непрерывного спектра, равномерно взятые на интервале  :
:
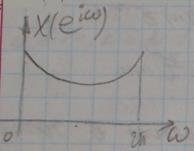
Для обратного перехода от ДПФ к спектру достаточно подставить в формулу для перехода от ДПФ к  -преобразованию
-преобразованию 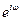 вместо
вместо  .
.
|
|
|
Использование ДПФ для вычисления отсчетов непрерывного спектра
Пусть  – последовательность конечной длины,
– последовательность конечной длины, 
 . Нужно определить
. Нужно определить  отсчетов ее непрерывного спектра
отсчетов ее непрерывного спектра  , равномерно распределенных на интервале
, равномерно распределенных на интервале  .
.
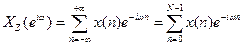 .
.  ,
, 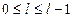 –
–  точек.
точек. 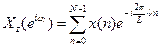 . Рассмотрим
. Рассмотрим  . Определим
. Определим  -точечное ДПФ новой последовательности:
-точечное ДПФ новой последовательности:
 .
.  .
.
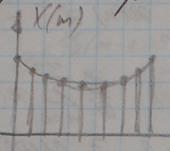
Таким образом, дополнение последовательности конечной длины нулями позволяет получить сколь угодно большое число отсчетов ее непрерывного спектра при помощи ДПФ.
Проиллюстрируем сказанное:

Использование ДПФ для вычисления последовательности по ее спектру
Процедура перехода от непрерывных сигнала к его отсчетам называется дискретизацией. Она влияет на форму полученной последовательности.
Пусть 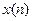 – произвольная последовательность.
– произвольная последовательность.  . Пусть
. Пусть  -преобразование сходится на единичной окружности
-преобразование сходится на единичной окружности  :
:  .
.
Хотим перейти от спектра к исходной последовательности. Вспомним дискретизацию спектра, выберем  равномерно расположенных отсчетов
равномерно расположенных отсчетов  , где
, где  .
.
 (*)
(*)
Рассмотрим сумму  . Тогда (*) будет равно
. Тогда (*) будет равно  .
.
Периодическая последовательность, полученная при помощи ОДПФ из дискретизированного спектра непериодической последовательности состоит из бесконечной суммы сдвинутых копий исходной непериодической последовательности.
Если последовательность конечна и ее длина превышает  , то возникает эффект наложения.
, то возникает эффект наложения.

Основные свойства ДПФ
Свойство 1. Линейность
 ,
, 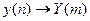 ,
, 
Свойство 2. Периодичность
 ,
, 
Свойство 3. Свойство сдвига
Если 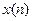 – периодическая с периодом
– периодическая с периодом  и ее ДПФ
и ее ДПФ  , то ДПФ последовательности
, то ДПФ последовательности  имеет вид
имеет вид 


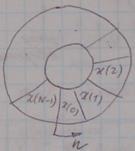
Свойство 4. Циклическая свертка последовательностей
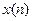 и
и  – периодические с периодом
– периодические с периодом  . Им соответствует ДПФ
. Им соответствует ДПФ  и
и  . Найдем
. Найдем  и вычислим ОДПФ от
и вычислим ОДПФ от  .
.
 – круговая или циклическая свертка,
– круговая или циклическая свертка,  .
. 
Это нелинейная (апериодическая) свертка  .
. 
|
|
|


