 |
Изучение резонансных явлений в электрическом колебательном контуре
|
|
|
|
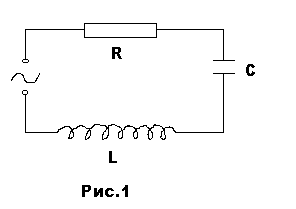
| Одна из разновидностей электрического колебательного контура представляет собой последовательно соединенные конденсатор С, катушку индуктивности L и сопротивление R (рис.1)
Собственная круговая частота колебаний w0 такого контура равна:
 (1)
|
Соответственно, собственная частота колебаний в Герцах для него определяется формулой:
(2)
При включении в контур внешнего источника с периодически изменяющейся ЭДС:
(Е 0 – амплитуда, w - круговая частота колебаний), в нем возникают вынужденные колебания тока с той же частотой w и фазой, отличающейся от фазы ЭДС на величину a:
Амплитуда I 0 вынужденных колебаний тока связана с параметрами контура R, C, L и величиной w соотношением:
Амплитуда I 0 зависит от круговой частоты wприложенной ЭДС. При некоторой частоте wрсила тока максимальна и равна I 0 m = E 0 / R.
Явление резкого увеличения амплитуды колебаний ( здесь - тока I 0 ) при приближении частоты внешнего воздействия w к собственной частоте w 0 колебаний системы называется резонансом.
| Резонансная частота wр совпадает с собственной круговой частотой w0.только при отсутствии потерь энергии в контуре. При наличии потерь wр < w0. Поскольку w = 2p f, где f – частота колебаний в Герцах, зависимость I ( w ) можно заменить зависимостью I(f) (рис.2). |
|
При резонансе напряжение на катушке индуктивности UL и напряжение на конденсаторе Uc максимальны, равны друг другу и противоположны по фазе. Резонанс в электрической цепи с соединёнными последовательно R, C, L называется резонансом напряжений.
Качество любой колебательной системы характеризуется её добротностью Q.
|
|
|
Для колебательного контура добротность характеризует относительные потери электромагнитной энергии в нём за счет омического сопротивления R. Добротность контура определяется уравнением:
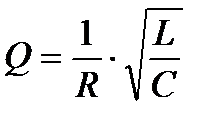
(3)
Величина 
имеет размерность сопротивления и называется волновым сопротивлением контура. Оно характеризует сопротивление, которое оказывает контур распространению в нем синусоидальных колебаний.
Добротность Q определяет ширину резонансной кривой. Острота кривой характеризуется ее относительной полушириной D f = f 2 - f 1 – разностью значений частот f 2 и f 1, соответствующих величине I = I 0 / √2 (рис.2).
Относительная полуширина D f / fp связана с добротностью Q соотношением:
(4)
| ОПИСАНИЕ УСТАНОВКИ (РИС.3) |
|
Синусоидальное напряжение частоты f от звукового генератора ЗГ
подается на колебательный контур, содержащий последовательно соединенные сопротивление R, конденсатор С и катушку индуктивности L. С катушкой L индуктивно связана небольшая катушка L 1, которая соединена с вольтметром переменного тока В. В катушке L 1 индуцируется ЭДС U, пропорциональная величине тока I 0 в контуре. Меняя частоту f подаваемой от ЗГ ЭДС, можно изучать частотную зависимость I 0 в условных единицах напряжения на вольтметре.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для используемого контуразначения L, C и R задаются в лаборатории.
1.Зная параметры контура, вычислить собственную частоту f 0
колебаний по формуле (2) и добротность Q по формуле (3). Результаты расчета занести в таблицу 1.
2.Включить звуковой генератор и вольтметр в сеть и, вращая ручку выходного напряжения, установить предел измерения вольтметра (в делениях верхней шкалы прибора) в соответствии с указаниями преподавателя.
4.Изменяя частоту звукового генератора в пределах частот,указанных в лаборатории,определять для каждой частоты значения выходного напряжения (в делениях верхней шкалы вольтметра) с точностью до 0,5 деления шкалы. Данные занести в таблицу 2.
|
|
|
5.Используя результаты таблицы 2, на миллиметровой бумаге построить график зависимости I от f.
6.С помощью этого графика найти величины резонансной частоты колебаний fp, значение D f = f 2 - f 1 на высоте резонансной кривой равной I м /√2 и вычислить добротность контура Q по формуле (4). Данные занести в таблицу 3.
7.Сравнить теоретические значения собственной частоты f 0 контура и его добротности Q с экспериментально полученными данными для резонансной частоты fp и добротности Q.
ТАБЛИЦА 1
| L,мкГн | C,нФ | R, Ом | f0 кГц | Q |
| f, кГц | и т.д. | |||
| U,дел.шк. |
ТАБЛИЦА 2
ТАБЛИЦА 3
| f p, кГц | I м дел.шк | 
| f 1, кГц | f 2, кГц | D f, кГц | Q |
ЛАБОРАТОРНАЯ РАБОТА № 48
|
|
|
