 |
Принцип оптимальности. Постановка задач оптимального управления динамическими объектами. Примеры задач.
|
|
|
|
Понятие идентификации. Задачи и этапы идентификации. Общая постановка задач идентификации.
Идентификация – это определение структуры и параметров модели (процесса, объекта и системы), обеспечивающих наилучшее совпадение выходных координат моделей и выходных координат реального процесса.
Без решения проблемы идентификации невозможно качественно разработать тех. процесс, спроектировать технологическое оборудование и построить систему управления.
Задача идентификации: по результатам наблюдений за входными и выходными переменными объекта построить оптимальную в некотором смысле его модель, при этом объект находится в нормальном режиме функционирования, т.е. в обстановке случайных возмущения и помех.
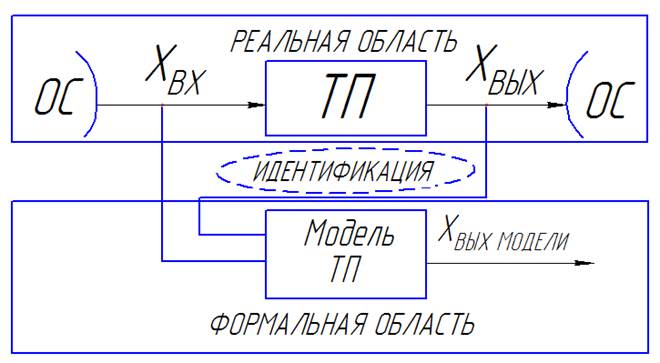
ОС - окружающая среда
ТП – тех. процесс
Задача идентификации решается как на этапе проектирования ТП и системы управления, так и в процессе эксплуатации. Во 2-ом случае (на этапе эксплуатации) идентификация и сама система называются адаптивными. Для достижения цели управления система формирует управляющие сигналы либо корректирует базовые сигналы, приспосабливаясь к изменениям текущих условий.
Принцип оптимальности. Постановка задач оптимального управления динамическими объектами. Примеры задач.
Оптимизация динамических объектов.
Методы динамического программирования:
~ дискретный метод
~ непрерывный динамический метод

Необходимо выбрать наиболее дешевый путь из А в B. Решение следует начинать с конца.
Принцип оптимальности:
Каким бы образом мы не попали в заданную точку, последующее движение должно быть оптимальным.
С точки зрения теории управления:
Оптимальная стратегия (или поведение) объекта обладает тем свойством, что каковы бы не были решения и состояния объекта на начальном этапе, решения на последующем этапе должны составлять оптимальную стратегию относительно состояния, которое было получено в результате принятия решений на начальном этапе.
|
|
|
P.S. также читай вопрос №15.
2. Идентификация как метод построения математических моделей. Классификация математических моделей и методов идентификации.
Одним из главных элементов, необходимых для эффективного решения сложной задачи, является построение и соответствующее исполнение моделей.
МОДЕЛЬ – это представление объекта или системы в некоторой форме, отличной от формы их реального существования.
Математические модели – это те модели, в которых при представлении процесса используются символы, а не физические устройства.
Очевидно, что модели могут принимать самые разные формы и записываться с разной степенью математической детализации. В повседневной практике при работе с системами пользуются умозрительными (субъективными) моделями, в которых математики нет вообще (это алгоритмы функционирования, правила управления системой и т.п.). Для описания свойств некоторых объектов и систем подходят числовые таблицы и (или) графики. Такие описания обычно называют графическими моделями (лин. системы автоматического управления САУ могут быть представлены своими импульсными реакциями, реакциями на единичный скачок или частотными характеристиками). В более сложных приложениях используются математические модели, в которых соотношение, описывающее связи между переменными объекта, задаются в виде определенных уравнений, поэтому такие модели иногда называют аналитическими моделями.
Существует 2 способа построения математических моделей:
1) моделирование или аналитический метод построения моделей;
|
|
|
2) идентификация.
Во втором способе построения моделей непосредственно используются экспериментальные данные. В этом случае ведется регистрация входных и выходных сигналов системы, и модель формируется в результате обработки соответствующих данных.
Классификация методов идентификаций.
В соответствии с современной теорией можно предложить следующую классификацию идентификаций:
1) по конечному результату идентификации: структурная и параметральная;
2) по способу изучения объекта идентификация: активная, пассивная;
3) по типу идентификационной модели:
· линейная и нелинейная,
· детерминированная и стохастическая,
· с непрерывным и дискретным временем,
· стационарная и нестационарная,
· одномерная и многомерная,
· статическая и динамическая,
· с сосредоточенными и распределенными параметрами.
Успех идентификации объекта существенно зависит от соотношения 2-ух факторов: объема априорной информации о структуре объекта и объема измерительной информации. Априорные сведения помогают определить структуру модели, т.е. ее вид (число входов и выходов, характер связи между ними). Эту процедуру называют идентификацией в широком смысле или структурной идентификацией.
При структурной идентификации объем априорной информации об объекте весьма ограничен, поэтому необходимо решить следующие задачи: выделение объекта из среды; задание класса моделей; определение характера связи между входом и выходом модели объекта; определение рационального числа информативных переменных (вх. и вых. объекта), учитываемых в моделях; определение возможности представления модели с требуемой точностью в классе линейных операторов; и др.
Для получения структуры модели существует 2 подхода:
1) теоретическое описание модели;
2) эксплуатационные методы.
Теоретическое описание модели – это наиболее полное описание, но требует больших знаний и высокой квалификации разработчика. Оно получается на основе физических законов, которым подчиняется данный процесс. Оно часто невозможно по нескольким причинам:
1) мы можем не знать всех физических законов;
2) теоретическая модель получается очень сложной и не поддается инженерным методам исследования.
|
|
|
В этом случае целесообразно использовать теоретико-экспериментальные методы построения моделей (используется только часть физических законов, а недостающая часть восполняется проведением экспериментов). Если применять часто экспериментальный метод построения модели, то модель получается имперической. Такая модель не является универсальной, она адекватно применима только в тех условиях, в которых были проведены эти эксперименты.
|
|
|


