 |
Регрессионный анализ. Пример построения математической модели процесса механообработки по экспериментальным данным.
|
|
|
|
Пусть задан некоторый стохастический объект, входная и выходная координата которого Х и Y являются случайными величинами.
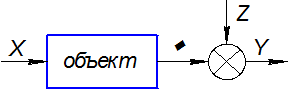
На Y влияет не только входная координата Х, но и случайная помеха Z (нестабильность режима работы объекта, стохастические воздействия среды, погрешности изменений Y и т.д.). Поэтому нельзя говорить о функциональной зависимости Y от Х. В подобных случаях следует говорить о наличии стохастической связи между переменными Х и Y объектов статики.
Случайные величины Х и Y являются зависимыми, если закон распределения вероятностей одной из них зависит от значения другой.
;
- условно интегральный закон распределения вероятностей;
- условная плотность распределения вероятностей;
Предположим, можно установить, что 
, тогда поведение сложной величины Y будет полностью характеризоваться условной плотностью распределения вероятностей 
.
Обозначим условные числовые характеристики Y:
- математическое ожидание;
- дисперсия;
, 
, 
, 
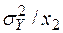
не зависит от х, а параметры функции плотности 
и 
зависит от того, какое значение х примет величина Х. Зависимость х называется регрессионной.
- регрессионная зависимость, показывает, как изменяется среднее значение Y при изменении Х. Если соединить плавными линиями точки, то получим линию регрессии. Эта линия есть статическая характеристика объекта.
Уравнением регрессии называют функцию f(x), описывающую линию регрессии. Уравнения регрессии классифицируют на линейные и нелинейные. При построении регрессионной модели объекта широко применяется пассивный метод идентификации.
Этот метод применяют при изучении статики объекта, уравнений помех, а также в тех случаях, когда недопустимы величины исходных возмущений на входе объекта. Пассивный метод идентификации основан на получении статической информации об объекте по данным его нормальной эксплуатации. Затем реализация входных х и выходных y величин обрабатываются т.о., чтобы определить регрессивную модель.
|
|
|
, где 
- вектор коэффициентов модели.
Определение уравнения регрессии состоит из 2 этапов:
1. выбор типа уравнения регрессии – осуществляется либо путем эмпирического выбора типа уравнения регрессии по виду корреляционного поля между входными и выходными величинами, либо путем теоретического изучения закономерности физического процесса, отражением которого является стохастическая связь между этими величинами. Иногда оба подхода используются в сочетании друг с другом.
2. расчет коэффициентов уравнения регрессии – чаще всего выполняется методом наименьших квадратов.
Следует отметить, что пассивный статический метод имеет ряд существенных недостатков по сравнению с активным методом:
1.получение модели объекта справедливо только в пределах используемого экспериментального статического материала.
2.трудно разделить эффекты от корреляции части входных величин многомерного объекта.
3.индивидуальные коэффициенты регрессии не имею какого-либо физического смысла.
4.не извлекается информация об ошибке опыта.
5.требуется получить большой объем экспериментальных данных и производить трудоемкие вычисления.
Указанные недостатки в значительной степени снижают ценность модели, полученной пассивным методом. К этому методу прибегают только в тех случаях, когда другие методы не могут быть использованы.
Предварительный анализ экспериментального статического материала составляет основную задачу корреляционного анализа при идентификации стохастического объекта. При этом суть корреляционного анализа сводится к оценке силы стохастической связи между случайными величинами Х и Y и по установлению вида зависимости между ними в виде уравнения регрессии. Чтобы предварительно определить наличие характерной связи между Х и Y наносят экстремальные точки 
и 
. На графике строят корреляционное поле.
|
|
|
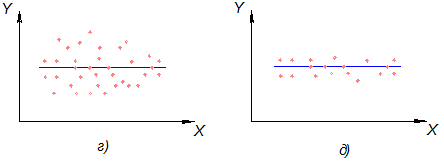
а-сильноотрицательная корреляция
б-сильноположительная корреляция
в-слабоположительная корреляция
г,д-отсутствие корреляции
По тесноте группирования точек вокруг прямой возможно судить о корреляционной связи.
Корреляционное поле характеризует вид связи между Х и Y, т.е. наличие линейной и нелинейной зависимости:
Существует 3 вида корреляции:
1)линейная;
2)нелинейная;
3)множественная;
При линейной корреляции линейная регрессия апраксимируется уравнением прямой, при нелинейной – уравнением кривой. Множественная корреляция определяет связь между многими величинами и при этом используется уравнение множественной регрессии. Наиболее распространенной является линейная корреляция. Понятие корреляции дает возможность судить о том, насколько тесно находятся экспериментальные точки на апраскимированной кривой линии регрессии.
Если регрессия определяет предполагаемые соотношения между переменными, то корреляция показывает, насколько хорошо это соотношение отражает действительность.
Задача стохастического объекта ставится таким образом: по данным выборки объема n оценить силу (тесноту) корреляционной связи между Х и Y, найти уравнение регрессии и оценить допустимую ошибку.
|
|
|
