И начала теории вероятностей

Комбинаторика

 

Горно-Алтайск 2007

 

 

Деев М.Е., Соловьев С.П., Соловьева Л.А. Комбинаторика и начала теории вероятностей. – Горно-Алтайск, 2007.

 

Настоящее пособие подготовлено для учащихся и преподавателей лицеев, гимназий, школ и классов с углубленным изучением математики для проведения факультативов и спецкурсов

 

 

Составители:

Деев М.Е., канд. физ.-мат. наук, доцент Горно-Алтайского государственного университета;

Соловьев С.П., канд. физ.-мат. наук, доцент Горно-Алтайского государственного университета;

Соловьева Л.А., старший. преподаватель Горно-Алтайского государственного университета.

 

 

ã Горно-Алтайский госуниверситет

ВВЕДЕНИЕ…………………………………………………………. Раздел I. Комбинаторика 1. Общие правила комбинаторики…………………………………. 2. Размещения……………………………………………………….. 3. Перестановки……………………………………………………... 4. Сочетания…………………………………………………………. 5. Треугольник Паскаля. Бином Ньютона………………………… 6. Примеры более сложных задач на сочетания, размещения и перестановки без повторений…………………….. 7. Перестановки с повторениями…………………………………... 8. Размещения с повторениями…………………………………….. 9. Сочетания с повторениями………………………………………. 10. Схема определения вида комбинации………………………… 11. Примеры более сложных задач комбинаторики……………… 12. Задачи для самостоятельного решения………………………... Раздел II. Теория ВЕРОЯТНОСТЕЙ 13. Классическое определение вероятности………………………. 14. Статистическое определение вероятности……………………. 15. Геометрические вероятности…………………………………... 16. Сумма событий…………………………………………………. 17. Произведение событий…………………………………………. 18. Вероятность суммы совместимых событий…………………... 19. Условные вероятности…………………………………………. 20. Вероятность произведения зависимых событий……………… 21. Формула полной вероятности………………………………….. 22. Формула Байеса…………………………………………………. 23. Формула Бернулли……………………………………………… 24. Случайные величины…………………………………………… 25. Числовые характеристики случайной величины……………... 26. Задачи для самостоятельного решения……………………….. ЛИТЕРАТУРА………………………………………………………. Ответы к задачам для самостоятельного решения………………..

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

 

Представителям самых различных специальностей часто приходится решать задачи, связанные с составлением и подсчетом числа различных комбинаций из чисел, букв и иных объектов. Такого типа задачи называются комбинаторными задачами, а раздел математики, изучающий вопросы о том, сколько различных комбинаций того или иного вида можно составить из данных элементов – комбинаторикой. Комбинаторика имеет большое значение для теории вероятностей, теории управляющих систем, статистики и других разделов науки и техники.

Комбинаторика возникла в XVI веке. Первоначально она, как и теория вероятностей, применялась для расчета шансов на выигрыш в различных азартных играх: рулетке, игре в кости, а также в карточных играх. Теоретические исследования вопросов комбинаторики предпринимали итальянские математики Тарталья и Кардано, французы Паскаль и Ферма, причем в работах последних были уже заложены основы теории вероятностей. Постепенно комбинаторные методы стали тем аппаратом, с помощью которого удалось получить замечательные результаты в теории вероятностей. Здесь можно отметить работы Я. Бернулли, который комбинаторными методами доказал первую содержательную теорему теории вероятностей – так называемый закон больших чисел. Серьезный вклад в разработку теории вероятностей сделали русские и советские математики П.Л. Чебышев, А.А.Марков, А.М.Ляпунов, А.Н.Колмогоров и другие. И хотя ее аппарат чрезвычайно расширился и усложнился по сравнению с аппаратом теории вероятностей XIX века, комбинаторные методы сохраняют свое значение и сегодня.

 

 

Раздел I. Комбинаторика

 

1. Общие правила комбинаторики

Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы и правилом произведения. Прежде всего определимся в терминологии. Если имеется, к примеру, 5 шаров в ящике, то мы будем говорить, что один шар из ящика можно выбрать пятью способами.

Правило суммы. Если объект А можно выбрать n способами, а объект В – k способами, то объект «А или В» можно выбрать n+k способами.

Пример 1. В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?

Решение. Здесь предполагается, что цветной шар – это синий или красный, поэтому надо применять правило суммы. Цветной шар можно выбрать 7 + 2 = 9 способами.

Правило произведения. Если объект А можно выбрать n способами, а объект В независимо от него – k способами, то пару объектов «А и В» можно выбрать n×k способами.

Пример 2. Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? (Игральная кость – это кубик, на гранях которого нанесены числа 1, 2, 3, 4, 5, 6)

Решение. На первой кости может выпасть 1, 2, 3, 4, 5 или 6 очков, то есть всего будет 6 вариантов. Точно так же и на второй кости 6 вариантов. По правилу произведения получится всего 6 × 6 = 36 способов.

Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов. Приведем еще несколько примеров, в которых необходимо выбрать правило суммы или произведения.

Пример 3. Из города А в город В ведут 5 дорог, а из города В в город С – 3 дороги. Сколькими способами можно проехать из города А в город С?

Решение. Чтобы проехать из А в С, надо проехать из А в В и из В в С, поэтому применим правило произведения. 5 × 3 = 15.

Пример 4. На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки одну книгу по математике?

Решение. Книга по математике – это книга по алгебре или по геометрии. Применяем правило суммы. 3 + 4 = 7.

Пример 5. В меню имеется 4 первых блюда, 3 вторых и 2 третьих. Сколько различных полных обедов можно из них составить?

Решение. Полный обед состоит из первого, и второго, и третьего блюд. По правилу произведения получаем 4 × 3 × 2 = 24 различных полных обеда.

 

2. Размещения

 

Если из данного множества предметов мы будем выбирать некоторое подмножество, то его будем называть выборкой. Выборки бывают упорядоченные и неупорядоченные. В упорядоченной выборке существенен порядок, в котором следуют ее элементы, другими словами, изменив порядок элементов, мы получим другую выборку. Например, из цифр 1, 2, 3, 4, 5 составляем трехзначные числа 123, 431, 524, …и т.д. Это упорядоченные трехэлементные выборки, ведь 123 и 132 – разные числа. Другой пример: из 20 учащихся класса будем выбирать двух дежурных. Любая пара дежурных представляет собой неупорядоченную двухэлементную выборку, так как порядок их выбора не важен.

Определение 2.1. Размещениями из n элементов по m (m £ n) называются упорядоченные m -элементные выборки из данных n элементов.

Из определения следует, что размещения отличаются друг от друга либо самими элементами, либо их порядком.

Число размещений из n по m обозначается 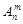. Чтобы вывести формулу числа размещений, заметим, что первый элемент в выборку мы можем выбрать n способами, второй из оставшихся n –1 элементов (n –1) способами, третий – (n –2) способами и так далее, m -й элемент можно выбрать n –(m –1) = n – m +1 способами. По правилу произведения получим:

(2.1)

Это и есть формула для вычисления числа размещений.

Найдем, например, число размещений из 7 по 3. Здесь n = 7, n – m +1 =5. Значит, 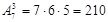. Заметим, что верхний индекс 3 показывает, сколько сомножителей надо взять в произведение. Приведем еще несколько примеров:

Пример 6. Составить все размещения из трех букв А, В, С по две буквы.

Решение. Это будут: АВ, АС, ВС, ВА, СА, СВ. Проверим по формуле: Их действительно 6 штук. Отметим, что АВ и ВА – разные размещения.

Пример 7. На пяти карточках написаны числа 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно из них составить?

Решение. Трехзначные числа представляют собой трехэлементные выборки из пяти цифр, причем, выборки упорядоченные, поскольку порядок цифр в числе существенен. Значит, этих чисел будет столько, сколько существует размещений из пяти элементов по 3.

. Ответ: 60 чисел.

Часто формулы комбинаторики записывают с помощью факториалов. Произведение всех последовательных натуральных чисел от 1 до n обозначается n! (читается: эн-факториал).

n! = 1 × 2 × 3 × … × n.

Формулу (1.1) можно теперь преобразовать следующим образом. Умножим и разделим правую часть этой формулы на выражение (n–m)! = 1 × 2 × 3 × … ×(n – m). Тогда получится:

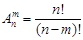(2.2)

Вычислим, например, по этой формуле:

Мы видим, что здесь приходится еще сокращать дробь, поэтому для вычисления числа размещений с конкретными значениями m и n первая формула предпочтительнее. Условились считать, что 0! =1.

 

3. Перестановки

 

Определение 3.1. Перестановками из n элементов называются размещения из n элементов по n.

Из определения следует, что в данном случае в упорядоченную выборку входят все n элементов и отличаться выборки могут только порядком. Поэтому все перестановки имеют один и тот же состав и отличаются только порядком элементов.

Число перестановок из n элементов обозначается Р_n. Подставляя в формулу (2.1) или (2.2) m = n, получим формулу для вычисления числа перестановок из n элементов:

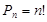(3.1)

Приведем несколько примеров использования этой формулы.

Р₅ = 5! = 1× 2 ×3 × 4 ×5 = 120; Р₂ = 2! = 1× 2 = 2; Р₁ = 1! = 1.

Пример 8. Составить все размещения из трех букв А, В, С.

Решение. АВС, АСВ, ВАС, ВСА, СВА, САВ. Проверим по формуле: Р₃ = 1× 2 ×3 = 6.

Пример 9. Сколькими способами можно расставить 7 книг на книжной полке?

Решение. Каждая расстановка будет отличаться от другой порядком следования книг. Поэтому это будут перестановки из семи элементов.

Р₇ = 7! = 1× 2 ×3 × 4 ×5 ×6 ×7 = 5040. Ответ: 5040 способами.

Пример 10. Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

Решение. Из данных шести цифр можно составить Р₆ = 6! = 720 перестановок. Но числа, начинающиеся на нуль, не являются шестизначными. Такие числа отличаются друг от друга перестановкой пяти остальных цифр, значит, их будет Р₅ = 120. Поэтому шестизначных чисел будет 720 – 120 = 600. Ответ: 600 чисел.

 

4. Сочетания

 

Определение 4.1. Сочетаниями из n элементов по m (m £ n) называются неупорядоченные m -элементные выборки из данных n элементов.

Ясно, что все сочетания отличаются друг от друга хотя бы одним элементом, а порядок элементов здесь не существенен. Число сочетаний из n по m обозначается . Чтобы из сочетаний получить размещения, надо упорядочить каждую m -элементную выборку, а это можно сделать m! способами. Следовательно, число сочетаний меньше числа размещений 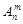в m! раз. Учитывая этот факт, из формул (2.1) и (2.2) получим соответствующие формулы для вычисления числа сочетаний:

(4.1)

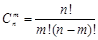и (4.2)

Например,

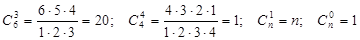
Пример 11. Составить все сочетания из трех букв А, В, С по две буквы.

Решение. Это будут АВ, АС, ВС. Проверим по формуле:

(Обратите внимание, что АВ и ВА – это одно и то же сочетание, на разные размещения.)

Пример 12. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать?

Решение. Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов – это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.

Ответ: 190 способами.

Пример 13. Сколькими способами можно группу из 15 учащихся разделить на две группы так, чтобы в одной группе было 4, а в другой – 11 человек?

Решение. Чтобы разделить эту группу, достаточно выбрать 4 человека из 15, а оставшиеся сами образуют другую группу. А выбрать 4 человека из 15 можно способами.

. Ответ: 1365 способами

Эту задачу можно было решить по-другому: из 15 учащихся выбрать 11, а остальные 4 образуют другую группу. Это можно осуществить способами.

.

Получается тот же ответ и возникает подозрение, что . Это действительно так. Сочетания обладают свойством

, (4.3)

в чем легко убедиться с помощью формулы (4.2):

.

Пользуясь этой формулой, вычислим .

 

5. Треугольник Паскаля. Бином Ньютона

Составим таблицу значений для n,m = 0, 1, 2, 3, 4, 5, 6, 7.

n m

 

Эту таблицу можно неограниченно продолжать вниз и вправо. Она называется треугольником Паскаля. Еще удобнее ее записывать в виде равнобедренного треугольника.

 

Такой треугольник Паскаля обладает свойством: каждое число равно сумме двух чисел, стоящих над ним, поэтому таблицу можно без труда продолжать вниз, не прибегая к вычислению числа сочетаний.

Нам знакомы формулы:

(a + b)¹ = a + b;

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Легко заметить, что коэффициенты в правых частях этих формул взяты из соответствующих строк треугольника Паскаля. Оказывается, при любом натуральном n справедлива формула

, (4.4)

которая называется формулой Ньютона в честь английского физика и математика Исаака Ньютона. Правую часть формулы (4.4) называют разложением степени бинома. По этой же формуле вычисляется (а – b)ⁿ, полагая (а – b)ⁿ = (a +(– b))ⁿ. В этом случае второе слагаемое будет со знаком минус, далее знаки чередуются.

Пример 14. Записать разложение 4-й степени бинома (а + b)⁴.

Решение. Коэффициенты разложения берем из 4-й строки треугольника Паскаля и используем формулу Ньютона:

(а + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

Пример 15. Записать разложение (2m –3n)⁵.

Решение. Используем 5-ю строку треугольника Паскаля.

(2m –3n)⁵ = (2m)⁵– 5(2m)⁴3n + 10(2m)³(3n)² –10(2m)²(3n)³ + 5(2m)(3n)⁴–

– (3n)⁵ = 32m⁵ – 240m⁴n + 720m³n² – 1080m²n³ + 810mn⁴ – 243n⁵.

Пример 16. Вычислить без калькулятора:

.

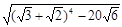Решение. Сначала возведем в четвертую степень двучлен.

. Поэтому

. Ответ: 7.

 

6. Примеры более сложных задач на сочетания, размещения и перестановки без повторений.

Пример 17. Из 10 роз и 8 георгинов нужно составить букет так, чтобы в нем было 2 розы и 3 георгина. Сколькими способами это можно сделать?

Решение. Выберем сначала из 10 роз 2 розы. Это можно осуществить 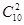способами. Мы используем сочетания, а не размещения, потому что порядок, в котором выбираются цветы, значения не имеет. Независимо от выбора роз 3 георгина из 8 можно взять способами. Тогда, по правилу произведения, 2 розы и 3 георгина можно выбрать способами.

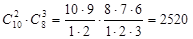. Ответ: 2520 способами.

Пример 18. Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной комиссии. Сколько существует возможностей выбора этих пяти человек?

Решение. Выберем сначала председателя и секретаря. Вариантов выбора этих двух человек из 40 будет . Размещения здесь потому, что этот выбор зависит от порядка, например, «Иванов – председатель, Петров – секретарь» и «Петров – председатель, Иванов – секретарь» – это разные варианты. Затем из оставшихся 38 человек изберем 3 человека в редакционную комиссию. Это делается способами. По правилу произведения всего вариантов:

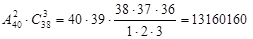
Можно было действовать иначе: сначала выбрать комиссию способами, а затем председателя и секретаря способами. Всего вариантов: . Ответ: 13160160

Пример 19. Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома:

а) стояли рядом;

б) не стояли рядом?

Решение. а). Подсчитаем сначала число вариантов расстановки, когда первый и второй тома стоят рядом. Их можно считать за одну книгу. Тогда получается Р₇ = 7! перестановок. Но первый и второй тома можно соединить двумя способами: слева первый, справа второй том и наоборот. За счет этого количество вариантов удваивается и всего их будет 2×7! = 10080.

б). Указанные тома не стоят рядом во всех остальных случаях, значит, из общего числа перестановок восьми книг надо вычесть число перестановок, когда тома стоят рядом. Итак, 8! – 10080 = 30240.

Ответ: а)10080, б) 30240.

Пример 20. Даны две параллельные прямые. На одной из них имеется 10 точек, а на другой – 20. Сколько существует треугольников с вершинами в данных точках?

Решение. Заметим, что здесь будет два типа треугольников, расположенных вершинами вверх и вершинами вниз. Для треугольника первого типа вершину выбираем 10 способами, а основание (2 точки из 20) – способами. Всего, по правилу произведения, получается 10× треугольников. Аналогично, треугольников второго типа будет 20× 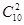. Наконец, применив правило суммы, получим общее количество треугольников: 10× + 20× 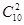= 2800.

Ответ: 2800 треугольников

Пример 21. В вагоне электрички имеются два противоположных дивана по 5 мест на каждом. Из 10 пассажиров четверо желают сидеть лицом по ходу движения, трое – против хода, а остальным безразлично, как сидеть. Сколькими способами могут разместиться пассажиры с учетом их желаний?

Решение. Желающих сидеть по ходу движения разместим способами, против хода – 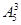, остальных троих на три пустых места – Р₃ = 3! способами. По правилу произведения всех пассажиров можно разместить способами.

Ответ: 43200 способами

Пример 22. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

Решение. Четырех девушек можно выбрать способами. После этого выбираем способами юношей (здесь уже существенен порядок). Всего = 17 417 400.

Ответ: 17 417 400 способами

 

7. Перестановки с повторениями

До сих пор мы рассматривали комбинации, в которых элементы не повторялись, то есть каждый из них можно было взять в выборку только один раз. Если же это ограничение убрать, то получим еще три вида комбинаций: перестановки, размещения и сочетания с повторениями.

Рассмотрим, например, слово «квант», состоящее из пяти различных букв. Если менять порядок букв, получим 5! =120 перестановок, т.е. 120 новых слов. (Словом будем называть любую комбинацию букв). Если проделать то же со словом «АТАКА», то перестановок будет меньше, потому что, меняя местами первую, третью и пятую буквы, будем получать то же самое слово. И, так как три буквы «А» можно менять местами 3! = 6 способами, то и перестановок в слове «АТАКА» будет в 6 раз меньше.

А теперь рассмотрим общий случай. Пусть дана выборка

,

состоящая из n элементов, причем, элемент а повторяется m ₁ раз, элемент b – m ₂ раз, и т.д., элемент с – m _k раз и m ₁ + m ₂ +…+ m _k = n. Перестановки в такой выборке, где есть одинаковые элементы, называются перестановками с повторениями и число перестановок с повторениями обозначается 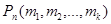. Из приведенных выше рассуждений следует формула:

(7.1)

Пример 23. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?

Решение. Первая линия шахматной доски представляет собой 8 клеток, на которых и надо расположить эти 8 фигур. Различные варианты расположения будут отличаться только порядком фигур, значит, это будут перестановки с повторениями Р₈ (2,2,2). По формуле:

Ответ: 5040 способами

Пример 24. У мамы 2 яблока, 3 груши и 4 апельсина. Каждый день в течение девяти дней она выдает сыну по одному фрукту. Сколько может быть вариантов такой выдачи?

Решение. Обозначая фрукты по первым буквам названия, составим несколько вариантов выдачи: ЯЯГГГАААА, ААГГЯГААЯ, ГГГААЯЯАА. Эти выборки имеют один и тот же состав и отличаются только перестановкой элементов, поэтому применяем формулу числа перестановок с повторениями.

Ответ: 1260 вариантов

 

8. Размещения с повторениями

Определение.8.1. Размещениями с повторениями из n по m называются упорядоченные m -элементные выборки, в которых элементы могут повторяться.

Число размещений с повторениями из n по m обозначается В отличие от обычных размещений, где m £ n, в размещениях с повторениями m и n могут быть любыми. Выведем формулу числа размещений с повторениями. Будем конструировать m -элементную выборку из n элементов.Первый элемент, как и все последующие, мы можем выбирать n способами, ведь на любое место можно поставить любой из n элементов. Применяя правило произведения, получим:

(8.1)

Пример 25. Сколько четырехбуквенных «слов» можно составить из букв «М» и «А»? Результат проверить непосредственно.

Решение. Составим несколько таких «слов». МММА, МАМА, МААА …Мы видим, что состав выборки меняется, порядок элементов в выборке существенен. Значит, это – размещения с повторениями из 2 букв «М» и «А» по 4 буквы.

Выпишем непосредственно все эти 16 «слов»:

ММММ, МММА, ММАМ, МАММ, АМММ, ММАА, МАМА, АММА, АМАМ, ААММ, МААМ, АМАА, ААМА, АААМ, МААА, АААА.

Ответ: 16 слов

Пример 26. Вдоль дороги стоят 6 светофоров. Сколько может быть различных комбинаций их сигналов, если каждый светофор имеет 3 состояния: «красный», «желтый», «зеленый»?

Решение. Выпишем несколько комбинаций: КККЖЗЗ, ЗЗЗЗЗЗ, КЖЗКЖЗ… Мы видим, что состав выборки меняется и порядок элементов существенен (ведь если, например, в выборке КЖЗКЖЗ поменять местами К и Ж, ситуация на дороге будет другой). Поэтому применяем формулу размещений с повторениями из 3 по 6:

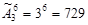Ответ: 729 комбинаций

 

9. Сочетания с повторениями

Определение 9.1. Сочетаниями с повторениями из n по m называются неупорядоченные m -элементные выборки, в которых элементы могут повторяться.

Число сочетаний с повторениями из n по m обозначается . В отличие от обычных сочетаний, где m £ n, в сочетаниях с повторениями m и n могут быть любыми. Формулу для вычисления числа сочетаний с повторениями выведем на основе следующего частного примера.

Пример 27. В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 5 открыток?

Ясно, что в купленном наборе открыток они будут повторяться и порядок их в наборе не важен, то есть это будут сочетания с повторениями из 3 по 5. Зашифруем все возможные наборы из 5 открыток следующим образом: открытки каждого вида изобразим в виде единиц, разделенных символами D. Так выборка 11D1D11 означает, что мы купили 2 открытки первого вида, одну – второго и 2 открытки третьего вида, а DD11111 – все 5 открыток третьего вида. Подсчитаем количество таких выборок. Каждая из них состоит из 7 элементов: пяти единиц и двух трегольников, то есть состав не меняется, а меняется только порядок элементов. Значит, это будут перестановки с повторениями из 7 элементов, где D повторяется два раза, а 1 – пять раз.

Ответ: 21способом

В общем случае, если имеется n видов открыток, а купить надо m штук, получим:

(9.1)

Это и есть формула числа сочетаний с повторениями, однако она неудобна для запоминания, поэтому представим эту формулу в другом виде. Для этого вычислим по формуле (4.2):

и сравним с (9.1). Правые части этих равенств равны. Приравнивая левые части, получим формулу, выражающую число сочетаний с повторениями через обычное число сочетаний.

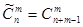(9.2)

Пример 28. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба?

Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ, …

Состав меняется от выборки к выборке, значит, это уже не перестановки; порядок элементов несущественен, это – сочетания с повторениями из 2 по 6.

.

Сделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7.

Ответ: 7 вариантов

Пример 29. Сколько существует прямоугольных параллелепипедов, длина ребра которых выражается целым числом от 1 до 9?

Решение. Параллелепипед определяется тремя ребрами, поэтому его можно представить в виде тройки чисел. Выпишем несколько вариантов: (1,1,5); (2,7,9); (4,4,4) … Элементы в выборке могут повторяться, состав меняется, порядок не существенен, например, выборки (2,7,9) и (9,2,7) соответствуют одному и тому же параллепипеду. Применяем формулу сочетаний с повторениями

Ответ: 165 параллелепипедов

 

10. Схема определения вида комбинации

Приведем в систему полученные формулы всех 6 видов комбинаций с повторениями и без повторений, представив алгоритм определения вида комбинации следующей схемой.

 

 

 

да нет

 

 

да нет нет да

	Существенен ли порядок?		Существенен ли порядок?

 

 

 

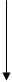да нет нет да

 

 

 

 

Решим несколько задач с применением данной схемы.

Пример 30. В магазине игрушек имеются 7 одинаковых Чебурашек и 2 одинаковых Крокодила. Сколькими способами их можно расставить в один ряд на витрине?

Решение. Обозначив игрушки первыми бувами названия, составим несколько комбинаций: КЧЧЧЧЧЧЧК, ЧЧЧКЧКЧЧЧ, ККЧЧЧЧЧЧЧ, … Повторяются ли элементы в выборке? Да. Меняется ли состав? Нет, ведь каждая выборка состоит из семи букв «Ч» и двух букв «К». Следовательно, это перестановки с повторениями.

. Ответ: 36 способами

Пример 31. На окружности расположено 20 точек. Сколько существует вписанных треугольников с вершинами в этих точках?

Решение. Занумеруем точки числами от 1 до 20. Тогда каждый вписанный треугольник будет представлять собой тройку чисел. Выпишем несколько выборок: (1, 5, 19), (15, 2, 9), (14, 13, 7) …. Числа в выборке не могут повторяться, так как все вершины треугольника различны. Состав меняется от выборки к выборке, порядок не существенен, так как (1, 5, 19) и (19, 5, 1) – один и тот же треугольник. По схеме получается, что это сочетания без повторений из 20 по 3.

Ответ: 1140 треугольников

Пример 32. В некотором сказочном государстве не было двух жителей с одинаковым набором зубов (либо у них разное число зубов, либо зубов нет в разных местах). Оцените наибольшую численность населения этого государства, если максимальное число зубов у человека – 32.

Решение. Закодируем каждого жителя набором из 32 нулей и единиц. Единица соответствует наличию зуба в данном месте, нуль – его отсутствию. Выпишем несколько комбинаций: 11111…11, 1010…11, 00000…00, …Элементы повторяются, состав меняется, порядок существенен. Это – размещения с повторениями из 2 по 32.

. Ответ: 4294967296 жителей

Пример 33. Имеются в неограниченном количестве палочки длиной 5, 6, 7, 8, 9, 10 сантиметров. Сколько различных треугольников можно из них составить?

Решение. Составим несколько выборок: (5,5,5); (6,7,8); (8,9,9)..

Элементы повторяются, состав меняется, порядок не существенен. Согласно схеме, применяем формулу сочетаний с повторениями из 6 по 3: . Однако, здесь есть небольшой подвох: треугольника со сторонами 5, 5, 10 не существует, так что их будет 55.

Ответ: 55 треугольников

 

11. Примеры более сложных задач комбинаторики

Пример 34. Выпуклый многоугольник имеет 90 диагоналей. Сколько у него сторон?

Решение. Обозначим количество сторон многоугольника через n. Вершин у него тоже будет n. Соединим вершины попарно отрезками, которых будет . Среди этих отрезков будет n сторон, остальные – диагонали. Составим уравнение по условию задачи: , . Отсюда получается квадратное уравнение , корни которого . По смыслу задачи подходит .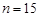

Ответ: 15 сторон

Пример 35. Сколько шахматистов участвовало в турнире, если каждый участник сыграл с каждым по одной партии, а партий было сыграно в 10 раз больше числа участников.

Решение. Если участников – n человек, партий будет сыграно штук. Составим уравнение , решив которое, найдем:

n =21. Ответ: 21 шахматист

Пример 36.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: