 |
Вероятность произведения зависимых событий
|
|
|
|
Пусть даны два зависимых события А и В. И из n равновозможных исходов событию А благоприятствуют m, событию В – k, событию АВ – r исходов (r£ m, r£ k).
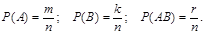
Если произошло событие А, то реализовался один из m исходов, благоприятствующих А. Вероятность того, что при этом условии произошло событие В найдется, как условная вероятность
. Отсюда 
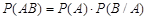. Это и есть правило умножения зависимых событий.
Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло.
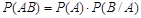(20.1)
Формула полной вероятности
Пусть нам требуется найти вероятность события А, которое происходит вместе с одним из попарно несовместимых событий Н1, Н2, …, Нn, образующих полную группу. События Н1, Н2, …, Нn будем называть гипотезами. Имеем А = АН1 + АН2 + … + АНn, причем АН1, АН2, … АНn попарно несовместимы. Применяя формулы (16.1) и (20.1), получим:
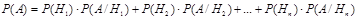(21.1)
Это есть формула полной вероятности. С ее помощью решается широкий класс задач.
Пример 48. Имеются 3 одинаковых коробки, содержащие по 20 лампочек. В 1-й коробке из них 2 бракованные лампочки, во второй – 4, в третьей – 5. Наугад выбирается коробка, а из нее наугад одна лампочка. Какова вероятность, что эта лампочка бракованная?
Решение. А: «Взята бракованная лампочка». Возникают 3 гипотезы: Н 1: «Выбрана 1-я коробка», Н 2: «Выбрана 2-я коробка», Н 3: «Выбрана 3-я коробка». Поскольку все коробки одинаковые, 
. Находим условные вероятности.
По формуле полной вероятности
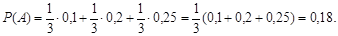
Ответ: 0,18
Пример 49. Из полного набора костей домино извлечена одна кость. Найти вероятность того, что вторую наугад извлеченную кость можно приставить к первой согласно правилам игры.
|
|
|
Решение. А: «Вторую кость можно приставить к первой». Если первая кость окажется дублем, вероятность события А будет меньше, чем если бы она была не дублем. Поэтому возникают две гипотезы: Н 1: «Первая кость – дубль», Н 2: «Первая кость – не дубль». Находим: 
. Если первая кость – дубль, то найдутся 6 из 27 оставшихся костей, которые можно приставить к первой, а если не дубль, то их будет 12. Поэтому
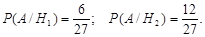По формуле полной вероятности
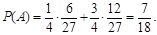Ответ: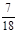 
Формула Байеса
В тесной связи с формулой полной вероятности находится формула Байеса. Она относится к той же ситуации, когда событие А наступает только вместе с одной из гипотез и позволяет оценить вероятность гипотезы после того, как событие А произошло.
Пусть произведен опыт и наступило событие А. Мы не можем с точностью сказать, какая из гипотез осуществилась, однако можем найти вероятность каждой из них. По формуле (20.1)
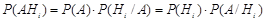. Отсюда
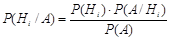(22.1)
Это и есть формула Байеса. Здесь Р(А) находится по формуле полной вероятности, Hi (i = 1, 2, …, n) – любая из гипотез, а Р(Нi/А) – вероятность этой гипотезы при условии, что произошло событие А.
Пример 50. В трех одинаковых ящиках находятся 6 белых и 4 черных, 7 белых и 3 черных, 8 белых шаров соответственно. Из произвольного ящика наугад выбирается один шар. Он оказался белым. Какова вероятность, что этот шар вынут из второго ящика?
Решение. Пусть Н1, Н2, Н3 – три гипотезы, что выбран 1-й, 2-й, 3-й ящик. Требуется найти вероятность второй гипотезы при условии, что событие А произошло, т.е.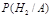 
. По формуле Байеса
=
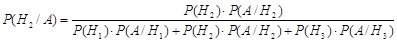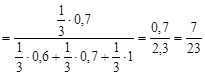. Ответ: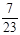 
Формула Бернулли
Пусть проводится n независимых испытаний, в каждом из которых с одной и той же вероятностью p может появиться некоторое событие А. Поставим задачу: найти вероятность того, что в этих n испытаниях событие А появится ровно m раз. Обозначим А 1 – появление события А в 1-м испытании, А 2 - во 2-м испытании, и так далее. Непоявление события А в 1-м испытании обозначим 
, во 2-м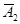 
и т.д. Событие, состоящее в появлении события А m раз в n испытаниях представится в виде суммы произведений вида 
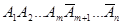. Если обозначить вероятность непоявления события А через q,то вероятность каждого такого произведения равна 
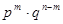, а всего их будет 
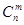штук. Получим:
|
|
|
(23.1)
Это – формула Бернулли. Здесь обозначено: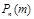 
вероятность появления события А m раз в n испытаниях, р – вероятность появления события А в одном испытании, q = 1 – p.
Пример 51. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность пяти попаданий при шести выстрелах.
Решение. n =6, m =5, p =0,8, q = 1 – 0,8 = 0,2.
Ответ: 0,39
Пример 52. Вы играете в шахматы с равным по силе партнером. Чего следует больше ожидать: 3 побед в 4 партиях или 5 побед в 8 партиях?
Решение. р = 0,5; q = 0,5.
,
.
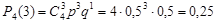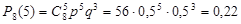Ответ: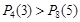 
Случайные величины
Очень часто в результате опыта в качестве случайного события появляется некоторое число. Так при бросании игральной кости выпадает определенное число очков, при обследовании партии готовых деталей обнаруживается некоторое число бракованных и т.д.
Определение 24.1. Случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, заранее неизвестно, какое именно.
Приведем несколько примеров случайных величин.
1.Приобретено несколько лотерейных билетов. Х – количество выигравших билетов.
2.Испытывается электрическая лампочка на длительность горения. Х – время горения до выхода из строя.
3.Число автомобилей, проезжающих по улице за 1 час.
Если количество возможных значений случайной величины конечно, она называется дискретной, а если возможные значения заполняют некоторый числовой промежуток, то – непрерывной.
Так в приведенных выше примерах 1 и 3 случайные величины – дискретные, а в примере 2 – непрерывная. Для полного описания случайной величины недостаточно знать, какие значения она принимает, необходимо еще оценить, как часто она принимает то или иное значение. Для изучения дискретной случайной величины составляют так называемый закон распределения. Это таблица, в которую занесены все возможные значения случайной величины и их вероятности. В качестве примера составим закон распределения случайной величины Х – суммы очков при однократном бросании двух игральных костей.
|
|
|
| Х | |||||||||||
| Р |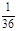 
| 
| 
| 
| 
| 
|
|
|
|
|
|
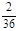
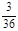
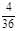
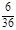
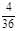
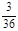
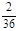
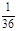
Если закон распределения составлен правильно, сумма вероятностей всех значений должна равняться 1.
|
|
|
