Задачи для самостоятельного решения

44. Игральная кость брошена 1 раз. Какова вероятность, что выпало: а) 3 очка?; б) менее 5 очков?; в) не более 3 очков?; г) нечетное число очков?; д) число очков, кратное трем?; е) менее 8 очков?

45. Участники жеребьевки тянут из ящика наугад жетоны, на которых написаны натуральные числа от 1 до 100. Какова вероятность, что номер наугад взятого жетона не содержит цифры 5?

46. На четырех карточках написаны буквы О, М, Т, С. Они перемешиваются и наугад раскладываются в ряд. Какова вероятность, что получилось слово «МОСТ»?

47. Студент выучил 25 экзаменационных вопросов из 30. Какова вероятность, что он не ответит на произвольно взятый вопрос?

48. Отделом технического контроля завода установлено, что 2% изготавливаемых деталей – бракованные. Найти вероятность того, что произвольно взятая с конвейера деталь является годной.

49. В урне 12 черных шаров и 4 белых. Наугад извлекаются 3 шара. Найти вероятность того, что все они – черные.

50. К концу дня в магазине осталось 20 арбузов, из которых 15 – спелые. Покупатель выбирает 2 арбуза. Какова вероятность, что хотя бы один из них спелый?

51. Два стрелка стреляют в одну и ту же мишень по одному разу. Вероятности их попадания соответственно равны 0,8 и 0,7. Найти вероятность того, что в мишени окажется ровно одна пробоина.

52. В комоде перемешаны 8 белых и 6 красных шнурков. Что вероятнее вытащить наугад: 2 красных или 3 белых?

53. Из колоды в 36 карт наугад выбирают 4 карты. Какова вероятность, что: а) все они – тузы?; б) все они – бубновой масти?

54. В игре «Спортлото» участник зачеркивает 5 номеров из 36. После розыгрыша объявляются 5 выигрышных номеров. Найти вероятность того, что игрок угадает 3 номера.

55. Баскетболист из 20 штрафных бросков в среднем забрасывает 16. Производится 1 бросок. Какова вероятность, что он промахнется?

56. Бросают две игральных кости. Найти вероятность того, что выпала: а) сумма очков, равная 7?; б) сумма очков, меньшая 6?

57. Из колоды в 36 карт игрок выбирает наудачу 4 карты. Какова вероятность, что все они – разных мастей?

58. В ящике т черных шаров и п белых. Наугад вынимаем т шаров. Найти вероятность того, что все они – черные.

59. В ящике а стандартных деталей и b бракованных. (b >1). Выбирают наугад 5 деталей. Какова вероятность, что ровно 2 из них – бракованные?

60. Найти вероятность выпадения трех гербов при бросании трех монет.

61. Вероятность для студента сдать экзамен равна 0,7, а сдать зачет – 0,8. Какова вероятность, что он не сдаст ни зачета, ни экзамена?

62. В комоде перемешаны 8 черных и 6 зеленых носков. В темноте, наугад надеваем два носка. Что вероятнее: что они – одного цвета или – разных цветов?

63. Три стрелка с вероятностями попадания 0,9; 0,8 и 0,7 стреляют в одну и ту же мишень по одному разу. Найти вероятность того, что в мишени окажется ровно 2 пробоины.

64. Два сильных студента выучили по 25 экзаменационных билета из 30, а слабый – только 10 билетов. Какова вероятность того, что слабый сдаст экзамен, а один из сильных – не сдаст?

65. Три охотника стреляют в кабана по одному разу. Вероятность того, что первый охотник поразит цель, равна 0,9, второй – 0,7, третий – 0,4. Вычислить вероятность того, что кабан будет убит.

66. В 1-й урне 8 белых и 6 черных шаров, а во второй – 4 белых и 2 черных. Из 1-й урны во вторую перекладывают один шар, а затем вынимают один шар из второй урны. Какова вероятность, что он – белый?

67. Студент выучил 25 экзаменационных билетов из 30. Когда вероятность сдать экзамен больше: если он идет брать билет первым или вторым?

68. Две машинистки печатают текст из 6 страниц, причем, первые 2 страницы печатает первая машинистка, а остальные 4 – вторая. Вероятность ошибки первой 0,1, а второй – 0,2. Найти вероятность того, что в тексте будет допущена ошибка?

69. На карточках написаны буквы, образующие слово «комбинаторика», но 2 карточки из этого набора утеряны. Наудачу извлекается одна карточка. Найти вероятность того, что на ней – гласная буква.

70. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность 5 попаданий при 6 выстрелах.

71. В семье 6 детей. Считая рождение мальчика и девочки равновероятными, найти вероятность того, что в этой семье 3 девочки и 3 мальчика.

72. В квартире 4 электролампочки. Для каждой из них вероятность того, что она останется исправной в течение года, равна . Какова вероятность, что в течение года придется заменить не менее половины лампочек?

73. Вероятность отказа каждого прибора при испытании равна 0,4. Что вероятнее: отказ двух приборов при испытании четырех или отказ трех из шести?

74. Монета подбрасывается 4 раза. Составить закон распределения случайной величины Х – числа появлений герба, найти математическое ожидание и дисперсию.

75. На пути автомобиля расположено 5 светофоров, каждый из которых пропустит его с вероятностью 0,6. Найти закон распределения случайной величины Х – числа светофоров до первой остановки машины.

ЛИТЕРАТУРА

 

1. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969.

2. Виленкин Н.Я. Комбинаторика. М. Мир. 1968.

3. Виленкин Н.Я. Индукция. Комбинаторика. М. Просвещение. 1976.

4. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1988.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. М.: Высшая школа, 1980.

6. Деев М.Е., Соловьев С.П. Элементы комбинаторики и теории вероятностей. Горно-Алтайск, 1992.

7. Лютикас В.С. Школьнику о теории вероятностей. М.: Просвешение, 1976.

8. Лютикас В.С. Факультативный курс по математике. Теория вероятностей. М.: Просвещение, 1990.

9. Румшиский Л.З. Элементы теории вероятностей. М.: Наука, 1966.

10. Солодовников А.С. Теория вероятностей. М.: Просвещение, 1983

 

Ответы к задачам для самостоятельного решения

1). 120; 2). 6; 3). 20; 4). 151200; 5). 56; 6). 81; 7). 600; 8). 78; 9). 128; 10). 80000; 11). 1860480; 12). 32; 13). 120; 14). 153; 15). 54, ; 16). 6; 17). 1320; 18). 40320; 19). 210; 20). 120; 21). 300; 22). 171100; 23). 16800; 24). а) 45; б) 60; в) 60; 25). 17; 26). 2970; 27). 500; 28). 1680; 29). 30; 30). 56; 31). 210; 32). 66; 33). 210; 34). 23!; 35). 80 млн.; 36). 1999; 37). 3612; 39). ; 41). 15; 42). а) 4; б) 3; в) {3,4}; г) {5,7}; 45). 0,81; 46). ; 47). ; 48). 0,98; 49). ; 50). 0,9375; 51). 0,38; 52). 2 красных; 53). а) 0,0000169; б) 0,002139; 54). 0,012; 55). 0,2; 56). а) ; б) ; 57). 0,037; 58). ; 59). ; 60). 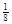; 61). 0,06; 62).разных; 63). 0,398; 64). 0,09; 65). 0,982; 66). ; 67).одинаково; 68). 0,16; 69). ; 70). 0,3932; 71). ; 72). ; 73). 2 из 4; 74). М(Х)=2; D(Х)=1; s(Х)=1.

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: