Числовые характеристики случайной величины

Пусть дискретная случайная величина Х имеет распределена по закону:

Х	x1	x2	x3	…	хn
р	p1	p2	p3	…	pn

 

Определение 25.1. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений возможных значений на их вероятности.

М(Х) = х₁р₁ + х₂р₂ + … + х_np_n (25.1)

Теоретико-вероятностный смысл этой характеристики состоит в том, что математическое ожидание приближенно равно среднему арифметическому всех ее значений при достаточно большом числе испытаний. Математическое ожидание обладает также следующими свойствами:

1.Математическое ожидание постоянной величины равно самой этой постоянной.

М(с) = с

2.Постоянный множитель можно выносить за знак математического ожидания.

М(сХ) = сМ(Х)

3. Математическое ожидание суммы двух случайных величин равно сумме их вероятностей.

М(Х + Y) = М(Х) + М(Y)

4. Математическое ожидание разности двух случайных величин равно разности их вероятностей.

М(Х – Y) = М(Х) – М(Y)

Математическое ожидание не дает полной характеристики закона распределения. Так, например, даны две случайных величины Х и Y следующими законами распределения:

X	–2				Y	–50
p	0,4	0,2	0,4		p	0,3	0,4	0,3

Математические ожидания их равны М(Х) = М(Y) = 0, однако возможные значения рассеяны по-разному: у случайной величины Y они сильнее отклоняются от среднего значения М(Y). И на практике, при одинаковой средней величине годовых осадков одна местность может быть благоприятной для земледелия, другая – нет.

Поэтому возникает необходимость введения новых числовых характеристик случайной величины, по которым можно судить о рассеянии возможных значений около математического ожидания. Этими характеристиками являются дисперсия D(X) и среднее квадратическое отклонение s.

Определение 25.2. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения.

D(X) = M[X –M(X)]² (25.2)

Определение 25.3. Средним квадратическим отклонением дискретной случайной величины Х называется квадратный корень из ее дисперсии.

(25.3)

Дисперсия обладает следующими свойствами, которые непосредственно получаются из формулы (25.2).

1.Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.

D(X) = M(X²) – M²(X) (25.4)

2.Дисперсия постоянной величины равна нулю.

D(c) = 0

3.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

D(cX) = c²D(X)

4.Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий.

D(X + Y) = D(X) + D(Y)

5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий.

D(X – Y) = D(X) + D(Y)

Пример 53. Испытывается устройство, состоящее из четырех одинаковых приборов. Вероятность отказа каждого прибора равна 0,2. Составить закон распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайного числа отказавших приборов.

Решение. Х – число отказавших приборов. Возможные значения этой случайной величины 0, 1, 2, 3, 4. Их вероятности находим по формуле Бернулли при n =4, p =0,2, q = 0,8.

Проверка: 0,4096 + 0,4096 + 0,1536 + 0,0256 + 0,0016 =1. Закон распределения будет иметь вид:

Х
р	0,4096	0,4096	0,1536	0,0256	0,0016

 

М(Х) = 0,4096× 0 + 0,4096× 1 + 0,1536× 2 + 0,0256× 3 + 0,0016× 4 = 0,8;

D(X) = М(Х²) – М²(Х) = 0,4096× 0² + 0,4096× 1² + 0,1536× 2² + 0,0256× 3² + 0,0016× 4² – 0,8² = 0,64; s(Х) = = 0,8.

Ответ: М(Х) = 0,8; D(X) = 0,64; s(Х) = 0,8

Пример 54. Круглая мишень разделена диаметрами на 8 равных секторов и вращается вокруг оси О. При достаточно большой скорости вращения стрелок не может различать секторы и вынужден стрелять наугад. При попадании в 1-й сектор он выигрывает 1 руб., во 2-й – выигрывает 2 руб. и т.д., при попадании в 8-й сектор – выигрывает 8 руб. Выгодно ли стрелку участвовать в такой игре, если за каждый выстрел надо платить 5 руб.?

Решение. Пусть случайная величина Х – размер выигрыша стрелка при одном выстреле. Так как все секторы одинаковы, вероятности попадания в каждый равны по 1/8. Найдем математическое ожидание выигрыша. М(Х) = 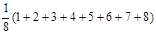= = 4,5 (руб.). Это среднее значение

выигрыша в данной игре, которое совпадает со «справедливой ценой» одного выстрела. Так как за выстрел приходится платить 5 руб., то стрелять много раз невыгодно.

Пример 55. У охотника 4 патрона. Он стреляет по зайцу, пока не попадет или пока не кончатся патроны. Составить закон распределения числа израсходованных патронов, если вероятность его попадания при одном выстреле равна 0,6. Найти М(Х), D(Х), s(Х).

Решение. Х – число израсходованных патронов. Возможные значения Х = 1, 2, 3, 4. Находим их вероятности.

Р(Х=1) = 0,6;

Р(Х=2) = 0,24;

Р(Х=3) = 0,4 × 0,4 × 0,6 = 0,096;

Р(Х=4) = 0,4 × 0,4 × 0,4 × 0,6 + 0,4 × 0,4 × 0,4 × 0,4 = 0,064.

Проверка: 0,6 + 0,24 + 0,096 + 0,064 = 1. Закон распределения Х:

Х
р	0,6	0,24	0,096	0,064

 

М(Х) = 0,6 × 1 + 0,24 × 2 + 0,096 × 3 + 0,064 × 4 = 1,624;

D(Х) = 0,6 × 1² + 0,24 × 2² + 0,096 × 3² + 0,064 × 4² – 1,624² = 0,81;

s(Х) = = 0,9.

Ответ: М(Х) = 1,624; D(Х) = 0,81; s(Х) = 0,9.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: