 |
Интервальные ряды динамики
|
|
|
|
Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции (за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.
Средний уровень в интервальных рядах динамики ( ) исчисляется по формуле средней арифметической простой:
) исчисляется по формуле средней арифметической простой:
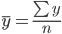
- y — уровни ряда (y1, y2 ,...,yn),
- n — число периодов (число уровней ряда).
Уi -1 - уровень периода, предшествующего текущему;
У0 - уровень, принятый за постоянную базу сравнения n- число уровней ряда;
t - продолжительность периода, в течение которого уровень не изменялся
Ц – епной
Б - базисный
уi — уровень сравниваемого периода;
| Абсолютный прирост | |

| 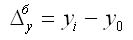
|
Коэффициент роста 
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.

Темп прироста можно получить из темпа роста:
 %
%
Коэффициент прироста 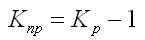
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:

укрупнение интервалов – это простейший метод сглаживания уровней ряда с целью выявить основную тенденцию их изменения. При этом для укрупненных интервалов определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда соответствуют коротким промежуткам времени.
Аналитическое выравнивание - наиболее совершенный способ определения тенденции развития в рядах динамик. При этом методе фактические ур-ни заменяются теоретическими илил расчетными.
|
|
|
1.. Средний уровень интервального ряда динамики определяется как средняя: Арифметическая
2. В практике статистики при расчете относительного показателя динамики используют следующие данные:
· Текущий уровень явления
· Предшествующий (базисный) уровень явления
3. Сбор бананов в Эквадоре в 2006 году составил 106,1% от уровня 2005 года. Данная величина является: Темпом роста
4. Средний уровень интервального ряда динамики определяется как:
Средняя арифметическая
5. Ряд динамики, характеризующий экспорт страны по каждому году за период с 2000 по 2006 годы, по виду относится: к интервальным рядам динамики.
6. По формуле игрек итое/ игрек итое минус один определяется:
Цепной коэффициент роста
7. Согласно теории статистики с относительным показателем динамики непосредственно связаны следующие показатели
· Относительный показатель плана
· Относительный показатель реализации плана
8. Стоимость основных средств предприятия на 1 января составила 10млн.руб., на 1февраля-12млн.руб, на 1марта-15млн. руб., на 1апреля-14млн.руб. Среднемесячная стоимость основных средств за квартал равна___ 10млн.руб.______
9. Отношение уровней ряда динамики называется:
Коэффициентом роста
ИНДЕКСНЫЙ МЕТОД
Индекс — представляет собой результат сравнения двух состояний одного явления.
Индексы — один из наиболее распространенных статистических показателей, используемый для экономических расчетов. Наиболее часто используются индексы, характеризующие изменение во времени, т.е. в этом случае индекс представляет собой показатель динамики.
С помощью индексов решаются следующие задачи:
- Определяются обобщающие показатели:
- обобщающие показатели динамики;
- территориальных сравнений;
- сравнение с планом.
- Изучение динамики средних величин: влияние структуры и структурных сдвигов на динамику средней величины.
- Изучение факторов в динамике сложных явлений:
- относительное влияние факторов на результат;
- абсолютный прирост результата в зависимости от динамики факторов.
Сравнение может проводиться по отдельным единицам совокупности и по совокупности единиц. В зависимости от этого различают индивидуальные и сложные индексы.
|
|
|
Если сравнение производится по отдельным единицам совокупности, имеем индивидуальный или элементарный индекс. Например, сравнение цены в разных магазинах на один и тот же товар (индивидуальный территориальный индекс), сравнение объема продаж картофеля на двух рынках, сравнение цен на картофель в сентябре по сравнению с маем (индивидуальный индекс цен) и т.д.
В каждом индексе выделяют 3 элемента:
- индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс
- сравниваемый уровень — это тот уровень, который сравнивают с другим.
- базисный уровень — это тот уровень, с которым производится сравнение.
Для расчета индекса необходимо найти отношение сравниваемого уровня к базисному и выразить его в виде коэффициента, если база сравнения приравнивается к единице, или в процентах, если база сравнения принимается за 100%. Обычно расчеты индексов производятся в форме коэффициентов с точностью до третьего знака после запятой, т. е. до 0,001, в форме процентов — до десятых долей процента, т.е. до 0,1%.
Для удобства построения индексов используется специальная символика:
- i — символ индексируемого показателя — индекс, характеризующий изменение уровня элемента явления.
- I — с подстрочным индексируемым показателем — для группы элементов или всей совокупности в целом.
- q — количество проданных товаров или произведенной продукции в натуральном выражении
- p — цена за единицу товара
- z — себестоимость единицы продукции
- w — производительность труда
- T — отработанное время или численность работников
- l — средняя заработная плата одного работника
- 0 — базисный период
- 1 — отчетный период
Математически элементарные индексы выглядят следующим образом:


Сравнивать можно также агрегатные величины, то есть величины, которые представляют собой произведение других величин. Например, индекс товарооборота характеризует изменение объема продаж, если рассчитать изменение товарооборота по одному наименованию продукции — это будет индивидуальный индекс товарооборота:
|
|
|
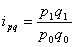 p 1 q 1 p 1 q 1
| — объем продаж в отчетном периоде; | |
| p 0 q 0 | — объем продаж в базисном периоде. | |
Общие индексы характеризуют сравнение совокупностей, групп.  = = 
| . | |
формула Ласпейреса
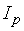 = =  ,
формула Пааше ,
формула Пааше
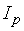 = =  . .
|
Индекс Фишера – среднегеометрическая суммы Паоше и Ласпириса 
СРЕДНИЕ ИНДЕКСЫ
 →
→ 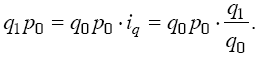 →
→  →
→ 
Индекс переменного состава Iпер представляет собой отношение двух взвешенных средних величин, характеризующее изменение индексируемого (осредняемого) показателя.
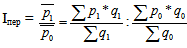
Величина этого индекса характеризует изменение средней взвешенной за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава Iфикс представляет собой отношение средних взвешенных с одним и теми же весами (т.е. при постоянной структуре).
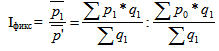
Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.
Индекс структурных сдвигов Iстр характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя.
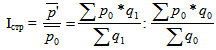
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности к общей их численности.
Система взаимосвязанных индексов при анализе динамики средних величин имеет вид:


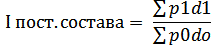

· базисные индексы: 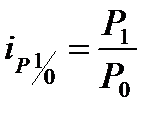 ;
;  ;
; 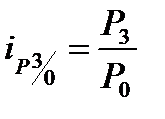 ;
;
· цепные индексы:  ;
; 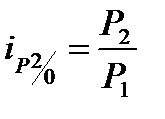 ;
; 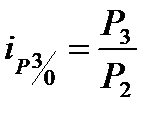 .
.
Между цепными и базисными индивидуальными индексами существует взаимосвязь, позволяющая переходить от одних индексов к другим — произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода:
 .
.
Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:
|
|
|
 ;
;  .
.
Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным и наоборот.
1. При изучении динамики цен в практике статистики применяют индексы цен в следующих формах:
- Пааше
- Ласпейреса
2. Цена товара А, производимого в организации, в базисном периоде составила 1000 р., а в текущем 1200 р. В соответствии с теорией статистики можно сказать:
· Индекс цен составил 120%
· Изменение цены отражает индивидуальный индекс цен
3. В теории статистики изменение объема реализации товара А в стоимостном выражении отражает:
· Индивидуальный индекс товарооборота
· Произведение индивидуальных индексов цены и физического объема реализации
4. Индекс структурных сдвигов, рассчитанный для рентабельности продаж, равный 1,023, показывает:
В структуре продаж увеличилась доля более рентабельных видов продукции и привела к росту средней рентабельности продаж по всем видам товаров на 2.3%
5. В социально-экономической статистике для вычисления индекса потребительских цен (индекс Ласпейреса) по формуле средней арифметической взвешенной используются следующие данные по каждой группе товаров:
- Индекс цены
- Товарооборот базисного периода
6. По данным статистики в течение года номинальная заработная плата увеличилась на 21,8%, потребительские цены за этот период увеличились на 16%. Изменение реальной зарплаты может быть выражено следующими из нижеприведенных данных:
- Возросла на 5,8%
- Возросла в 1,058 раза
7. В статистике финансов для вычисления индекса дефлятора используют следующие данные:
· Текущий объем ВВП в ценах базисного периода
· Текущий объем ВВП в текущих ценах
8. Согласно теории статистики коэффициент Лоренца характеризуют следующие утверждения:
· Изменяется от 0 до 1
· Позволяет оценить степень неравномерности распределения признака
9. В теории статистики изменение уровня себестоимости ассортимента продукции отражает:
· Сводный индекс затрат на производство
· Произведение сводных индексов себестоимости и физического объема продукции
10. В практике статистики при расчете сводного индекса Ласпейреса используют следующие данные
· Цены базисного и отчетного периода
· Количество товаров базисного периода
11. В практике статистики при расчете сводного индекса товарооборота используют следующие данные:
- Товарооборот базисного периода
- Товарооборот отчетного периода
12. По данным статистики за период 2006-2007г.г. и 2007 – 2008г.г. темпы роста цен на товары и услуги в регионе составили соответственно 110% и 107%. На основе приведенных данных можно утверждать, что темп роста цен в 2008г. по сравнению с 2006г:
|
|
|
- Равен 117,7%
- Характеризует повышение цен на 17,7%
|
|
|


