 |
Одностороннее действие нагрузки (отнулевой цикл)
|
|
|
|
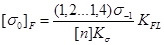, (3.12)
где [n] – требуемыйкоэффициент запаса прочности, [n]= 1,4…2,2; КFL – коэффициент долговечности при изгибе; Кσ – эффективный коэффициент концентрации напряжений у ножки зуба, Кσ = 1,4…1,6; σ-1 – предел выносливости сталей: для углеродистых сталей σ-1 ≈ 0,43 σВ МПа; для легированных сталей σ-1≈ 0,35 σВ + (70…120) МПа.
3.2.4. Переменное направление нагрузки
(симметричный знакопеременный цикл)
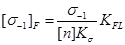(3.13)
3.3. Определение коэффициента нагрузки
и степени точности передачи
Во все зависимости для определения основных параметров зацепления и напряжений, возникающих при работе передачи, входит не номинальная, а расчетная нагрузка.
Мрасч =Мн К = Мн Кдин Ккц, (3.14)
где К – коэффициент нагрузки; Кдин – коэффициент динамичности, зависит от величины окружной скорости и точности изготовления; Ккц – коэффициент концентрации нагрузки, учитывает неравномерность распределения нагрузки по длине зуба за счет деформации валов и колес.
При выполнении проектного расчета, когда параметры передачи и окружная скорость еще неизвестны, принимают: при симметричном расположении колес относительно опор К= Кдин Ккц = 1,3; при несимметричном или консольном расположении К= Кдин Ккц = 1,5.
После определения размеров передачи значение коэффициента нагрузки уточняют по фактическим данным.
3.4. Назначение коэффициента ширины зуба ψа
Стандарт (ГОСТ 2185-88) устанавливает следующие значения ширины зуба (ψа= в/аw):
Таблица 10
| Прямозубые | Косозубые | Шевронные |
| 0,16; 0,2; 0,25; 0,315; 0,4 | 0,315; 0,4; 0,5; 0,63 | 0,5; 0,63; 0,8; 1,0; 1,25 |
| Рекомендации: 1. Меньшие значения каждого диапазона рекомендуется применять для коробок передач, а большие – для редукторов; 2. При консольном расположении колес значение ψа следует принимать меньше; 3. Для тихоходной ступени значение ψа следует принимать большим, чем для быстроходной; 4. Увеличение точности изготовления и монтажа позволяет увеличить значение ψа. |
Ширина колеса (венец) b2 = aw ψа; ширина шестерни назначается больше – b2 = aw ψа + (4…5) мм.
|
|
|
Определение межосевого расстояния зубчатой передачи и модуля зацепления
Межосевое расстояние цилиндрической зубчатой передачи определяют по зависимости:
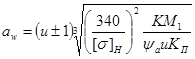, мм (3.15)
где [σ]H – допускаемое контактное напряжение в МПа; М1 – номинальный крутящий момент на шестерне в Нмм; U – передаточное число; КП – коэффициент, учитывающий влияние суммарной длины контактных линий на повышение нагрузочной способности передачи, для пряпозубых колес КП =1,0; для косозубых колес: при твердости НВ ≤ 350 и β < 250 КП = 1,35…1,5 (меньшие значения при Z ≤ 20, а большие – при Z1 > 40); при твердости HB > 350, а также при β > 250 независимо от твердости КП = 1,15.
Полученное значение аw округляют до ближайшего стандартного значения по ГОСТ 2185-88 (табл.11).
Таблица 11
Стандартные значения межосевого расстояния, мм
| 1 ряд | 40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 580 |
| 2 ряд | 71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710 |
Модуль зацепления ориентировочно принимают по зависимости:
m = (0,01…0,02)aw, мм. (3.16)
Полученное значение модуля округляем до ближайшего стандартного значения по ГОСТ 9563 – 88 (табл. 12).
Таблица 12
Стандартные значения модуля, мм
| 1 ряд | 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 |
| 2 ряд | 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11 |
Расчет чисел зубьев, фактического передаточного числа и угла наклона зуба
Определение числа зубьев
Суммарное число зубьев Zc для прямозубых колес:
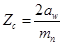(3.17)
для косозубых и шевронных колес:
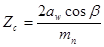(3.18)
Угол наклона зуба β принимают:
Для косозубых колес β= 80…150; для шевронных колес β = 250…400.
Числа зубьев шестерни и колеса:
|
|
|
Z1= (Zc)/(u+1); Z2 = Zc – Z1 (3.19)
Полученные значения чисел зубьев округляют до целых чисел. Рекомендуется для шестерен быстроходных ступеней принимать Z1 = 20…30, а для последующих ступеней Z1 = 17…24.
Уточнение фактического передаточного числа.
Uф = Z2/Z1 (3.20)
Отклонение фактического передаточного числа от проектного (заданного) не должно превышать 3,5%.
Проверка условия сборки
Для прямозубых колес:
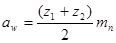, мм, (3.21)
Если для прямозубых колес не удовлетворяется условие сборки, то передачу необходимо вписать в стандартное межосевое расстояние за счет коррегирования.
Для косозубых колес уточняют фактический угол наклона зуба:
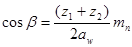, (3.22)
При этом угол наклона зуба не подлежит изменению и стандартизации, например β = 13015’
Затем назначают степень точности передачи (табл. 13), ориентируясь на окружную скорость:
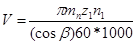, м/с (3.23)
Таблица 13
Рекомендуемая степень точности изготовления
зубчатых передач
| Степень точности | Окружная скорость, м/с | |
| прямозубые | непрямозубые | |
| 8 (пониженная) | до 8 | до 12 |
| 7 (нормальная) | до 12 | до 20 |
| 6 (повышенная) | до 20 | до 31,5 |
|
|
|
