Проверка действительных контактных напряжений

Проверка действительных контактных напряжений выполняется после уточнения величины коэффициента нагрузки и определения геометрических размеров зубчатых колес по зависимости:

, МПа (3.24)

где К – уточненное значение коэффициента нагрузки; U – фактическое передаточное число.

Затем необходимо рассчитать отклонение действительного контактного напряжения σ_Н и [σ]_Н, отклонение не должно превышать +5…- 20%. При перегрузке необходимо увеличить межосевое расстояние до ближайшего большего из стандартного ряда.

Проверка прочности зубьев шестерни и колеса на изгиб

Проверка изгибных напряжений производится по формуле:

, МПа (3.25)

где Р – окружное усилие, Н; Y – коэффициент формы зуба, определяется в зависимости от числа зубьев: действительного для прямозубых колес и эквивалентного (Z_v) для косозубых и шевронных колес (Z_v= Z/ cos³β), см табл. 14; К_П – коэффициент повышения нагрузочной способности на изгиб косозубых и шевронных колес (его значения такие же, как и для расчета на контактную прочность): m_n - нормальный модуль (стандартный модуль), мм.

В зависимости от Z_v по табл. 14 находят Y и на изгиб рассчитывают зубья того из пары сцепляющихся колес, для которого произведение Y[σ]_F меньше.

 

Таблица 14

Коэффициент формы зуба Y

Число зубьев Z	Зубчатые колеса внешнего зацепления при коэффициенте смещения исходного контура	Зубчатые колеса с внутренними зубьями
-0,2		+0,2
	0,239	0,308	0,378	-
	0,266	0,330	0,392	-
	0,302	0,355	0,408	-
	0,330	0,377	0,424	-
	0,348	0,389	0,431	-
	0,367	0,402	0,437	-
	0,384	0,414	0,445	-
	0,400	0,426	0,455	-
	0,408	0,434	0,458	0,942
	0,416	0,440	0,464	0,916
	0,431	0,452	0,473	0,863
	0,445	0,465	0,485	0,825
	0,452	0,471	0,490	0,795
	0,459	0,477	0,495	0,769
	0,474	0,490	0,507	0,731
	0,485	0,449	0,512	0,688
	0,494	0,505	0,517	0,660
	0,508	0,515	0,523	0,620
Рейка	-	0,550	-	-

Усилия, действующие в цилиндрическом косозубом зацеплении

Окружное усилие:

P = 2M₁/d₁, d₁ = m_nZ₁ (3.26)

Радиальное усилие:

R = P tgα/cosβ, (3.27)

где α – угол зацепления, α – угол зацепления, α = 20⁰

Осевое усилие:

Q = Ptgβ. (3.28)

4. Последовательность расчета
конических передач

Определение диаметра колеса

 

Допускаемые контактные напряжения определяют также, как для цилиндрических колес.

При расчете конической передачи коэффициент нагрузки принимают равным К = 1,5 из-за консольного расположения конической шестерни.

Требуемый внешний делительный диаметр колеса из условия контактной прочности равен:

, мм (4.1)

где М₁ – крутящий момент на валу шестерни, Н´мм; [σ]_H – допускаемое контактное напряжение, Н/ мм²; Ψ_Re – коэффициент ширины венца (при проектном расчете Ψ_Re ≤ 0,3); К_П – коэффициент нагрузочной способности конических колес, для прямозубых колес К_П = 0,85, для косозубых колес К_П = 1,2…1,3.

Полученное значение d_e2 округляем до стандартного значения из ряда: 50; (56); 63; (71);80; 90; 100; (112); 125; (140); 160; (180); 200; (225); 250; 280; 315; 335; 400…

Определение числа зубьев шестерни и колеса

Число зубьев шестерни обычно назначают в пределах: Z₁= 18… 20. Более точно число зубьев можно определить по данным табл. 15. Число зубьев колеса: Z₂ =Z₁ ´ U

Таблица 15

Рекомендуемое минимальное число зубьев шестерни

U	Z1 при β
0 – 150	20 – 250	30 – 400
> 3,15

Определение внешнего (окружного) модуля передачи и фактического передаточного числа

Внешний окружной модуль конической передачи равен:

, мм (4.2)

Полученное значение модуля m_te необходимо округлить до ближайшего стандартного значения (табл. 15).

Уточняют фактическое передаточное число:

Z₂ =d_e2/m_te, Z₁ =Z₂/U, U_ф= Z₂/Z₁.

Отклонение полученного фактического передаточного числа от стандартного допускается в пределах ± 3%.

4.4. Определение внешнего конусного расстояния
и угла наклона зуба

Внешнее конусное расстояние (по принятому модулю m_te):

, мм. (4.3)

Ширина венца b = ψ_Re´R_e, мм

Уточняют угол β_m (средний угол наклона зуба на делительном конусе). Для этого сначала определяют β_e – наружный угол наклона зуба на делительном конусе по соотношению:

, (4.4)

Определение углов делительных конусов и среднего окружного модуля

 

Углы делительных конусов:

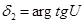, , δ₁ + δ₂ = 90⁰ (4.5)

Средний окружной модуль m_tm:

, мм. (4.6)

Средний нормальный модуль m_nm:

, мм. (4.7)

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: