 |
Геометрическая вероятность.
|
|
|
|
Задача 7.
Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости или пространства).
Обозначим меру (длину, площадь, объем) области через m(Ω). При этом вероятность попадания точки, брошенной наудачу в область A - часть области Ω, равна отношению мер областей A и Ω, соответственно равные m(A) и m(Ω).
Формула геометрической вероятности 
имеет вид: 
.
Решение задач.
Задача о встрече
Пьеро и Буратино условились встретиться в определенном месте между двумя и тремя часами дня. Они договорись, что тот, кто придет первым, ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность их встречи , если каждый из друзей может прийти в любое время в течение указанного часа независимо от другого?
Решение. Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть х и у — моменты прихода Пьеро и Буратино (они являются точками отрезка [0,1]). Все возможные результаты эксперимента – множество точек квадрата со стороной 1: 
.
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества 
(10 минут = 1/6 часа). То есть попадание в множество А наудачу брошенной в квадрат точки означает, что Буратино и Пьеро встретятся. Тогда вероятность встречи равна 
.
2. В прямоугольник 5*4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
Решение: По определению геометрической вероятности искомая вероятность равна отношению площади круга (в который точка должна попасть) к площади прямоугольника (в которой точка ставится), т.е.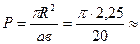 
0353.
|
|
|
3. В треугольник с вершинами в точках (−1,0); (0, 1); (3,0) наудачу брошена точка (х, у). Найти вероятность того, что координаты точки удовлетворяют неравенству
2x + y ≤ 0.
Решение: Сделать чертеж. Закрасить область, удовлетворяющую условию задачи.P=1/6.
Тема 4
Полная вероятность. Формула Байеса.
Задача 8.
Пусть событие А может произойти в результате осуществления одного события из
некоторой полной группы событий H1, H2, …Hn.
События этой группы обычно называют гипотезами. Тогда
P(A) = P(H1)PH1(A) + P(H2) PH2(А) +…+ P(Hn)PHn(A) (1)
(формула полной вероятности), причем
P(H1) +P(H2) +…+ P(Hn) = 1.
Пусть в результате испытания произошло событие А, которое могло наступить только
вместе с одним из событий H1, H2,…Hn, образующих полную группу событий (они
называются гипотезами). Требуется найти вероятность событий H1, H2,… Hn после
испытания, когда событие А имело место, т.е. PA(Hi), i = 1,2,…n. Для нахождения этих вероятностей используют формулы Байеса (формулы гипотез):
PA (Hi) = 
(2)
Замечания.
1) Вероятности PA(H1) называются послеопытными (апостериорными) вероятностями
гипотез Hi, а вероятности P(Hi) - доопытными (априорными) вероятностями гипотез
Hi. Эти вероятности различаются.
2) Знаменатель в правой части формулы (2) совпадает с правой частью формулы (1) и
равен P(A).
Решение задач.
1. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: Нi – взятая наудачу деталь обработана на i-ом станке,i=1,2,3.
|
|
|
Условные вероятности (в условии задачи они даны в форме процентов):
, 
, 
.
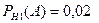Зависимости между производительностями станков означают следующее: 
. Причем P(H1) +P(H2) +P(H3) = 1,так как гипотезы образуют полную группу.
Для того, чтобы найти вероятности появления гипотез, нам придется решить систему вышеперечисленных уравнений. Решив ее, получим 
.
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
P(A) = P(H1)PH1(A) + P(H2) PH2(А) + P(H3)PH3(A)== 
.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
,
,
.
Таким образом, доли деталей каждого станка среди бракованных деталей на конвейере для первого станка составляет 33%, второго – 39%, третьего – 28%.
Тема 5
Повторные испытания.
Задачи 9-11.
Формула Бернулли: Если производится n независимых испытаний, в каждом из которых событие А появится с вероятностью р, то вероятность того, что событие А появится ровно k раз в n испытаниях, выражается формулой, которую называют формулой Бернулли
Pn(k) = Cnkpk qn – k ,где q=1-p (1),
Иногда бывают полезны следующие формулы: Вероятность того, что событие A:
1) наступит n раз: 
; (2)
2) не наступит ни разу: 
; (3)
3) наступит хотя бы один раз: 
; (4)
4) наступит не более k раз: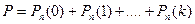 
(5)
или 
. (6)
5) наступит не менее k раз: 
(7)
или 
. (8)
Из формул (5)и(6), а также (7)и (8) выбирают ту, которая содержит меньше слагаемых.
|
|
|
