 |
Наивероятнейшее число наступлений события
|
|
|
|
Наивероятнейшее число m0 определяется из двойного неравенства
np - q 
m0 np + p (9)
Формула Пуассона (лучше использовать при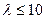 
.)
Теорема: Если вероятность p наступления события А в каждом испытании постоянна и близка к нулю (р 
), а число независимых испытаний n достаточно велико (
), причем произведение np стремится к постоянному числу 
то вероятность Pn(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна: 
(11)
Локальная теорема Муавра-Лапласа (рекомендуется применять при npq 
).
Пусть в серии из n независимых испытаний вероятность наступления события А в каждом испытании равна р (0<p<1), q=1-p, 
. Если 
и величина 
является ограниченной, тогда 
(12).
Таблица значений функции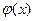 
приведена в приложении. Функция 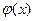является четной, т.е 
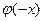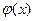= , монотонно убывающей при х>4 практически 
.
Интегральная теорема Муавра-Лапласа (удобно применять при npq ).
Если n – велико, а р – отлично от 0 и 1, то 
где 
- функция Лапласа. Таблица значений функции 
приведена в приложении. Функция является нечетной, т.е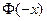 
=- .Если х>4, то 
в силу монотонного возрастания функции .
Решение задач:
Полагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятности следующих событий:
1) а) при 12 выстрелах мишень будет поражена 7 раз;
б) при 12 выстрелах мишень будет поражена менее 4 раз;
в) при 12 выстрелах мишень будет поражена не более 8 раз;
2) Наивероятнейшее число выстрелов, которые поразят мишень при 125 сделанных выстрелах. И вероятность этого числа попаданий.
3) При 200 выстрелах мишень будет поражена не менее 110, но не более 130 раз.
4) При 200 выстрелах мишень будет поражена не более 110 раз;
5) При 200 выстрелах мишень будет поражена не менее 115 раз.
|
|
|
6) На стрельбы пришла Полина Александровна. Для нее вероятность попадания в мишень равна 0,04. Найти вероятность того, что из 200 выстрелов Полина Александровна попадет в мишень 10 раз.
Решение:
1) воспользуемся формулами Бернулли:
а) Р12(7)= 
;
б) при 12 выстрелах мишень будет поражена менее 4 раз означает, что мишень будет поражена 0, 1, 2 или 3 раза. Ищем Р12(0)+Р12(1)+Р12(2)+Р12(3)= 
+ 
+ 
+ 
0,000017+0,000302+0,002491+0,012457=0,12738.
в) при 12 выстрелах мишень поражена не более 8 раз означает, что она поражена 0,1,2,…,8 раз. Вычисление каждой из этих вероятностей и их последующее суммирование приведет к очень громоздким вычислениям. Противоположным событием будет событие, состоящее в том, что мишень поражена более 8 раз, т.е. 9, 10, 11 или 12.
Найдем Р12(9)+Р12(10)+Р12(11)+Р12(12)= 
+ 
0,14189+0,06385+0,01741+
+0,002177=0,225331. Нас интересует вероятность противоположного события, т.е. искомая вероятность равна 1- (Р12(9)+Р12(10)+Р12(11)+Р12(12)) 
.
2) Наивероятнейшее число выстрелов, которые поразят мишень при 125 сделанных выстрелах. Воспользуемся формулой: np - q m0 np + p. Подставив в формулу n=125, р=0,6, q=0,4, получим 74,6 m0 75,6. Следовательно, наивероятнейшее число попаданий будет равно 75.
Найдем 
Т.к. n=200 достаточно велико (условие 
), применяем локальную теорему Муавра-Лапласа. Сначала определим 
.Тогда по формуле 
.
Значение 
найдено по табл.1 приложений.
3) Найдем вероятность того, что при 200 выстрелах мишень будет поражена не менее 110, но не более 130 раз. Так как количество выстрелов и количество попаданий достаточно велико, применение формулы Бернулли будет связано с большими трудностями. Применим интегральную формулу Муавра-Лапласа. Здесь n=200, р=0,6,q=0,4, k1=110, k2=130.
.
Теперь по формуле (15) и учитывая свойства Ф(х), получим
Р200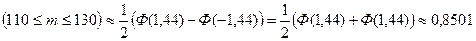 
(по таблице 2 приложений, Ф(1,44) 
).
4) При 200 выстрелах мишень будет поражена не более 110 раз. Ищем Р200 
.. Применим интегральную формулу Муавра-Лапласа. Здесь n=200, р=0,6,q=0,4, k1=0, k2=110.
.
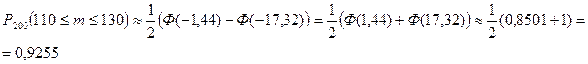
5) Вероятность того, что при 200 выстрелах мишень будет поражена не менее 115 раз будем искать, также применяя интегральную формулу Муавра-Лапласа.
|
|
|
Задачи в классе. Здесь n=200, р=0,6,q=0,4, k1=115, k2=200.
.
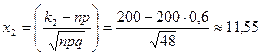6) На стрельбы пришла Полина Александровна. Для нее вероятность попадания в мишень равна 0,04. Найти вероятность того, что из 200 выстрелов Полина Александровна попадет в мишень 10 раз.
р=0,04, q=0,96, n=200, m=10.
Т.к. n=200 достаточно велико (условие 
), применяем теорему Пуассона , где 
. 
. Значение Р10(8) берем из таблицы в приложении III.
Тема 6.
|
|
|
