 |
Дискретные случайные величины.
|
|
|
|
Задачи 12-13.
Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.
Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей изучала главным образом случайные события, то современная теория вероятностей преимущественно имеет дело со случайными величинами.
Сами случайные величины обозначаются прописными латинскими буквами X, Y, Z и т.д., а их возможные значения – соответствующими строчными x, y, z. Например, если случайная величина имеет три возможных значения, то будем обозначать их так: х1,х2,х3.
Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной (дискретно распределенной).
Соответствие между возможными значениями случайной величины и их вероятностями называют законом распределения дискретной случайной величины.
Закон распределения можно задать в виде таблицы, формулы или графически.
При табличном задании закона распределения в первой строке таблицы перечислены все значения случайной величины в порядке возрастания, а в нижней – соответствующие им вероятности.
| Х | х1 | х2 | х3 | ….. | xn |
| Р | p1 | p2 | p3 | ….. | pn |
Причем следует учитывать, что
(1).
Для наглядности ряд распределения случайной величины можно изобразить графически. Для этого в прямоугольной системе координат по оси абсцисс ОХ будем откладывать значения случайной величины, k=1, 2, …, n, а по оси ординат OY – соответствующие им вероятности р1, р2, …, рn. Полученные точки соединяются отрезками прямых.
Построенная таким образом фигура называется многоугольником или полигоном распределения вероятностей.
|
|
|
Многоугольник распределения, также как и ряд распределения, полностью характеризует случайную величину. Он является одним из форм закона распределения.
Функция распределения дискретной случайной величины.
Наиболее общей формой закона распределения является функция распределения, представляющая собой вероятность того, что случайная величина Х примет значение меньшее, чем заданное х.
F(х)=Р{X<x} (2).
ФункциюF(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х.
Дан ряд распределения случайной величины Х.
| xi | ||||
| pi | 0,4 | 0,3 | 0,1 | * |
Найти значение *, найти и изобразить графически функцию распределения.
Решение: так как сумма всех вероятностей, стоящих в нижней строке есть величина равная 1, *=1-(0,4+0,3+0,1)=0,2. Т.е. вероятность того, что случайная величина Х примет значение 7, равна 0,2.
Для нахождения функции распределения б удем задавать различные значения х и находить для них F(х)=Р{X<x}.
1. Если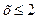 
, то, очевидно, F(x)=0 в том числе и при х=2 F(2)=P(X<2)=0.
2. Если 
, например, х=3; F(x)=P(X=2)=0,4. очевидно, что и F(4)=P(X<4)=0,4.
3. Если 
, например, х=5; F(x)=P(X=2)+P(X=4)=0,4+0,3=0,7. очевидно, что и F(6)=P(X<6)=0,7.
4. Если 
, например, х=6,123; F(x)=P(X=2)+P(X=4)+P(X=6)=0,4+0,3+0,1=0,8. очевидно, что и F(7)=P(X<7)=0,8.
5. Если 
, например, х=8; F(x)=P(X=2)+ P(X=4)+P(X=6)+P(X=7)==0,8+0,2=1.
|
| . 
|
Заметим, что при подходе слева к точкам разрыва функция сохраняет свое значение, иначе говоря, функция распределения непрерывна слева.
Итак, функция распределения дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующим возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции равна 1.
|
|
|
|
|
|
