 |
Интегральное исчисление функций одной переменной
|
|
|
|
Филиал федерального государственного бюджетного образовательного учреждения высшего образования «Мурманский арктический государственный университет»
В г. Апатиты
МАТЕМАТИКА
Методическое пособие для студентов
(заочное отделение)
специальности
071600 «Высоковольтные энергетика и электротехника»
180400 «Электропривод и автоматика промышленных
установок и технологических комплексов»
«Технофизика»
Составитель:
преподаватель кафедры общих дисциплин, доцент,
к.ф.-м.н Дашкевич Ж.В...
Семестр
Математический анализ
Программа курса
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Числовые последовательности.
1. Числовые последовательности и операции над ними, ограниченные и неограниченные последовательности.
2. Бесконечно большие и бесконечно малые последовательности, основные свойства бесконечно малых последовательностей.
3. Сходящиеся последовательности: предел последовательности, основные свойства сходящихся последовательностей.
4. Монотонные последовательности, число е.
Функции
5. Определение функции. Способы задания функций.
6. Предел функции. Односторонние пределы. Свойства пределов. Два замечательных предела.
7. Непрерывность и разрывы функции.
8. Классификация элементарных функций.
9. Обратные функции.
10. Сложные функции.
Дифференцирование
11. Определение производной. Ее геометрический и физический смысл.
12. Правила дифференцирования.
13. Производные от элементарных функций. Таблица производных.
14. Дифференциал: определение и геометрический смысл, правила вычисления.
15. Дифференцирование функции, заданной параметрически.
|
|
|
16. Производные высших порядков.
Применение дифференциального исчисления к исследованию функций
17. Раскрытие неопределенностей. Правило Лопиталя.
18. Формулы Тейлора и Маклорена.
19. Разложение в ряд Маклорена элементарных функций, вычисление числа е.
Исследование графика функции
20. Участки монотонности и отыскание точек экстремума функций (необходимое и достаточное условия).
21. Направление выпуклости и точки перегиба графика функции.
22. Асимптоты графика функции.
Рекомендуемая литература
В.А.Ильин, Э.Г.Позняк, Основы математического анализа, М., Наука, Вып. 1 (1967 г), Вып 2 (1980 г.),
В.М.Шипачев, Высшая математика, М., Высшая школа, 1998.
Данко П.Е., Попов А.Г., Кожевникова В.М., Высшая математика в упражнениях и задачах, ч.1,ч.2, М., Высшая школа, 1998.
В.М.Шипачев, Задачник по высшей математике, М., Высшая школа, 1998.
В.П.Минорский, Сборник задач по высшей математике, М., Наука, 1971.
КОНТРОЛЬНОЕ ЗАДАНИЕ
(номер варианта определяется по последнему номеру зачетной книжки)
Вариант № 1
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя
 |
3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

Вариант № 2
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

Вариант № 3
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции
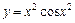
4. Исследовать функцию и построить ее график

Вариант № 4
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

Вариант № 5
1. Вычислить предел функции
|
|
|

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график
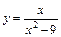
Вариант № 6
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

5. Найти все частные производные функции
Вариант № 7
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

5. Найти все частные производные функции

Вариант № 8
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производн 
ые функций
 и
и 
4. Исследовать функцию и построить ее график

Вариант № 9
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

Вариант № 10
1. Вычислить предел функции

2. Вычислить предел функции, используя правило Лопиталя

3. Вычислить производную 
функции

4. Исследовать функцию и построить ее график

Семестр
Математический анализ
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Неопределенный интеграл.
Понятие первообразной функции и неопределенного интеграла.
Основные свойства неопределенного интеграла.
Основные методы интегрирования.
Определенный интеграл.
Определенный интеграл: интегральные суммы, определение и основные свойства.
Формула Ньютона – Лейбница для вычисления определенных интегралов.
Методы вычисления определенных интегралов: замена переменной под знаком интеграла, интегрирование по частям.
Приложения определенного интеграла.
Вычисление с помощью определенного интеграла длины дуги кривой.
Вычисление с помощью определенного интеграла площади плоской фигуры.
Вычисление с помощью определенного интеграла объема тела вращения.
Несобственные интегралы.
Несобственные интегралы 1 рода: определение, понятие сходимости.
Несобственные интегралы 2 рода: определение, понятие сходимости.
|
|
|
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ.
Кратные интегралы.
|
|
|


