 |
Определение и основные свойства кратного интеграла Римана. Сведение двойных и тройных интегралов к повторным. Замена переменных в кратном интеграле.
|
|
|
|
Криволинейные интегралы.
Криволинейные интегралы 1-го рода и их свойства, сведение криволинейных интегралов 1-го рода к определенным интегралам. Криволинейные интегралы 2-го рода и их свойства, сведение криволинейных интегралов 2-го рода к определенным интегралам. Формула Грина на плоскости, применение формулы Грина к вычислению площадей.
Поверхностные интегралы.
Простые поверхности. Криволинейные координаты на поверхности. Формулы площади простой поверхности при различных способах ее задания. Поверхностные интегралы 1-го и 2-го рода.
Теория поля.
Скалярные и векторные поля. Производная скалярного поля по направлению, градиент, оператор Гамильтона. Дивергенция и ротор векторного поля в декартовых координатах. Формула Остроградского-Гаусса. Формула Стокса. Инвариантность divA и rotA. Потенциальные и соленоидальные векторные поля.
Рекомендуемая литература
В.А.Ильин, Э.Г.Позняк, Основы математического анализа, М., Наука, Вып. 1 (1967 г), Вып 2 (1980 г.),
Г.М.Фихтенгольц, Основы математического анализа, М., Наука, 1968.
В.М.Шипачев, Высшая математика, М., Высшая школа, 1998.
Б.П.Демидович, Сборник задач и упражнений по математическому анализу, М., Наука, 1969.
Данко П.Е., Попов А.Г., Кожевникова В.М., Высшая математика в упражнениях и задачах, ч.1,ч.2, М., Высшая школа, 1998.
В.М.Шипачев, Задачник по высшей математике, М., Высшая школа, 1998.
В.П.Минорский, Сборник задач по высшей математике, М., Наука, 1971.
КОНТРОЛЬНОЕ ЗАДАНИЕ №1
Вариант № 1
5. Вычислить методом подстановки
6. Вычислить методом интегрирования по частям
7. Вычислить интеграл от рациональной функции
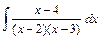
8. Вычислить площадь фигуры, ограниченной линиями
|
|
|
и 
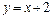
Вариант № 2
1. Вычислить методом подстановки
2. Вычислить методом интегрирования по частям
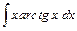
3. Вычислить интеграл от рациональной функции
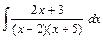
4. Вычислить площадь фигуры, ограниченной линиями
и 
Вариант № 3
- Вычислить методом подстановки
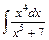
- Вычислить методом интегрирования по частям
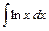
- Вычислить интеграл от рациональной функции
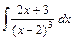
- Вычислить площадь фигуры, ограниченной линиям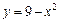и
и 
Вариант № 4
- Вычислить методом подстановки
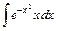
- Вычислить методом интегрирования по частям
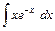
- Вычислить интеграл от рациональной функции
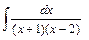
- Вычислить площадь фигуры, ограниченной линиями
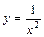, x = 1 и x = 2
Вариант № 5
- Вычислить методом подстановки
- Вычислить методом интегрирования по частям
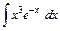
- Вычислить интеграл от рациональной функции
- Вычислить площадь фигуры, ограниченной линиями
, y = x, x = 0, x = 1.
Вариант № 6
- Вычислить методом подстановки
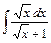
- Вычислить методом интегрирования по частям
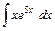
- Вычислить интеграл от рациональной функции
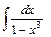
- Вычислить площадь фигуры, расположенной в 1 четверти и ограниченной линиям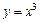и
и 
Вариант № 7
- Вычислить методом подстановки
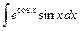
- Вычислить методом интегрирования по частям
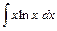
- Вычислить
интеграл от рациональной функции
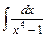
- Вычислить площадь фигуры, ограниченной линиям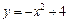и
и 
Вариант № 8
- Вычислить методом подстановки
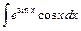
- Вычислить методом интегрирования по частям
- Вычислить интеграл от рациональной функции
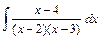
- Вычислить площадь фигуры, ограниченной линиями
и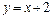
Вариант № 9
- Вычислить методом подстановки
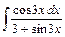
- Вычислить методом интегрирования по частям
- Вычислить интеграл от рациональной функции
- Вычислить площадь фигуры, ограниченной линиям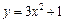и
и 
Вариант № 10
- Вычислить методом подстановки
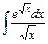
- Вычислить методом интегрирования по частям
- Вычислить интеграл от рациональной функции
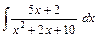
- Вычислить площадь фигуры, ограниченной линиям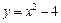и
и 
|
|
|
Семестр
Линейная алгебра и аналитическая геометрия
Основы линейной алгебры
1. Матрицы. Типы матриц.
2. Операции над матрицами.
3. Определители. Вычисление определителей 2-го и 3-го порядка.
4. Миноры и алгебраические дополнения, теорема Лапласа.
5. Свойства определителей.
6. Обратная матрица, существование и вычисление.
|
|
|
