 |
Проверка статистических гипотез.
|
|
|
|
28. Статистические гипотезы. Виды гипотез.
29. Статистический критерий. Критическая область.
30. Уровень значимости и мощность критерия.
31. Критерий Пирсона.
Регрессия и корреляция между случайными величинами.
32. Статистическая, корреляционная зависимости, регрессия.
33. Корреляционная таблица.
34. Эмпирическая линия регрессии.
35. Прямая среднеквадратической регрессии, коэффициент регрессии.
36. Выборочный коэффициент корреляции, его свойства.
Рекомендуемая литература
Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высш. Шк., 1999.—479 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. Шк., 1999.—400 с.
Печинкин А.В., Тескин О.И., Цветкова Г.М. Теория вероятностей. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999.— 456 с.
Горяинов В.Б., Павлов И.В., Цветкова Г.М. Математическая статистика. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.—424 с.
Контрольное задание
Вариант №1
1. За круглым столом случайным образом сидят 6 человек, среди которых A и B. Какова вероятность того, что A и B окажутся рядом?
2. В отделе имеется два компьютера. Вероятность исправной работы в течении года для первого компьютера равна 0,8, а для второго – 0,85. Случайная величина X – число компьютеров, не потребовавших ремонта в течении года. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости веса Y (в кг) цилиндрических болванок от их длины X (в см):
Значения X:
Соответствующие значения Y:
|
|
|
| 1.16 | 1.21 | 1.24 | 1.23 | 1.16 | 1.19 | 1.18 | 1.18 | 1.16 | 1.22 | 1.23 | 1.21 | 1.17 | 1.23 | 1.16 | 1.23 | 1.21 |
| 1.23 | 1.18 | 1.22 | 1.17 | 1.16 | 1.20 | 1.22 | 1.25 | 1.17 | 1.22 | 1.20 | 1.19 | 1.21 | 1.22 | 1.25 | 1.16 | 1.20 |
| 1.18 | 1.25 | 1.18 | 1.24 | 1.21 | 1.25 | 1.20 | 1.20 | 1.22 | 1.23 | 1.20 | 1.19 | 1.17 | 1.20 | 1.20 | 1.17 |
4.
Вариант №2
1. На двух карточках написана буква А, на трех – буква В и на четырех – буква З. Последовательно вынимаются и кладутся слева направо 4 карточки. Какова вероятность того, что получится слово ВАЗА?
2. Вероятность того, что телефон справочной службы окажется не занят равна 0,4. Абонент хочет дозвониться до справочной, для чего предпримет не более четырех попыток. Случайная величина X – число использованных попыток. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. В результате исследования зависимости мощности 50 двигателей Y (в квт) от числа оборотов X (в сотнях об/мин) получены следующие результаты:
Значения X:
Соответствующие значения Y:
| 25.9 | 26.9 | 27.8 | 27.1 | 25.9 | 27.2 | 27.9 | 27.6 | 25.9 | 27.8 | 27.1 | 27.3 | 26.9 | 26.6 | 28.7 | 27.7 | 27.6 |
| 26.0 | 28.0 | 27.1 | 26.7 | 26.6 | 27.6 | 26.3 | 26.9 | 27.0 | 27.9 | 27.1 | 27.1 | 26.9 | 27.1 | 28.7 | 26.4 | 25.9 |
| 28.7 | 26.8 | 28.2 | 27.1 | 28.1 | 27.8 | 26.5 | 28.6 | 27.1 | 27.5 | 27.5 | 27.2 | 28.6 | 27.1 | 26.7 | 26.7 |
Вариант №3
1. Номер автомобиля содержит 4 цифры. Какова вероятность того, что первые две цифры окажутся равными двум последним (например, 1313)?
2. На склад поступило семь принтеров, из них – 4 новых и 3 бывших в употреблении. Случайная величина X – число новых принтеров из двух наудачу выбранных. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
|
|
|
3. В результате экспериментального исследования зависимости температуры воздуха в кабине трактора Y (в градусах) от температуры наружного воздуха X (в градусах) получены следующие результаты:
Значения X:
Соответствующие значения Y:
| 27.03 | 36.20 | 36.03 | 33.22 | 27.03 | 38.88 | 31.29 | 34.44 | 27.03 | 35.06 | 33.64 | 36.88 | 32.42 | 32.46 | 39.56 | 34.21 | 39.10 |
| 34.84 | 34.94 | 34.69 | 38.04 | 30.44 | 38.58 | 36.64 | 32.54 | 39.20 | 31.63 | 36.36 | 40.77 | 30.92 | 37.78 | 44.65 | 44.65 | 36.41 |
| 41.45 | 44.65 | 38.21 | 36.88 | 38.85 | 44.65 | 35.10 | 35.00 | 28.25 | 36.42 | 39.96 | 34.76 | 32.18 | 33.22 | 30.93 | 40.99 |
Вариант №4
1. Три завода выпускают одинаковые изделия. Вероятность изделию первого завода оказаться бракованным равна 0,3, изделию второго завода – 0,2, третьего завода – 0,1. Взято по одному изделию каждого завода. Какова вероятность того, что среди них окажутся не менее двух бракованных?
2. Вероятность того, что покупатель обнаружит в магазине нужную ему вещь равна 0,85. В микрорайоне три магазина, которые покупатель обходит последовательно в поисках этой вещи пока ее не обнаружит либо не обойдет все магазины. Случайная величина X – число магазинов, которые обойдет покупатель. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости годового расхода топлива на один трактор Y (в тоннах) от годовой выработки трактора X (в сотнях га):
Значения X:
| 6.8 | 6.1 | 7.8 | 4.8 | 6.9 | 8.8 | 3.8 | 7.5 | 7.4 | 9.8 | 6.1 | 3.4 | 9.4 | 8.1 | 6.6 | 8.0 | 7.9 |
| 4.7 | 10.1 | 9.5 | 8.2 | 3.4 | 5.4 | 6.6 | 6.2 | 3.9 | 8.1 | 8.7 | 4.0 | 5.2 | 9.6 | 10.8 | 8.2 | 9.2 |
| 7.7 | 5.7 | 9.0 | 10.3 | 8.5 | 6.2 | 5.4 | 5.9 | 5.6 | 4.9 | 11.0 | 5.3 | 8.4 | 7.7 | 8.5 | 6.2 |
Соответствующие значения Y:
Вариант №5
1. К Новому году пяти детям были приготовлены пять различных подарков. Однако Дед Мороз перепутал подарки и вручил их детям случайным образом. Какова вероятность того, что каждый ребенок получил свой подарок?
|
|
|
2. Вероятность того, что саженец приживется равна 0,8. Было куплено четыре саженца. Случайная величина X – число прижившихся саженцев. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости отклонений размеров валиков от номинала при чистовой обработке Y (в мкм) от отклонений размеров валиков от номинала при черновой обработке X (в мкм):
Значения X:
| -5 | -21 | -12 | -12 | -14 | -16 | -19 | -11 | -10 | -28 | -11 | -15 | -14 | -16 | -16 | ||
| -17 | -24 | -1 | -5 | -2 | -8 | -20 | -12 | -3 | -9 | -12 | -29 | -10 | -2 | -13 | -19 | -34 |
| -9 | -16 | -13 | -7 | -9 | -12 | -7 | -19 | -15 | -11 | -21 | -14 | -16 |
Соответствующие значения Y:
| -3 | -3 | -3 | -1 | |||||||||||||
| -1 | -3 | |||||||||||||||
4.
Вариант №6
1. Из чисел 1, 2, 3, 4, 5, 6, 7, 8 наудачу выбирают три числа. Какова вероятность того, что их произведение нечетно?
2. Студент выучил половину из 20 экзаменационных вопросов. На экзамене студент получает случайным образом 2 из 20 вопросов. Случайная величина X – число вопросов на экзамене, ответы на которые знал студент. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости выносливости образцов стали Y (в сотнях кг/мм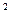 
) от предела прочности X (в сотнях кг/мм ):
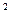Значения X:
| 1.0 | 1.6 | 1.0 | 1.7 | 1.4 | 1.5 | 0.9 | 1.4 | 0.8 | 0.6 | 1.2 | 1.4 | 1.9 | 0.8 | 1.2 | 0.6 | 0.6 |
| 1.0 | 1.0 | 0.9 | 1.6 | 0.2 | 0.4 | 0.7 | 1.6 | 0.8 | 1.4 | 1.1 | 1.0 | 1.0 | 0.8 | 0.4 | 1.4 | 0.6 |
| 0.6 | 1.0 | 0.7 | 1.6 | 1.4 | 0.7 | 1.3 | 1.3 | 1.2 | 1.7 | 0.9 | 1.2 | 1.2 | 2.1 | 1.6 | 1.2 |
Соответствующие значения Y:
| 0.36 | 0.55 | 0.45 | 0.57 | 0.36 | 0.54 | 0.44 | 0.52 | 0.36 | 0.40 | 0.48 | 0.52 | 0.60 | 0.42 | 0.49 | 0.39 | 0.39 |
| 0.45 | 0.45 | 0.44 | 0.56 | 0.49 | 0.37 | 0.40 | 0.55 | 0.43 | 0.53 | 0.48 | 0.46 | 0.45 | 0.43 | 0.63 | 0.51 | 0.40 |
| 0.39 | 0.63 | 0.41 | 0.56 | 0.52 | 0.63 | 0.50 | 0.51 | 0.48 | 0.57 | 0.44 | 0.48 | 0.49 | 0.63 | 0.55 | 0.49 |
Вариант №7
1. Игрок выигрывает, если в результате подбрасывания двух игральных костей набирает в сумме число большее или равное 10. Найти вероятность выигрыша в одной игре.
|
|
|
2. Стрелку дается три патрона. Он стреляет по мишени до первого попадания, причем вероятность поражения мишени при каждом выстреле равна 0,65. Случайная величина X – число использованных патронов. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости коэффициента обрабатываемости Y от ударной вязкости X (в кг/мм 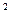) инструментальных быстрорежущих сталей:
Значения X:
| 1.2 | 1.1 | 0.9 | 1.6 | 1.3 | 1.0 | 1.1 | 1.0 | 1.7 | 1.0 | 1.3 | 1.0 | 1.1 | 1.2 | 0.9 | 1.0 | 1.2 |
| 1.3 | 0.6 | 1.6 | 1.3 | 1.1 | 1.0 | 1.2 | 1.3 | 1.4 | 0.6 | 1.1 | 1.2 | 1.0 | 0.9 | 1.0 | 0.9 | 0.9 |
| 1.2 | 1.1 | 1.0 | 1.4 | 1.2 | 1.3 | 1.0 | 0.7 | 1.1 | 1.0 | 1.1 | 1.0 | 1.1 | 1.1 | 0.9 | 0.9 |
Соответствующие значения Y:
| 0.56 | 0.71 | 0.66 | 0.82 | 0.56 | 0.67 | 0.70 | 0.69 | 0.56 | 0.67 | 0.75 | 0.67 | 0.70 | 0.73 | 0.65 | 0.67 | 0.73 |
| 0.76 | 0.56 | 0.61 | 0.75 | 0.70 | 0.67 | 0.72 | 0.74 | 0.76 | 0.59 | 0.69 | 0.72 | 0.68 | 0.66 | 0.83 | 0.64 | 0.65 |
| 0.72 | 0.83 | 0.67 | 0.78 | 0.73 | 0.83 | 0.67 | 0.62 | 0.70 | 0.68 | 0.69 | 0.68 | 0.70 | 0.70 | 0.66 | 0.65 |
Вариант №8
1. В шкаф поставили 6 новых одинаковых приборов. Для проведения опыта берут наугад 3 прибора, после работы их возвращают в шкаф. Определите вероятность того, что после проведения двух опытов в шкафу не останется неиспользованных приборов.
2. Эксперт проверяет качество товара в партии из трех изделий. Вероятность того, что изделие окажется бракованным равна 0,15. Случайная величина X – число бракованных изделий в этой партии. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости стойкости сверл Y (в минутах) от толщины сердцевины X (в мм):
Значения X:
| 0.81 | 0.82 | 0.77 | 0.83 | 0.78 | 0.81 | 0.84 | 0.92 | 0.86 | 0.91 | 0.73 | 0.82 | 0.83 | 0.79 | 0.87 | 0.82 | 0.79 |
| 0.89 | 0.77 | 0.85 | 0.85 | 0.86 | 0.85 | 0.88 | 0.80 | 0.85 | 0.84 | 0.89 | 0.73 | 0.83 | 0.87 | 0.79 | 0.87 | 0.81 |
| 0.82 | 0.74 | 0.83 | 0.86 | 0.83 | 0.84 | 0.78 | 0.90 | 0.89 | 0.78 | 0.91 | 0.76 | 0.83 | 0.80 | 0.78 | 0.83 |
Соответствующие значения Y:
Вариант №9
1. С конвейера сошло 10 изделий, причем два из них содержат брак. Для проверки случайным образом было выбрано три изделия. Найти вероятность того, что среди них окажется одно бракованное.
2. Спортсмен бросает мяч в баскетбольную корзину 3 раза. Вероятность попадания каждый раз равна 0,75. Случайная величина X – число попаданий. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. Даны результаты исследования зависимости веса чугунной плитки Y (в кг) от ее длины X (в см):
|
|
|
Значения X:
Соответствующие значения Y:
| 22.9 | 47.2 | 39.9 | 35.0 | 32.6 | 38.5 | 36.9 | 22.9 | 44.5 | 42.2 | 42.2 | 37.2 | 42.6 | 31.0 | 47.2 | 31.0 | 34.2 |
| 32.6 | 30.9 | 39.0 | 31.3 | 44.9 | 48.5 | 28.2 | 29.2 | 33.5 | 32.4 | 32.5 | 22.9 | 38.1 | 50.9 | 37.2 | 46.1 | 45.0 |
| 50.9 | 43.7 | 50.9 | 39.6 | 50.9 | 43.7 | 37.6 | 40.8 | 43.2 | 41.1 | 30.9 | 39.3 | 38.4 | 42.1 | 32.5 | 22.9 |
Вариант №10
1. При одном цикле обзора радиолокационной станции объект обнаруживают с вероятностью 0,2. Обнаружение объекта в каждом цикле происходит независимо от других. Найти вероятность того, что при двух циклах объект будет обнаружен ровно один раз.
2. Два стрелка стреляют по одной мишени. Вероятность попадания для первого стрелка равна 0,7, а для второго – 0,6. Случайная величина X – общее число попаданий при одном залпе. Составить ее закон распределения, найти математическое ожидание и дисперсию этой случайной величины.
3. В результате экспериментального исследования зависимости времени трелевки Y (в мин) от расстояния трелевки X (в м) получены следующие результаты:
Значения X:
Соответствующие значения Y:
| 3.86 | 5.11 | 4.80 | 4.38 | 3.86 | 4.26 | 5.19 | 4.71 | 3.86 | 4.33 | 4.70 | 4.63 | 4.47 | 4.32 | 5.18 | 4.96 | 4.68 |
| 4.72 | 4.62 | 4.71 | 5.55 | 4.53 | 4.60 | 5.12 | 4.68 | 4.40 | 4.12 | 4.78 | 4.35 | 4.04 | 5.02 | 5.55 | 5.04 | 5.22 |
| 4.29 | 5.35 | 4.75 | 5.00 | 4.80 | 5.35 | 5.35 | 4.28 | 3.86 | 4.71 | 4.26 | 4.83 | 4.39 | 4.95 | 4.65 | 4.92 |
|
|
|
