 |
Системы линейных уравнений
|
|
|
|
7. Система линейных уравнений, ее решения
8. Nтипы систем линейных уравнений. Матричная запись системы линейных уравнений.
9. Метод обратной матрицы.
10. Теорема Крамера, формулы Крамера.
11. Ранг матрицы, элементарные преобразования матриц, расширенная матрица.
12. Общая теория систем линейных уравнений, теорема Кронекера-Капелли.
13. Метод последовательного исключения переменных Гаусса.
Основы аналитической геометрии
14. Понятие вектора. Операции над векторами.
15. Линейная зависимость векторов, базис.
16. Скалярное произведение векторов.
17. Векторное произведение векторов.
18. Смешанное произведение векторов.
19. Уравнения прямой на плоскости.
20. Уравнения плоскости в пространстве.
21. Плоскость и прямая в пространстве.
22. Кривые второго порядка: эллипс, гипербола, парабола.
23. Инварианты кривых второго порядка
Рекомендуемая литература
1. Канатников А.Н., Крищенко А.П. Линейная алгебра. М., Изд. МГТУ им. Н.Э. Баумана, 1999.
2. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М., Изд. МГТУ им. Н.Э. Баумана, 1999.
3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 1984.
4. Ильин В.А., Позняк Э.Г. Линейная алгебра. М., Наука, 1988.
5. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М., Наука, 1988.
6. Сборник задач по математике для втузов. Ч. 1. Под общ. ред. А.В. Ефимова и Б.П.Демидовича. М., Наука, 1993.
7. Проскуряков И.В. Сборник задач по линейной алгебре. М., Наука, 1974.
8. Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел. М., Просвещение, 1993.
Контрольное задание
(№ варианта равен последней цифре номера зачётной книжки, вар. 10 соответствует цифре 0)
1 задание. Вычислить определитель матрицы  :
:
|
|
|
I вар.

| II вар.
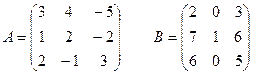
|
III вар.

| IV вар.

|
V вар.

| VI вар.

|
VII вар.

| VIII вар.

|
IX вар.

| X вар.

|
Задание. Найти обратную матрицу
I вар.

| II вар.

| III вар.

| IV вар.

| V вар.

|
VI вар.

| VII вар.

| VIII вар.

| IX вар.

| X вар.

|
Задание. Решить систему линейных уравнений методом Гаусса
I вар.

| II вар.

|
III вар.

| IV вар.

|
V вар.

| VI вар.

|
VII вар.

| VIII вар.

|
IX вар.

| X вар.

|
4 задание. Даны три вектора p = {3; -2; 1}, q = {-1; 1; -2}, r = {2; 1; -3}
Найти разложение вектора c по базису p, q, r.
| Вариант 1-3 | Вариант 4-6 | Вариант 7-10 |
c = {11; -6; 5} c = {9; -6; 4} c = {-7; -7; 5}
5 задание. Составить каноническое уравнение прямой
| Вариант 1-3 | Вариант 4-6 | Вариант 7-10 |



6 задание. При каких значениях m и n уравнение определяет:
1. Центральную линию;
2. Линию без центра;
3. Линию, имеющую бесконечно много центров.
| Вариант 1-3 | x2 + 6xy + my2 + 3x + ny – 4 = 0 |
| Вариант 4-6 | mx2 + 12xy + 9y2 + 4x + ny – 13 = 0 |
| Вариант 7-10 | 5x2 + 14xy + my2 + 20x + ny – 18 = 0 |
Семестр
Теория вероятностей
Случайные события и процессы.
1. Испытания и события, виды случайных событий.
2. Классическое и статистическое определения вероятности, свойства вероятности.
3. Элементы комбинаторики.
4. Сумма событий, сложение вероятностей.
5. Противоположные события.
6. Произведение событий, условная вероятность, умножение вероятностей, независимые события.
7. Формула полной вероятности.
8. Формула Бейеса.
9. Повторные независимые испытания, формула Бернулли.
10. Локальная теорема Лапласа.
11. Интегральная теорема Лапласа.
12. Теорема Пуассона.
13. Случайные процессы.
Случайные величины.
14. Дискретная случайная величина, ее закон распределения.
15. Функция распределения, ее свойства.
16. Математическое ожидание, дисперсия, среднее квадратичное отклонение дискретной случайной величины, их свойства.
|
|
|
17. Моменты.
18. Непрерывная случайная величина.
19. Плотность распределения вероятностей, ее свойства.
20. Числовые характеристики непрерывной случайной величины.
21. Закон больших чисел, теорема Чебышева.
22. Центральная предельная теорема.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Статистические оценки.
23. Генеральная и выборочная совокупности. Статистическое распределение выборки.
24. Эмпирическая функция распределения, ее свойства. Статистические оценки.
25. Типы оценок. Точечная оценка. Выборочная средняя.
26. Выборочная дисперсия. Метод наибольшего правдоподобия.
27. Интервальная оценка. Доверительный интервал для оценки математического ожидания нормального распределения при известном и при неизвестном среднем квадратичном отклонении, среднего квадратичного отклонения нормального распределения, вероятности биномиального распределения.
|
|
|


