 |
Метод обыкновенных жордановых исключений
|
|
|
|
ПРИЛОЖЕНИЯ
Контрольное задание №1.……………………….……………………………64
Контрольное задание №2.……………………….……………………………66
Контрольное задание №3.……………………….……………………………67
Литература…………………………………………………...………………..70
ВВЕДЕНИЕ
Наиболее простым методом преобразования систем линейных уравнений традиционно считается метод Гаусса-Жордана. При помощи данного метода можно найти единственное решение системы линейных уравнений или доказать его отсутствие. А в том случае, когда система имеет бесчисленное множество решений, метод Гаусса-Жордана позволяет находить базисные решения системы и переходить всего за один шаг от одного базисного решения к другому. Такая особенность метода Гаусса-Жордана позволила на его основе реализовать так называемый симплекс-метод решения задач линейного программирования.
Однако существует еще один метод преобразования систем линейных уравнений – метод жордановых исключений. По существу, это хорошо всем нам знакомый метод исключения неизвестных. Однако практическая реализация данного метода в виде жордановых таблиц позволила существенно сократить арифметические вычисления. Это заметно даже при решении задач линейной алгебры. Но особенно это заметно во время решения задач математического программирования. Применительно к задачам линейного программирования, метод жордановых исключений получил название метода Штифеля.
Метод Штифеля успешно применяется в математическом программировании не только потому, что он существенно проще традиционного симплекс-метода. Самое главное его достоинство заключается в том, что он позволяет примерно вдвое сократить количество учебных часов, необходимых преподавателю для прочтения курса линейного программирования.
|
|
|
Пособие состоит из четырех частей. В первой части изучаются методы жордановых исключений и модифицированных жордановых исключений. Данные методы преобразования систем линейных равенств оформляются в виде жордановых таблиц. Приведены и доказаны алгоритмы перехода от одной жордановой таблицы к другой (один шаг жордановых исключений).
Во второй главе изучаются применение метода жордановых исключений в линейной алгебре. Применение метода жордановых исключения к решению стандартных задач линейной алгебры оказалось вполне оправданным. На примерах доказано, что решение таких задач, как вычисление ранга матрицы, нахождение обратной матрицы и решение систем линейных уравнений методом жордановых исключений оказалось проще, чем решение традиционными методами.
В третьей и четвертой главе данного пособия содержится краткое изложение курса математического программирования, основанного на методе жордановых исключений (метод Штифеля).
Пособие, прежде всего, предназначено для студентов математических факультетов, получающих специальность «Преподаватель». Данное пособие также полезно студентам экономических и других специальностей, изучающих математическое программирование и линейную алгебру.
ГЛАВА I
МЕТОД ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ
Метод обыкновенных жордановых исключений
Пусть дана система линейных форм (уравнений):
a 11 x 1 + a 12 x 2 +…+ a 1 jxj + … + a 1 sxs + … + a 1 nxn = y 1,
………………………………………………………….
ai 1 x 1 + ai 2 x 2 +…+ aijxj + …+ aisxs + … + ainxn = yi,
………………………………………………………….
ar 1 x 1 + ar 2 x 2 + …+ arjxj +… + arsxs + … + arn xn = yr, (1.1)
………………………………………………………….
am 1 x 1 + am 2 x 2 +…+ amjxj + … + amsxs + …+ amnxn = ym,
где aij – постоянные коэффициенты (i = 1, 2,…, m; j = 1, 2,…, n).
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного
(r -го) равенства выразим произвольную переменную (xs) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда ars ¹ 0. Коэффициент ars называется разрешающим (иногда направляющим или главным) элементом. Мы получим следующую систему:
|
|
|
b 11 x 1 + b 12 x 2 +…+ b 1 jxj + … + b 1 syr + … + b 1 nxn = y 1,
………………………………………………………….
bi 1 x 1 + bi 2 x 2 +…+ bijxj + …+ bisyr + … + binxn = yi,
………………………………………………………….
br 1 x 1 + br 2 x 2 + …+ brjxj +… + brsyr + … + brn xn = xs, (1.2)
………………………………………………………….
bm 1 x 1 + bm 2 x 2 +…+ bmjxj + … + bmsyr + …+ bmnxn = ym.
Вычислим коэффициенты полученной системы (1.2) через коэффициенты исходной системы (1.1). Начнем с r -го уравнения, которое после выражения переменной xs через остальные переменные будет выглядеть следующим образом:
. (1.3)
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.4)
Вычислим теперь новые коэффициенты bij (i ¹ r) произвольного уравнения. Для этого подставим выраженную в (1.3) переменную xs в
i -е уравнение системы (1.1):
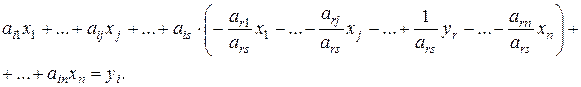
После приведения подобных членов, получим:
(1.5)
Из равенства (1.5) получим формулы, по которым вычисляются остальные коэффициенты системы (1.2) (за исключением r -го уравнения):
(1.6)
Как и в случае решения линейных уравнений, методом Гаусса, преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых». Так, задаче (1.1) ставится в соответствие следующая жорданова таблица:
| x 1 | x 2 | … | xj | … | xs | … | xn | |
| y 1 | a 11 | a 12 | a 1 j | a 1 s | a 1 n | |||
| ………………………………………………………………….. | ||||||||
| yi | ai 1 | ai 2 | aij | ais | ain | |||
| ………………………………………………………………….. | ||||||||
| yr | ar 1 | ar 2 | arj | ars | arn | |||
| …………………………………………………………………. | ||||||||
| yn | am 1 | am 2 | amj | ams | amn |
Табл. 1.1.
Системе (1.2) при этом соответствует жорданова таблица:
| x 1 | x 2 | … | xj | … | yr | … | xn | |
| y 1 | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| yi | bi 1 | bi 2 | bij | bis | bin | |||
| ………………………………………………………………….. | ||||||||
| xs | br 1 | br 2 | brj | brs | brn | |||
| …………………………………………………………………. | ||||||||
| yn | bm 1 | bm 2 | bmj | bms | bmn |
Табл. 1.2.
|
|
|
Разрешающий элемент ars мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений соответствующий разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. Независимые переменные x 1, x 2,…, xn записывают в верхней заглавной строке таблицы. Зависимые переменные y 1, y 2,…, yn – в левом заглавном столбце. При переходе от данной таблицы к следующей одна переменная из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, одна переменная из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку. То есть меняются местами переменные, содержащиеся в разрешающем столбце и разрешающей строке.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.4) и (1.6).
1. Разрешающий элемент заменяется обратным числом: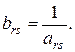 
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный: 
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент: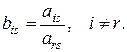 
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам: 
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь 
, находятся на пересечении i –ой и r –ой строк и j –го и s –го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы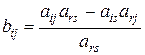 
можно использовать следующую диаграмму:
| aij | ais | ||
| + | – | ||
| arj | ars |
Пример 1.1. Пусть дана система равенств:
4 x 1 + 2 x 2 – 7 x 3 + 6 x 4 = y 1,
8 x 1 + 5 x 2 + 4 x 3 – 6 x 4 = y 2,
3 x 1 – 4 x 2 + 5 x 3 + 9 x 4 = y 3.
|
|
|
Данную систему можно записать в виде следующей жордановой таблицы:
| x 1 | x 2 | x 3 | x 4 | |
| y 1 | -7 | |||
| y 2 | -6 | |||
| y 3 | -4 |
Табл. 1.3.
Выберем в качестве разрешающего элемента число 5, находящееся на пересечении 3-ей строки и 3-го столбца. При этом переменная x 3 меняется с переменной y 3 местами, и мы получим новую таблицу:
| x 1 | x 2 | y 3 | x 4 | |
| y 1 | 8,2 | -3,6 | -1,4 | 18,6 |
| y 2 | 5,6 | 8,2 | 0,8 | -13,2 |
| x 3 | -0,6 | 0,8 | 0,2 | -1,8 |
Табл. 1.4.
Подробно поясним, как были получены коэффициенты новой системы.
1. Разрешающий элемент заменился на обратное число:
2. Остальные элементы разрешающей строки вычислялись по формуле:
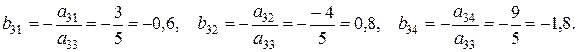
3. Остальные элементы разрешающего столбца вычислялись по формуле:
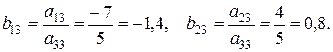
4. Остальные коэффициенты системы пересчитывались по формулам:
|
|
|
