 |
Решение систем линейных уравнений
|
|
|
|
Решать системы линейных уравнений с помощью метода обыкновенных Жордановых исключений можно одним из четырех способов. Проиллюстрируем эти способы на одном простом примере.
Пример 2.3. Решить систему линейных уравнений:
3 x + 2 y + 4 z = –5,
2 x – 3 y + z = –7, (2.1)
–3 x + 4 y + 2 z = –1.
Решение. Первый способ.
Запишем систему в виде жордановой таблицы (табл. 2.9):
| x | y | z | x | y | –7 | ||||
| –5 | –5 | –5 | |||||||
| –7 | –3 | z | –2 | ||||||
| –1 | –3 | –1 | –7 |
Табл. 2.9. Табл. 2.10.
При переходе от таблицы 2.9 к таблице 2.10 выберем в качестве разрешающего элемента число a 23 = 1 (при этом переменная z поменяется местами с –7). При переходе к следующей таблице 2.11 выберем в качестве разрешающего элемента число a 11 = – 5.
| –5 | y | –7 | –5 | –1 | –7 | ||||
| x | –0,2 | 2,8 | 0,8 | x | 10/48 | –14/48 | –12/48 | ||
| z | 0,4 | –2,6 | –0,6 | z | 1/48 | 13/48 | 18/48 | ||
| –1 | 1,4 | –9,6 | –3,6 | y | 7/48 | –5/48 | –18/48 |
Табл. 2.11. Табл. 2.12.
При переходе от таблицы 2.11 к таблице 2.12 выберем в качестве разрешающего элемента число a 32 = – 9,6 (при этом последняя, оставшаяся наверху, переменная y опускается вниз). Из последней таблицы находим решение системы:

Первый способ выглядит достаточно громоздким, чем широко распространенный метод Гаусса. Но не спешите с выводами.
Второй способ. Второй способ отличается от первого только тем, что мы будем последовательно запоминать некоторые строки и исключать их из таблицы (т. е. не пересчитывать соответствующие элементы). Тем самым мы существенно сократим наши вычисления, поскольку будем запоминать (вычеркивать) те строки, в которые опускаются переменные из верхней части таблицы:
|
|
|
| x | y | z | x | y | –7 | ||||
| –5 | –5 | –5 | |||||||
| –7 | –3 | z | –2 | ||||||
| –1 | –3 | –1 | –7 |
Табл. 2.13. Табл. 2.14.
| –5 | y | –7 | –5 | –1 | –7 | ||||
| x | –0,2 | 2,8 | 0,8 | y | 7/48 | –5/48 | –18/48 | ||
| –1 | 1,4 | –9,6 | –3,6 | Табл. 2.16. |
Табл. 2.15.
Из последней таблицы 2.16 находим y:
 .
.
Подставляя y в последнюю из запомненных строк, найдем x:
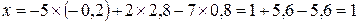 .
.
Подставляя найденные переменные x и y в первую запомненную строку, найдем z:
 .
.
Третий способ. Этот способ отличается от предыдущих способов тем, что на первом этапе задача усложняется за счет введения дополнительного столбца. Но затем на каждом шаге таблица уменьшается на один столбец. Это происходит из-за того, что на каждом шаге в верхнюю строку таблицы попадает ноль. В таком случае числа соответствующего столбца можно больше не пересчитывать (какими бы эти числа не оказались, они все равно умножаются на ноль).
Перепишем систему в виде:
3 x + 2 y + 4 z +5 = 0
2 x – 3 y + z +7 = 0 (2.2)
–3 x + 4 y + 2 z +1 = 0
Решение данной задачи методом обыкновенны жордановых исключений будет выглядеть следующим образом:
| x | y | z | x | y | |||||
| –5 | –23 | ||||||||
| –3 | z | –2 | –7 | ||||||
| –3 | –7 | –13 |
Табл. 2.17. Табл. 2.18.
| x | x | |||||
| 4,8 | 4,8 | –4,8 | x | |||
| z | 0,1 | 0,1 | –3,1 | z | –3 | |
| y | 0,7 | 0,7 | 1,3 | y |
Табл. 2.19. Табл. 2.20.
Из последней таблицы 2.20 сразу находим решение:
x = 1,
y = 2,
z = –3.
Однако наиболее простым является комбинация второго и третьего способа (назовем это четвертым способом). В данном случае таблица на каждом шаге «тает» на одну строку и на один столбец. Такой подход к решению систем линейных уравнений является наиболее коротким.
|
|
|
Четвертый способ. Как и в предыдущем случае приведем систему к виду (1.2). Решая данную задачу методом обыкновенных жордановых исключений, на каждом шаге будем исключать из таблицы столбец, верхний заглавный элемент которого становится равным нулю, и запоминать строку, левый заглавный элемент которой совпадает с переменной:
| x | y | z | x | y | |||||
| –5 | –23 | ||||||||
| –3 | z | –2 | –7 | ||||||
| –3 | –7 | –13 |
Табл. 2.21. Табл. 2.22.
| x | |||||
| 4,8 | –4,8 | ||||
| y | 0,7 | 1,3 | x |
Табл. 2.23. Табл. 2.24.
Из последней таблицы 2.24 находим x = 1.
Из предпоследней таблицы 2.23 находим y = 1´0,7 + 1´1,3 = 2.
И, наконец, из таблицы 2.22 находим z = 1´(–2) + 2´3 + 1´(–7) = –3.
Рассмотрим более сложный пример.
Пример 2.4. Решить систему линейных уравнений:
2 x 1 + 3 x 2 – 4 x 3 + x 4 – 2 x 5 + 2 = 0,
3 x 1 + 4 x 2 + 2 x 4 + x 5 – 3 = 0,
–4 x 1 + 2 x 2 – 2 x 3 + 3 x 4 – 3 x 5 – 5 = 0. (2.3)
x 1 + 3 x 2 + 3 x 3 – 3 x 4 – x 5 + 3 = 0,
5 x 1 + 2 x 2 – 2 x 3 + x 4 – 3 x 5 – 8 = 0.
Решение. Запишем систему в виде жордановой таблицы (табл. 2.25):
| x 1 | x 2 | x 3 | x 4 | x 5 | x 1 | x 2 | x 3 | x 4 | |||||
| –4 | –2 | –4 | –4 | ||||||||||
| –3 | x 5 | –3 | –4 | –2 | |||||||||
| –4 | –2 | –3 | –5 | –2 | –14 | ||||||||
| –3 | –1 | –1 | |||||||||||
| –2 | –3 | –8 | –2 | –17 |
Табл. 2.25. Табл. 2.26.
При переходе от таблицы 2.25 к следующей таблице 2.26 (в качестве разрешающего элемента выбираем коэффициент при переменной x 5 во втором уравнении) вычеркиваем предпоследний столбец (в верхнюю часть которого попадает ноль). Запоминая строку x 5, переходим к таблице 2.27. Всего через пять шагов, на каждом из которых одна из переменных из верхней заглавной строки таблицы попадает в левый заглавный столбец, мы приходим к таблице 2.30, содержащей только одну строку и один столбец:
| x 1 | x 2 | x 3 | x 1 | x 2 | |||||
| –4 | 9,96 | 12,12 | 2,16 | ||||||
| –14 | x 3 | –1,64 | –3,08 | 0,56 | |||||
| x 4 | 10,84 | 4,48 | –6,36 | ||||||
| –17 | Табл. 2.28. |
Табл. 2.27.
|
|
|
| x 1 | |||||
| x 2 | –83/101 | –18/101 | x 1 | ||
| 723/101 | –723/101 | Табл. 2.30. |
Табл. 2.29.
Из таблицы 2.30 находим x 1 = 1. Подставляя x 1 в последнюю запомненную нами строку (табл.2.29), найдем x 2. Подставляя x 1 и x 2 в предпоследнюю запомненную строку (табл.2.28), найдем x 3, и так далее.
 .
.
x 3 = –1,64´1 –3,08´(–1) + 0,56´1 = 3,64 – 1,64 = 2.
x 4 = 4´1 + 7´(–1) + 3´2 + 0´1 = 4 – 7 + 6 = 3.
x 5 = –3´1 – 4´(–1) + 0´2 – 2´3 + 3´1 = -3 + 4 – 6 + 3 = – 2.
Искушенный читатель заметит, что бывают еще системы линейных уравнений, имеющие бесчисленное количество решений или вовсе не имеющие таковых. Однако и в этих ситуациях вполне применим метод обыкновенных жордановых исключений. Приведем следующие примеры:
Пример 2.5. Решить систему линейных уравнений:
3 x 1 + 2 x 2 – 4 x 3 + 3 x 4 + x 5 – 9 = 0,
2 x 1 – 3 x 2 – 2 x 3 – 2 x 4 + 5 x 5 + 7 = 0,
–5 x 1 – 4 x 2 + x 3 – 2 x 4 + 4 x 5 – 9 = 0, (2.4)
4 x 1 – 6 x 2 – 5 x 3 – 3 x 4 + 9 x 5 + 8 = 0.
Решение. Систему будем решать четвертым способом, описанным в примере 2.3. При этом нас не должно смущать то обстоятельство, что количество уравнений в системе (2.4) не совпадает с числом неизвестных. Запишем систему в виде жордановой таблицы (табл. 2.31):
| x 1 | x 2 | x 3 | x 4 | x 5 | x 1 | x 2 | x 4 | x 5 | |||||
| –4 | –9 | –17 | –14 | –5 | –45 | ||||||||
| –3 | –2 | –2 | –8 | –11 | –6 | –11 | |||||||
| –5 | –4 | –2 | –9 | x 3 | –4 | ||||||||
| –6 | –5 | –3 | –21 | –26 | –13 | –37 |
Табл. 2.31. Табл. 2.32.
При переходе от таблицы 2.31 к таблице 2.32 в качестве разрешающего элемента выбираем коэффициент при переменной x 3 в третьем уравнении. Запоминая строку x 3, переходим к таблице 2.33. И так далее.
| x 1 | x 2 | x 5 | x 1 | x 5 | |||||
| x 4 | –3,4 | –2,8 | 3,4 | –9 | x 2 | –62/29 | 37/29 | –215/29 | |
| 12,4 | 5,8 | –7,4 | 28/29 | –56/29 | 84/29 | ||||
| 23,2 | 10,4 | –15,2 | Табл. 2.34. |
Табл. 2.33.
| x 5 | ||
| x 1 | –3 |
Табл. 2.35.
Из последней таблицы 2.35 находим: x 1 = – 3 + 2 x 5.
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
|
|
|


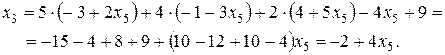
Таким образом, система имеет бесчисленное множество решений. Придавая переменной x 5, выступающей в роли параметра, произвольные значения, мы получаем различные решения системы. Переменная x 5 называется свободной. Мы доказали совместность системы и нашли ее общее решение:
x 1 = – 3 + 2 x 5,
x 2 = – 1 – 3 x 5,
x 3 = – 2 + 4 x 5, (2.5)
x 4 = 4 + 5 x 5.
Придавая свободной переменной нулевое значение, мы получим одно из базисных решений системы (– 3; – 1; – 2; 4; 0). Если преобразовать систему (2.5) методом жордановых исключений, то можно в качестве свободной переменной получить любую из переменных x 1, x 2, x 3, или x 4. Тем самым мы можем найти еще четыре базисных решения системы (2.4). Предоставляем читателям сделать это самостоятельно.
Приведем пример, в котором с помощью метода обыкновенных жордановых исключений доказывается несовместность системы линейных уравнений.
Пример 2.6. Решить систему линейных уравнений:
3 x 1 + 2 x 2 – 4 x 3 + 3 x 4 + x 5 – 9 = 0,
2 x 1 – 3 x 2 – 2 x 3 – 2 x 4 + 5 x 5 + 7 = 0,
–5 x 1 – 4 x 2 + x 3 – 2 x 4 + 4 x 5 – 9 = 0, (2.6)
3 x 1 + 7 x 2 + x 3 + 4 x 4 – 9 x 5 + 3 = 0.
Решение. Систему по-прежнему будем решать четвертым способом, описанным в примере 2.3. Запишем систему (2.6) в виде жордановой таблицы (табл. 2.36). Некоторое сходство задачи (2.6) с задачей (2.4) позволит читателю не тратить понапрасну время на проверку многих арифметических действий.
| x 1 | x 2 | x 3 | x 4 | x 5 | x 1 | x 2 | x 4 | x 5 | |||||
| –4 | –9 | –17 | –14 | –5 | –45 | ||||||||
| –3 | –2 | –2 | –8 | –11 | –6 | –11 | |||||||
| –5 | –4 | –2 | –9 | x 3 | –4 | ||||||||
| –9 | –13 |
Табл. 2.36. Табл. 2.37.
При переходе от таблицы 2.36 к таблице 2.37 в качестве разрешающего элемента выбираем коэффициент при переменной x 3 в третьем уравнении. Запоминая строку x 3 и выбирая в качестве разрешающего элемента число –5, переходим к таблице 2.38. И так далее.
| x 1 | x 2 | x 5 | x 1 | x 5 | |||||
| x 4 | –3,4 | –2,8 | 3,4 | –9 | x 2 | –62/29 | 37/29 | –215/29 | |
| 12,4 | 5,8 | –7,4 | |||||||
| –12,4 | –5,8 | 7,4 | –42 | Табл. 2.39. |
Табл. 2.38.
Дальнейший перевод переменных из верхней заглавной строки таблицы в левый заглавный столбец невозможен, так как оба разрешающих элемента равны нулю. Но это еще не означает несовместность системы. Необходимо расшифровать «непослушную» строку (строки) таблицы:
0 = 0´ x 1 + 0´ x 5 + 1´1 = 1.
Так как полученное уравнение не выполняется ни при каких значениях x 1, x 2, x 3, x 4, и x 5, то можно сделать вывод о несовместности системы (2.6).
|
|
|
Приведем еще один полезный пример.
Пример 2.7. Решить систему линейных уравнений:
–2 x 1 + x 2 – 4 x 3 + 2 x 4 + 9 = 0,
3 x 1 – 2 x 2 + 5 x 3 + 6 x 4 – 13 = 0,
– x 1 – 3 x 3 + 2 x 4 + 5 = 0, (2.7)
2 x 1 – x 2 + 4 x 3 + 2 x 4 – 9 = 0.
Решение. Запишем систему (2.7) в виде жордановой таблицы
(табл. 2.40).
| x 1 | x 2 | x 3 | x 4 | x 1 | x 3 | x 4 | |||||
| –2 | –4 | –2 | x 2 | –9 | |||||||
| –2 | –13 | –1 | –3 | ||||||||
| –1 | –3 | –1 | –3 | ||||||||
| –1 | –9 |
Табл. 2.40. Табл. 2.41.
При переходе от таблицы 2.40 к таблице 2.41 в качестве разрешающего элемента выбираем коэффициент при переменной x 2 в первом уравнении. Запоминая строку x 2, вычеркивая из системы тождество 0 = 0 и выбирая в качестве разрешающего элемента коэффициент при переменной x 1 во втором уравнении, переходим к таблице 2.42:
| x 3 | x 4 | x 3 | x 4 | |||||
| x 1 | –3 | x 1 | –3 | |||||
| Табл. 2.43. | ||||||||
Табл. 2.42.
Перевод переменных x 3 и x 4 из верхней строки таблицы в левый столбец невозможен, так как все четыре разрешающих элемента равны нулю. Рассмотрим две последние строки таблицы:
0 = 0´ x 3 + 0´ x 4 + 0´1 = 0,
0 = 0´ x 3 + 0´ x 4 + 0´1 = 0.
Так как данные строки являются тождествами, то их можно исключить из таблицы 2.42. Окончательно мы получаем таблицу 2.43, из которой находим:
x 1 = –3 x 3 + 2 x 4 + 5.
Подставляя в запомненную строку из таблицы 2.41, получим:
x 2 = 2´ (–3 x 3 + 2 x 4 + 5) + 4 x 3 + 2 x 4 – 9 = –2 x 3 + 6 x 4 + 1.
Итак, мы доказали, что система (2.6) совместна, и ее общим решением является:
x 1 = –3 x 3 + 2 x 4 + 5,
x 2 = –2 x 3 + 6 x 4 + 1.
Переменные x 3 и x 4 играют роль параметров. Подставляя вместо них любые числа, мы получим бесчисленное множество решений системы.
|
|
|


