 |
Линейного программирования
|
|
|
|
Вернемся к общей задаче линейного программирования:
f (X) = c 1 x 1 + c 2 x 2 + … + cnxn ® max, (4.7)
a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 nxn £ b 1,
…………………………………………
ak 1 x 1 + ak 2 x 2 + ak 3 x 3 + … + aknxn £ bk,
ak+ 1;1 x 1 + ak+ 1;2 x 2 + … + ak+ 1; n xn = bk+ 1, (4.8)
………………………………………….
am 1 x 1 + am 2 x 2 + am 3 x 3 + … + amnxn = bm,
x 1, x 2, x 3, …, xs ³ 0.
Без ограничения общности мы будем как и раньше предполагать, что исходная задача является задачей на максимум. Первые k ограничений являются неравенствами вида £, остальные n – k ограничений являются равенствами, и первые s переменных ограничены на знак.
Двойственной задачей к задаче (4.7) – (4.8) называется задача
j (Y) = b 1 y 1 + b 2 y 2 + … + bmym ® min, (4.9)
a 11 y 1 + a 21 y 2 + a 31 y 3 + … + am 1 ym ³ c 1,
…………………………………………
a 1 sx1 + a 2 sy2 + a 3 sy 3 + … + amsym ³ cs,
a 1; s+ 1 y 1 + a 2; s+ 1 y 2 + … + am ; s + 1 ym = cs+ 1, (4.10)
………………………………………….
a 1 nx1 + a 2 ny2 + a 3 ny 3 + … + amnym = cn,
y 1, y 2, y 3, …, yk ³ 0.
Количество ограничений двойственной задачи совпадает с числом переменных исходной задачи, а число переменных двойственной задачи совпадает с количеством ограничений исходной задачи. Тем самым устанавливается соответствие между ограничениями и переменными взаимно двойственных задач (несколько позднее мы докажем, что задача, двойственная к двойственной задаче, совпадает с исходной).
Двойственная задача (4.9) – (4.10) строится по следующему правилу:
1. Пусть исходная задача является задачей на максимум с ограничениями, являющимися равенствами, или неравенствами вида £. Тогда двойственная задача является задачей на минимум с ограничениями, являющимися равенствами, или неравенствами вида ³.
2. Коэффициенты функции цели (4.9) являются правыми частями системы ограничений (4.8) исходной задачи.
|
|
|
3. Правые части системы ограничений (4.10) двойственной задачи совпадают с коэффициентами функции цели (4.7) исходной задачи.
4. Матрица системы ограничений (4.10) является транспонированной матрицей системы (4.8).
5. Те ограничения двойственной задачи, которые соответствуют ограниченным на знак переменным исходной задачи, имеют вид неравенств вида ³. Остальные ограничения двойственной задачи являются равенствами.
6. Те переменные двойственной задачи, которые соответствуют ограничениям исходной задачи вида £, ограничены на знак. Остальные переменные двойственной задачи ограничений на знак не имеют.
Теорема 5.1. Задача, двойственная к задаче (4.9) – (4.10), совпадает с исходной задачей (4.7) – (4.8).
Доказательство. Переформулируем задачу (4.9) – (4.10), превратив ее в задачу на максимум с ограничениями, являющимися равенствами или неравенствами вида £. Для этого умножим все ограничения (4.10) на (–1), и рассмотрим новую функцию цели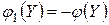 
. При этом 
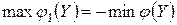. Таким образом, мы приходим к следующей задаче:
j 1(Y) = – b 1 y 1 – b 2 y 2 – … – bmym ® max, (4.11)
– a 11 y 1 – a 21 y 2 – a 31 y 3 – … – am 1 ym ³ – c 1,
……………………………………………
– a 1 sx1 – a 2 sy2 – a 3 sy 3 – … – amsym ³ – cs,
– a 1; s+ 1 y 1 – a 2; s+ 1 y 2 – … – am ; s + 1 ym = – cs+ 1, (4.12)
…………………………………………….
– a 1 nx1 – a 2 ny2 – a 3 ny 3 – … – amnym = – cn,
y 1, y 2, y 3, …, yk ³ 0.
Составим двойственную задачу к задаче (4.11) – (4.12), обозначив двойственные переменные через xi, а функцию цели через f 1(X):
f1 (X) = – c 1 x 1 – c 2 x 2 – … – cnxn ® min, (4.13)
– a 11 x 1 – a 12 x 2 – a 13 x 3 – … – a 1 nxn £ – b 1,
………………………………….….………
– ak 1 x 1 – ak 2 x 2 – ak 3 x 3 – … – aknxn £ – bk,
– ak+ 1;1 x 1 – ak+ 1;2 x 2 – … – ak+ 1; n xn = – bk+ 1, (4.14)
……………………………….…………….
– am 1 x 1 – am 2 x 2 – am 3 x 3 – … – amnxn = – bm,
x 1, x 2, x 3, …, xs ³ 0.
Очевидно, что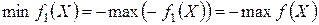 
. Следовательно, умножая функцию цели и ограничения задачи (4.13) – (4.14) на (–1), мы получаем исходную задачу (4.7) – (4.8). Ч.т.д.
|
|
|
При решении различных экономических задач мы зачастую сталкиваемся с необходимостью решать сразу две взаимно-двойственные задачи.
Так, взаимно двойственными являются задачи об использовании сырья или его продажи [3]. В теории игр взаимно двойственные задачи решают конкурирующие стороны.
Оказывается, решение задачи, двойственной к исходной, можно искать методом Штифеля параллельно с решением основной задачи. При этом используются одни и те же жордановы таблицы. Необходимо только в жорданову таблицу ввести один дополнительный заглавный столбец и одну дополнительную заглавную строку. При одном шаге метода Штифеля основная задача преобразуется с помощью модифицированных жордановых исключений. При этом двойственная задача преобразуется методом обыкновенных жордановых исключений. Подробнее о таком методе решения взаимно-двойственных задач можно прочитать в [2].
В частности, таким способом доказаны следующие теоремы двойственности (мы их приводим без доказательства):
Теорема 5.2. Если одна из двойственных задач имеет оптимальное решение, то и другая его имеет, причем экстремальные значения их функций цели совпадают:
.
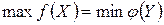Если же в одной задаче функция цели не ограничена, то двойственная ей задача не имеет планов.
Теорема 5.3 (теорема о равновесии). Если оптимальное решение задачи обращает какое-то ее ограничение в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю. Если же какая-то компонента оптимального плана положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в строгое неравенство.
|
|
|
