Решение двойственной задачи

 

В данном параграфе мы рассмотрим пример решения двойственной задачи, основанный на теореме о равновесии (теорема 5.3).

Пример 4.2. 1. Решить общую задачу линейного программирования.
2. Составить и решить двойственную задачу, используя теорему о равновесии.

 

z (X) = – 5 x ₁ + 3 x ₂ + 5 x ₃ – 7 x ₄ ® max, (4.15)

2 x ₁ + x ₂ + x ₃ + 3 x ₄ ³ – 3,

2 x ₁ + 3 x ₂ + 4 x ₃ + 2 x ₄ £ 3, (4.16)

– x ₁ + 2 x ₂ + 2 x ₃ – x ₄ = 4,

x ₂, x ₃, x ₄ ³ 0.

 

Решение. Для удобства составления двойственной задачи и решения основной задачи добьемся того, чтобы все ограничения задачи на максимум были равенствами или неравенствами вида £. Для этого умножим первое неравенство системы (4.16) на – 1. Мы приходим к задаче:

 

z (X) = – 5 x ₁ + 3 x ₂ + 5 x ₃ – 7 x ₄ ® max, (4.17)

– 2 x ₁ – x ₂ – x ₃ – 3 x ₄ £ 3,

2 x ₁ + 3 x ₂ + 4 x ₃ + 2 x ₄ £ 3, (4.18)

– x ₁ + 2 x ₂ + 2 x ₃ – x ₄ = 4,

x ₂, x ₃, x ₄ ³ 0.

 

1. Для решения задачи (4.17) – (4.18) методом Штифеля введем в первое и во второе ограничения системы (4.18) добавочные переменные y ₁³ 0 и y ₂³ 0.

y ₁ = 2 x ₁ + x ₂ + x ₃ + 3 x ₄ + 3,

y ₂ = – 2 x ₁ – 3 x ₂ – 4 x ₃ – 2 x ₄ + 3, (4.19)

0 = x ₁ – 2 x ₂ – 2 x ₃ + x ₄ + 4,

y ₁, y ₂, x ₂, x ₃, x ₄ ³ 0.

 

Таким образом, задачу (4.17), (4.19) можно записать в виде жордановой таблицы 4.12:

 

 

	– x 1	– x 2	– x 3	– x 4				– x 2	– x 3	– x 4
y 1	–2	–1	–1	–3			y 1	–5	–5	–1	–5
y 2							y 2
	–1			–1			x 1	–2	–2		–4
z		–3	–5				z

Табл. 4.12. Табл. 4.13.

 

Заметим, что числа, составляющие первые три строки таблицы 4.12, совпадают с числами, образующими основную матрицу системы (4.18). Последняя строка таблицы состоит из коэффициентов функции цели (4.18), взятых с противоположным знаком. Таким образом, первоначальная жорданова таблица мола быть составлена сразу из условия исходной задачи (4.17) – (4.18).

На первом шаге метода Штифеля выберем в качестве разрешающего элемента элемент а ₃₁ = – 1. При этом неограниченная на знак свободная переменная x ₁ меняется с базисной переменной 0. После первого шага из таблицы можно вычеркнуть столбец, верхний заглавный элемент которого равен нулю (первый столбец). Строку, соответствующую неограниченной на знак переменной x ₁, можно, предварительно запомнив, исключить из таблицы.

После первого шага мы приходим к таблице 4.13. В крайнем правом столбце таблицы 4.13 имеется отрицательное число а ₁₄ = – 5. Следовательно, базисное решение, соответствующее данной таблице, не является опорным планом задачи (4.17), (4.19). Для того чтобы попытаться войти в область планов задачи, нужно найти в первой строке таблицы 4.13 отрицательное число (например, а ₁₃ = – 1) и выбрать разрешающий элемент в столбце, содержащем данный отрицательный элемент (в данном случае – это третий столбец).

Разрешающий элемент в третьем столбце выбираем по принципу минимального симплексного отношения. В данном случае минимальное симплексное отношение соответствует как раз элементу а ₁₃ = – 1. Дело в том, для второго оставшегося элемента а ₂₃ = 0 симплексное отношение вообще не определено. Выбирая в таблице 4.13 в качестве разрешающего элемента а ₁₃ = – 1, после одного шага метода Штифеля, мы приходим к таблице 4.14:

 

 

	– x 2	– x 3	– y 1		ti 2			– x 2	– x 4	– y 1
x 4			–1				x 3		1/5	–1/5
y 2					11/8		y 2	–1	–8/5	8/5
z	–3	–5					z

Табл. 4.14. Табл. 4.15.

 

Из таблицы 4.14 видно, что соответствующее ей базисное решение уже является опорным планом задачи (т.к. свободные члены b ₁ = 5 и
b ₂ = 11 не являются отрицательными числами). Но наличие отрицательных оценок свободных переменных говорит о том, что данный опорный план не является оптимальным. Сделаем еще один шаг метода Штифеля. Выберем для поиска разрешающего элемента второй столбец, соответствующий наименьшей отрицательной оценке – 5.

Для чисел а ₁₂ = 5 и а ₂₂ = 8 вычислим симплексные отношения и запишем их в правый дополнительный столбец таблицы 4.14:

 

 

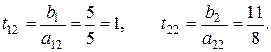
Минимальное симплексное отношение приходится на первую строку. Поэтому в качестве разрешающего элемента нужно выбрать элемент а ₁₂ = 5. После пересчета мы приходим к таблице 4.15. Все оценки свободных переменных в таблице 4.15 строго больше нуля. Следовательно, мы получили оптимальный опорный план, и этот план является единственным.

Некоторые компоненты оптимального плана и добавочные переменные y ₁ и y ₂ находятся из таблицы 4.15.

как свободные переменные.

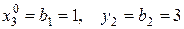– значения базисных переменных.

При этом максимум функции цели находится в правом нижнем углу таблицы:

 

.

 

Значение переменной найдем из запомненной ранее третьей строки таблицы 4.13:

 

.

 

Таким образом, мы нашли решение исходной задачи (4.15) – (4.16):

 

.

 

2. Составим задачу, двойственную к исходной задаче (4.17) – (4.18). Мы получим следующую задачу на минимум:

 

g (Y) = 3 y ₁ + 3 y ₂ + 4 y ₃ ® min, (4.20)

– 2 y ₁ + 2 y ₂ – y ₃ = – 5,

– y ₁ + 3 y ₂ + 2 y ₃ ³ 3,

– y ₁ + 4 y ₂ + 2 y ₃ ³ 5, (4.21)

– 3 y ₁ + 2 y ₂ – y ₃ ³ – 7,

y ₁, y ₂ ³ 0.

 

Обозначим через – оптимальный опорный план двойственной задачи (4.20) – (4.21) воспользуемся теоремой о равновесии.

1. Подставим координаты оптимального опорного плана в систему ограничений (4.18):

Так как второе ограничение превратилось в строгое неравенство, то соответствующая компонента оптимального опорного плана двойственной задачи равна нулю (). Осталось найти компоненты и . Для этого воспользуемся второй частью теоремы о равновесии.

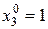2. Так как третья компонента оптимального опорного плана строго больше нуля (), то соответствующее (третье) ограничение двойственной задачи, при подстановке в него компонент оптимального плана , обратится в равенство. Данное равенство вместе с первым ограничением (которое само по себе является равенством) дают нам систему линейных уравнений для нахождения и :

 

(4.22)

Подставляя в систему (4.22) уже найденное значение , получим систему двух уравнений с двумя неизвестными:

(4.23)

Решением данной системы является . Таким образом, мы нашли оптимальный опорный план двойственной задачи: . При этом экстремальные значения функций цели взаимно-двойственных задач совпадают:

.

ПРИЛОЖЕНИЯ

 

Контрольное задание №1. Вычислить ранг матрицы.

 

1. 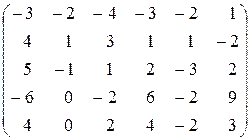.	2. .
3. .	4. .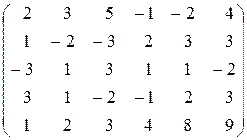
5. .	6. .
7. .	8. .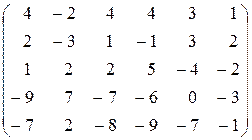
9. 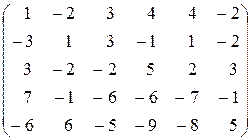.	10. .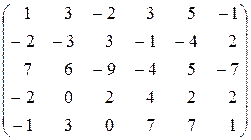
11. 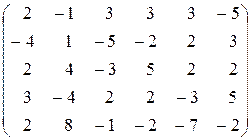.	12. .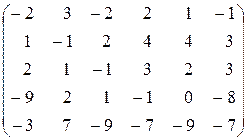
13. .	14. .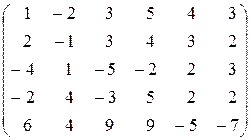
15. .	16. .
17. 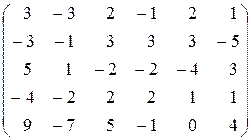.	18. .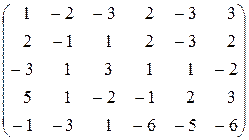
19. .	20. .

 

 

Контрольное задание №2. Найти общее решение системы линейных уравнений.

 

 

1.	2.
3.	4.
5.	6.
7.	8.
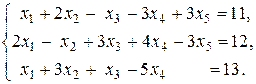
9.	10.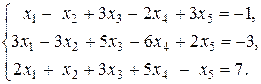
11.	12.
13.	14.
15.	16.
17.
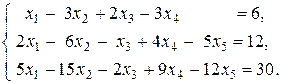
18.	19.

 

Контрольное задание №3. Дана общая задача линейного программирования. Требуется: 1) решить задачу методом Штифеля; 2) составить и решить двойственную задачу, используя теорему о равновесии.

 

 

 

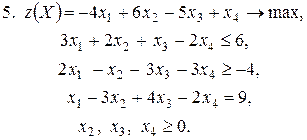
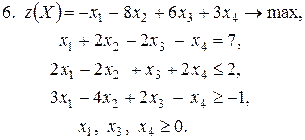
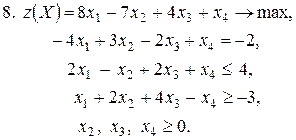
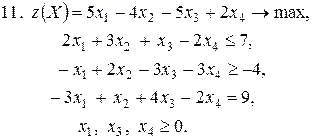
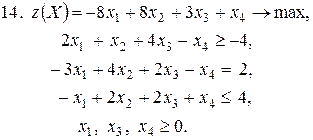
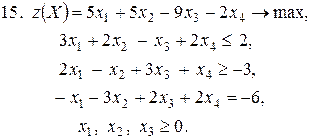
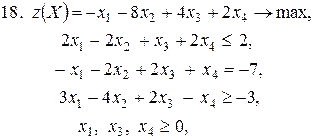
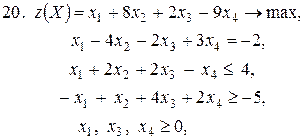
ЛИТЕРАТУРА

 

Основная

 

1. Замбицкий Д.К. Линейная алгебра и линейное программирование: Учеб. пособие / Д.К. Замбицкий, М.К. Замбицкий. – Кишинэу: Еврика, 1997. – 200 с.

2. Зуховицкий С. И. Линейное и нелинейное программирование / С. И. Зуховицкий, Л.И. Авдеева. – М.: Наука, 1967. – 352 с.

3. Полунин И.Ф. Курс математического программирования / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

4. Полунин И.Ф. Курс математического программирования: Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва», «Бухгалтерский учет в сельском хоз-ве» и «Экономика и организация водного хоз-ва» / И.Ф. Полунин. – 3-е изд., доп. – Минск: Вышэйш. шк., 1975. –
380 с.

5. Полунин И.Ф. Курс математического программирования: Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва» и «Бухгалтерский учет в сельском хоз-ве» / И.Ф. Полунин. – Минск: Вышэйш. шк., 1970. – 318 с.

 

Дополнительная

 

1. Зуховицкий С. И. Линейное и выпуклое программирование / С.И. Зуховицкий, Л.И. Авдеева. – 2-е, изд. переработ. и доп. – М.: Наука, 1967. – 360 с.

2. Полунин И.Ф. Математическое программирование в землеустройстве: Учеб. пособие для землеустроит. фак. с.-х. вузов / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

3. Еремин И.И. Теория линейной оптимизации / И.И. Еремин; Отв. ред. Л.Д. Попов; РАН. УРО. Ин-т математики и механики. – Екатеринбург, 1999. – 312 с.

 

Составитель ст. преп. Уксусов Сергей Николаевич

Редактор Тихомирова О.А.

 

 

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: