Понятие математической структуры

 

Опр1 Пусть даны некоторые множества М₁,…,М_n. Всякое подмножество DÌМ₁×…×М_n называется отношением определенным на множествах М₁,…,М_n, при этом говорят, что (m₁,m₂,…,m_n),m_iÎМ_i находится в отношении D, если (m₁,…,m_n)ÎD.

В курсе алгебры вы изучали Бинарные, n-арные, унарные oтношения, операции, если М₁=…=М_n, отображения их вы определили через отношения.

Ясно, что если на множествах М₁,…, М_n рассмотрим два разных подмножества D₁ и D₂,то свойства отношений будут чем-то отличаться и мощность множества всех отношений равна Р (М₁× …×М_n)

Ясно, что если хотя бы одно из множеств М_i бесконечно, то и множество отношений будет бесконечным. Поэтому бессмысленно изучать все отношения существующие на данной системе множеств. Здесь математика идет другим путем, а именно сначала выделяют отношения с наперед заданными свойствами, а за тем изучают множества, на которых они заданы или ищут те множества, на которых эти отношения выполняются.

Возьмем конечную систему различных множеств.E_,F и G пусть их три. Пусть D₁,…,D_к - некоторые отношения на системе множеств Е, F,G. Причем мы их не будем явно фиксировать, а лишь потребуем, чтобы они обладали заданными свойствами.

(1) А₁,…, А_t.

Эту совокупность отношений обозначим s ={D₁,…, D_k}. Может случиться, что таких систем будет не одна, а несколько

ПРИМЕР: D(а,в)=D(в,а) на R, по “*”,”+”.

Обозначим через Т множество всех систем отношений s обладающих свойствами (1).

Опр2 Если Т¹Æ, то говорят, что элемент sÎТ определяет на множествах E, F, G математическую структуру рода Т. Ясно сформулированные свойства А₁,…,А_t, определяющие множество Т называется аксиомами структур рода Т, а множества E,F,G- базой структур рода Т.

ЗАМЕЧАНИЕ 1:Всем структурам одного и того же рода дается специальное название: структура группы, структура векторного пространства, структура евклидова пространства, структура кольца.

ЗАМЕЧАНИЕ 2: Если база состоит из нескольких множеств, то иногда одно из них играет основную роль, а остальные вспомогательную в определенных структурах, тогда говорят, что эти структуры определены на множестве Е., Например: Е, V_n+1, поле K- модель проективной плоскости над полем К или векторное пространство над полем К (о векторном пространстве).

ПРИМЕР 1: Структура группы: База 1- множество, 1-отношение, уд-ее 4 аксиомам.

ПРИМЕР 2: Структура евклидова пространства по Гильберту (отношения: инцидентность, порядок, равенства,……….).

ПРИМЕР 3: Структура Афф. Пространства по Вейлю.

ПРИМЕР 4: Евклидово пространство над векторным пространством V.

Систему аксиом будем обозначать å

Опр3 Теория структур рода Т-это множество Á(å) предложений (теорем), каждое из которых выводимо из аксиом системы å, определяющих структуру рода Т.

Математика занимается построением теорий структур заданного рода Т. Метод - аксиоматический.

 

Интерпретация системы аксиом

Не на всяком множестве Е можно определить структуру любого рода. Например, на конечном множестве Е можно определить структуру n-мерного векторного пространства над бесконечным полем. Но ту же структуру можно определить на множестве К×К×…×К=Кⁿ

Мы уже говорили о структурах и базах, и в определении структуры звучало: если Т¹Æ. Но когда же оно может быть пусто?

a) Данная база не допускает структуру требуемого рода. Тут простор для раздумий …$ др. база.

b) Не существует базы, допускающей требуемую структуру (т.е. всегда Т=Æ)

Опр1 Система аксиом å={A₁, …, At}, определяющая структуру рода Т называется содержательно не противоречивый, если существует база, допускающая требуемую структуру. Если такой базы не существует, то å называется противоречивой.

Опр2 Если указано конкретное множество М, на котором можно придать конкретный смысл отношениям D_1, D₂,..., D_к, так, что все аксиомы А₁, А₂,..., А_t оказываются выполненными, то, говорят, что построена интерпретация системы аксиом å, а само множество М называют моделью структур рода Т.

ПРИМЕР: Проективное пространство. Аффинное пространство на множестве Е, множество матриц 1×n.

Следовательно, чтобы доказать непротиворечивость (содержательную) системы аксиом å={A₁,..., A_t}, достаточно построить хотя бы одну ее интерпретацию.

 

Изоморфизм структур

Пусть система аксиом å={A₁,..., A_t} содержательно непротиворечива и, следовательно, определяет структуры рода Т с основными отношениями D₁, D₂,..., D_к.

Пусть на множестве М^/ опеделена структура s^/ÎТ, а на множестве М^// определена структура s^//ÎТ. Это означает, что мы придали конкретный смысл отношения D_i, i=1,...,k, на множествах М^/ и М^//. Обозначим их D_i^/ и D_i^// соответственно.

Опр1 Структуры s^/ и s^// называется изоморфными, если существует биекция f:M^/®M^//, такая, что элементы х^/,у^/, v^/ÎM^/ находятся в отношении D^/_i, тогда и только тогда, когда элементы f (х^/), f (у^/), f (v^/)ÎМ^// находится в отношении D_i^//. Само отображение f называется изоморфизмом структур s^/ и s^//.

Опр2 Изоморфизм множества М со структурой s на себя называется автоморфизм множества М с данной структурой (автоморфизм группы, кольца и т.д.)

ЗАМЕЧАНИЕ:

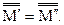
Пример:f: R⁺ ® R: f(x)=lnx.

Какой должна быть система аксиом?

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: