Аксиомы Вейля трехмерного евклидова пространства

W1 "AÎЕ, " ÎV существует одна и только одна точка Х, т.что = .

W2 "А, В, СÎЕ выполняется равенство + = .

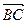W3 Множество G есть множество положительно определенных билинейных форм, таких, что, если g(, )ÎG, то G = {lg}, lÎR₊, т.е. в пространстве V задано положительно определенная билинейная форма с точностью до положительного множителя.

Напомним: положительная определенность означает, что g(, )>0, если ¹ (можно потребовать симметричность) и т.п.

W1, W2 определяют структуру трехмерного вещественного аффинного пространства.

Здесь мы исходим из того, что структура V и структура R нам известны. Поэтому структура Е₃ (по Вейлю) определена лишь тремя аксиомами.

Имеет место

Теорема 1 Система аксиом Вейля непротиворечива, если непротиворечива арифметика действительных чисел.

ДОКАЗАТЕЛЬСТВО: Построим интерпретацию. В качестве V возьмем множество столбцов вида , где а₁,а₂, а₃ - произвольные действительные числа. Сумма векторов и умножение вектора на число определяются естественным образом

+ = , α = , =

Мы знаем, что множество таких столбцов, образуют трехмерное векторное пространство. Множество G определяют так: Рассмотрим билинейную форму g₀(, ) = x₁y₁+x₂y₂+x₃y₃ и положим G={lg₀}, где l>0. Ясно, что для любых форм g₁,g₂ÎG имеет место W3: g₁=l₁g₀, g₂=l₂g₀ Þ g₁= g₂

Т.е. они отличаются лишь постоянным множителем. Теперь самое главное - это множество Е. Точкой назовем любую строку вида (m₁,m₂,m₃), m_1,m₂,m₃Î R.

(1) s ((m₁,m₂,m₃),(n₁,n_2,n₃)) =

Проверим W1 Пусть А=(а₁,а₂, а₃) произвольная точка, = - вектор. Ясно, что $! Х=(x₁,x₂,x₃): x₁ - a₁ = p₁, x₂ - a₂ = p₂, x₃ - a₃ = p₃.

W2. Пусть А=(а₁,а₂,а₃), В=(в₁,в₂,в₃) и С=(с₁,с₂,с₃) легко проверить, что + 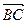= , расписав все это по (1) в₁ - а₁+с₁ - в₁ = с₁ - а₁.

Мы построили интерпретацию. Значит система аксиом å_w- непротиворечива.

Имеет место

Теорема 2 Система аксиом Вейля трехмерного евклидова пространства - категорична.

(сказать идею)

 

СЛЕДСТВИЕ: Система аксиом Вейля- полна

 

§10 Эквивалентность аксиоматик å_W и å_H (Вейля и Гильберта)

 

В этом параграфе мы докажем эквивалентность аксиоматик Гильберта и Вейля. Сначала докажем, что в теории Á(W) можно получить все аксиомы å_Н как теоремы. Но прежде, надо в теории Á(W) построить все основные понятия теории Á(Н). Вообще говоря, мы это уже делали на втором курсе.

Напомним: Пусть L_k, k=1, 2 одномерное или двумерное подпространство векторного пространства V. Введем на множестве всех точек пространства Е₃ бинарное отношение D. Пусть А, ВÎЕ, АDВÛ ÎL_k. Мы доказывали, что D - отношение эквивалентности элемент _, при к=1 называли прямой, а при к=2 называли плоскостью. L_k называли направляющим подпространством прямой или плоскости.

Таким образом, прямая однозначно определяется заданием одной точки и подпространства L₁ или, что то же самое, одного вектора из L₁. Плоскость однозначно определяется заданием точки и L₂ (или его базиса, состоящего из двух линейно независимых векторов , Î L₂). Прямую или плоскость с направляющим подпространством L будем обозначать (А, L).

Вспомним, как в Е₃, вводится система координат: выберем т. ОÎЕ и базис в V , , ; упорядоченная тройка объектов (О ) – система координат.

По W1 $ А, В, и С: = , = , = . Ясно, что т О, А и В не лежат на одной прямой, т. к. векторы и линейно независимы и не принадлежат одному и тому же одномерному направляющему подпространству. А точки О, А, В и С не лежат в одной плоскости (самостоятельно). Значит I₃ и I₈ выполняется.

I₁ и I₂: Через любые две точки А и В проходит единственная прямая.

Док-во. Рассмотрим прямую d: (А, ). Вектор и будет определять L₁ ($ доказано I₁)

Пусть $d^/: (А, L^/₁) или (В, L^/₁), но это означает, что Î L^/₁Þ L₁=L₁^/ и, значит, d и d^/ совпадают.

I₄ и I₅: Через любые три строчки А,В, и С, не лежащие на одной прямой, проходит единственная плоскость.

Идея: плоскость s определяется т. А и подпространством L натянутым на и . Пусть s^/ проходит через эти же три точки. Но пара точек по W1 определяет единственный вектор в V, т.е. снова приходим к векторам и , а ÞL и L^/ совпадают Þ s = s^/.

I₆: Если точки А и В прямой d лежат в плоскости s, то и все точки прямой d лежат в s (самостоятельно).

I₇ (более сильное докажем): Если две плоскости s и s^/ имеют общую точку А, то они имеют общую прямую, которой принадлежат все общие точки плоскостей s и s^/.

Идея: пусть s = (А,L₂), s^/ = (А,L^/₂), но L₂ и L₂^/- различны. DimL₂+dimL₂^/= 4>3, значит не пересекаться они не могут значит dim(L₁ÇL₂)=1, причем L1ÇL₂ÌL₁ и L₁ÇL₂ÌL₂.

Все с H_I!

У нас уже промелькнули слова о пересечении подпространств. Поэтому докажем в Á(W) H_V. Чтобы ввести понятия, участвующие в H_V придется потрудиться.

Лемма: Если две прямые лежат в одной плоскости и их направляющие подпространства не совпадают, то эти прямые пересекаются.

Доказательство: Пусть (А, ) и (В, ) прямые лежащие в данной плоскости s. Векторы и - линейно независимы по условию. Значит, образуют базис напр. подпространства L₂ плоскости s.Следовательно, =a +b . По W1 $ М и М^/, т. что = a ÎL₁()ÞMÎ(А, ); =(-b) ÎL₁() ÞM^/Î(В, ). Тогда имеем = - Þ = + = ^/. По W1 М=М^/. Значит прямые пересекаются.

Ч.т.д.

ЗАМЕЧАНИЕ: Кстати только по одной точке, учитывая H_I1,2 .

Опр. 1 Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

Пусть две различные прямые (А, L₁) и (В, L₁) имеют одно и то же направляющее подпространство L_1. По df прямой это элементы фактор множества , где D определяется подпространством L_1. А классы эквивалентности, как известно, не пересекаются.

Кроме того, они, очевидно, лежат в одной плоскости определяемой т. А и векторами и ÎL. Учитывая лемму, получили следующий признак // прямых.

Теорема1. Две различные прямые параллельны тогда и только тогда, когда они имеют общее направляющее подпространство и не имеют общих точек.

H_V: Через данную т. А, не лежащую на данной прямой d, проходит одна и только одна прямая, // прямой d.

Доказательство. Существование очевидно, т.к. L- направляющее подпространство d, то прямая (A, L) // d по теореме 1. Единственность: пусть существует еще одна прямая (A, L^/) // d. Но тогда по той же теореме1 L = L^/. Значит прямые (A, L) и (A, L^/) – совпадают, по определению прямой.

Аналогично можно ввести понятие и доказать соответствующие свойства для // плоскостей.

Перейдем к доказательству H_II. Для этого нам понадобится построить в Á(W) отношение лежать между, и убедиться, что оно обладает свойствами H_II. Построим так: сначала введем понятие луча, заодно и угла. А потом докажем все H_II и введем понятие отрезка.

Поехали: Пусть d- прямая, L₁ - ее направляющее подпространство. Рассмотрим множество W= L₁\{ } и на этом множестве введем отношение сонаправленности ­­: ­­ Û$l>0: =l

Нетрудно доказать, что это отношение является отношением эквивалентности (сами). Заметим, что состоит из двух элементов. Для доказательства возьмем вектор ÎW и = - . К и К не совпадают. Любой вектор ÎW можно представить виде =m , m¹. Если m>0, то ÎК ,а если m<0,то =½m½ Þ ÎК _.

Опр 3 Каждый из элементов фактор множества будем называть направлением на прямой d. Если векторы и принадлежит противоположным направлениям данной прямой, то будем говорить, что они противоположно направлены: ­¯ .

Таким образом, на каждой прямой имеется только два направления.

ЛЕММА: Если ­­ , то + ­­ и + ­­ .

Доказательство: =l Þl + =(l+1) ­­ ­­ .

Опр 4. Пусть d произвольная прямая, О- некоторая ее точка, а W₀- одно из направлений на этой прямой. Множество h всех точек М, т. что ÎW_0, называется лучом, исходящим из т.О. Направление W₀ называется направлением этого луча.

Поскольку на прямой имеются только два направления, то существует два и только два луча прямой d, исходящие из произвольной точки прямой. Эти лучи называются дополнительными. Ясно, что если h и h^/. Дополнительные лучи прямой d, то множество точек прямой {M÷MÎd}=hÈh^/ÈО.

Опр 5. Углом называется фигура, состоящая из т. О и двух лучей h и k, исходящих из этой точки. Угол называется развернутым, если h и k- дополнительные лучи.

Опр 6. Будем говорить, что точка М лежит между точкой А и точкой В, если ­­ .

А теперь несложно будет доказать II₁, II₂ и II₃. И даже более сильное утверждение, что из трех точек прямой одна и только одна лежит между двумя другими.

Теперь докажем аксиому Паша. Но для этого нам понадобятся координаты на плоскости. Ее направляющее подпространство L₂. Если , его базис, то О - система координат на плоскости. М (х, у) Û = х +у . Далее, если А (х₁,у₁) и В (х₂,у₂), то = (х₂-х₁,у₂-у₁). Имеет место хорошо известное вам утверждение.

Утверждение 1. т. М (х, у) лежит между двумя точками А (х₁,у₁) и В (х₂,у₂) тогда и только тогда, когда $l>0, так что

x = , y=

Следствие: $ бесконечное множество точек, лежащих между т. А и В. Т.к. теперь при фикс. х₁ и х₂ и любом l>0, х и у определены. И только теперь:

Опр 7. Множество, состоящее из двух точек А и В и всех точек, лежащих между ними, называется отрезком и обозначается АВ или ВА.

Докажем аксиому Паша.

Теорема Паша. Пусть А, В и С- три точки, а d – прямая, лежащая с данными точками в одной плоскости и не проходящая через них. Если прямая d пересекает отрезок АВ, то она пересекает, в точности один из отрезков ВС или АС.

Доказательство: Выберем систему координат О так, чтобы ОÎd и ÎL_d1, т. е. //d_1.

Пусть в этой системе координат А (х₁,у₁), В (х₂,у₂), С (х₃,у₃). Эти точки не лежат на d, Þ у₁¹0, у₂¹0, у₃¹0. Пусть М (х, у) = dÇAB.

 

$l>0: х = , у = , т.к. MÎd Þ y=0Þy₁+ly₂=0, понятно, что у₁ и у₂ имеют разные знаки, а значит либо у₁у₃ <0, либо у₂у₃<0. Нетрудно доказать, что в первом случае d пересекает АС, а во втором - ВС (сами), что согласуется с имеющимся у нас понятиями о знаках координат и четвертях.

C H_II покончено.

Перейдем к доказательству H_{III .} Мы введем основные понятия и наброски некоторых доказательств.

Опр 7. Отрезки АВ и СД называется равными (АВ=СД), если для любой билинейной формы gÎG выполняется равенство

(*) g(, )=g(, ).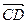

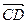Замечание 1. Поскольку в G формы связаны соотношением g₁=lg_2,то если найдется хотя бы одна удовлетворяющая (*), то (*) будет верна и для всех форм из G, т.е. АВ=СД

Замечание2. Т.к. =- , 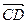=- , а форма билинейна и положительно определена, то понятия равенства отрезков АВ и СД не зависит от порядка, в котором заданы их концы: g(, )=g(- ,- )=-g(,- )=g(, )

Нетрудно проверить выполнениеIII₁, III₂, III₃.

III₂ очевидна (АВ=А^/В^/ÙАВ=А^//ÞА^/В^/=А^//В^//)

III₁ Пусть АВ-некоторый отрезок, а h^/– произвольный луч, с началом А^/. Тогда существует одна и только одна т В^/Îh^/, т. что АВ=А^/В^/

Доказательство: Пусть один из векторов, определяющих направление луча h^/, тогда "M^/Îh^/ $x>0: =x , x>0. Нo =AB Û g(, ) = =g(, )>0 = x²g(, )>0 Þ существует единственное x>0. По W1Þ$! В^/: АВ=А^/В.

III₃. Если А-В-С, А^/-В^/-С^/, АВ=А^/В^/ и В^/С^/, то АС=А^/С^/.Доказывается, используя отношения «лежать между» и положительную определенность формы gÎG.

Опр 8. Ненулевые векторы и называются ортогональными, если они сопряжены относительно любой билинейной формы gÎG, т.е. "gÎG g(, )=0.

Т.к. любые две формы из G связаны соотношением g₁=lg₂, l>0, то если и сопряжены относительно хотя бы одной формы из G, то они сопряжены относительно любой формы из G и, значит, ортогональны.

Опр 9. Две прямые называется ^, если их подпространства ортогональны. Аналогично прямая d^a: L_d ортогонально L_a. И можно ввести понятия ^ плоскостей. (Через двугранный угол или через нормали). Заметим, что подпространства двух ^ плоскостей не ортогональны!

Условие аксиомы W₃, может показаться странным, там ведь множитель l, что означает выбор l?

Оказывается выбор единичного отрезка, соответствует выбору той или иной формы из G. А введение понятия единичного отрезка уже позволяет в Á(W) построить теорию измерений. Выберем произвольный отрезок АВ и назовем его единичным.

Лемма (важная): Если выбран отрезок АВ, то в множестве G $!,билинейная форма gÎG: g(, )=1. (Этот отрезок и назовем единичным).

Доказательство. Очевидно: если g^/ÎG и g^/(, )=m, то форма g= g^/ искомая, если же $ еще одна такая форма, то g₁=lg=l g^/ (, )=1Þl=1Þg₁=g/.

Ч.т.д.

Опр 10. Если АВ - единичный отрезок, то билинейную форму gÎG, т.что g(, )=1 будем называть соответствующей единичному отрезку АВ.

Таким образом, если в Е₃ мы выберем единичный отрезок, то векторное пространство V станет евклидовым векторным пространством (одна форма) и в нем вводится скалярное произведение векторов, и норма вектора :÷ ÷= . Теперь легко в V ввести понятия единичного вектора, ортонормированного базиса, а в Е₃ понятие длины.

Опр 11. Длиной отрезка РQ при выбранном единичном отрезке АВ называется норма вектора : ÷PQ÷= (2).

Имеют место следующие свойства длин отрезков

Свойство 1. Если два отрезка равны, то их длины равны (по формуле (2)).

Свойство 2. Если А-В-С, то êАВê+êВСê=êАСê.

Доказательство. =l 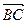, тоêАВê=lêВСê, l>0, т. к. = + 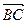, то = (1+l) 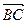ÞêАСê=(1+l) êВСê êАС ê=êВСê+lêВСê=êВСê+ êАВê.

Свойство 3. Длина единичного отрезка равна 1.

Свойство 4. " А,В и СÎ Е₃ ÷АС÷£÷АВ÷+÷ВС÷, причем равенство имеет место тогда и только тогда, когда А-В-С.

Опр 12. Расстоянием между точками А и В называется длина отрезка АВ. Для доказательства III₄ и III₅ вводится понятие движения.

Опр 13. Преобразование Е₃ называется движением, если оно сохраняет расстояния между точками.

И тут уже вступает в силу обычная теория движения евклидовых пространств по схеме Вейля, т. Е. Через параллельные переносны и ортогональные матрицы х^/=А + , где А - ортогональная матрица (А^тА=1).

Имеет место

Теорема (о флагах). Пусть (О,h,a) и (О^/,h^/,a^/)- произвольные флаги. Тогда $! Движение, которое флаг (О,h,a) переводит в (О^/, h^/,a^/).

Опр 14. Две фигуры F и F^/ называются равными, если $ движение, которое одну фигуру переводит в другую.

Ясно теперь, как ввести равенство углов, это соответствует и равенству отрезков веденному ранее. III₄ и III₅ понятно (т.к. полуплоскость в полуплоскости, флаг в флаге ч.т.д.) I

Опр 15. Ðhk=Ðh^/k^/, если существует движение, которое Ðhk переводит в Ðh^/k^/.

III₄. Пусть Ðhk- неразвернутый угол, а (О^/,h^/,a^/)- некоторый флаг. Тогда в полуплоскости a^/ $! луч k^/, исходящая из т.О^/, такой, что Ðhk=Ðh^/k^/.

Доказательство. Пусть О - вершина угла hk, и (O,h,a)-флаг в котором лежит луч k. $! движение f: (О, h, a) ® (О^/, h^/, a^/) и k^/=f(k). k^/ - искомый.

!: Пусть k^//: Ðhk=Ðh^/k^//Þ$ движение f^/,такое что f ^/(h)=h^/ и f ^/(k)=k^// , но тогда f^/:(O,h,a)®(O^/,h^/,a^/)Þk^/=k^//.

Вместо III₅ докажем более сильное утверждение.

Теорема (Iпризнак равенства треугольников). Если в DАВС и DА^/В^/С^/ АВ=А^/В^/, АС=А^/С^/ и ÐА=ÐА^/, то DАВС=DА^/В^/С^/.

Доказательство. Т.к. ÐА=ÐА^/, то $ движение ¦, т. что [АВ)®[А^/В^/), а луч АС в луч А^/С^/. Пусть f(B)=B^//, f(C)=C^//, тогда АВ=А^/В^// и по условию АВ=А^/В^/. В силу III₁ и транзитивности В^/=В^//. Аналогично С^/=С^//. Следовательно DАВС ® DА^/В^/С^/ Þ DАВС=DА^/В^/С^/.

H_IV. Ведем единичный отрезок и понятие числовой оси и т.п. Так как V над R, то можно установить взаимно - однозначное соответствие между R и точками прямой по W1.

А значит будут выполнены аксиомы Архимеда и Кантора.

Таким образом, в теорий Á(W) выполняет все å_H

Обратное: Мы говорили о том, что в Á(H) можно ввести координаты, ^, направление, луч, вектор, а, следовательно, будут иметь место все å_W.

Итак, мы доказали две важные теоремы:

Теорема I. С истемы аксиом å_H и å_W эквивалентны.

Теорема II. Система аксиом å_H непротиворечива, если непротиворечива арифметика действительных чисел.

P.S. В Ефимове прямо построена аналитическая модель для å_H.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: