Требования, предъявляемые к системам аксиом

Опр1 Систему аксиом называют внутренне непротиворечивой, если из нее нельзя получить логическим путем два утверждения, из которых одно является отрицанием другого.

Вопрос о внутренней непротиворечивости данной системы аксиом, сводится к вопросу техники логических выводов из этих аксиом. Т.е. к правилам построения новых предложений из уже имеющихся. Этим как раз и занимается математическая логика. Заметим, однако, что если мы установили содержательную непротиворечивость системы аксиом å, т.е. построили ее интерпретацию, то ясно, что из å нельзя вывести А Ù . Т.к. этим свойствам должно удовлетворять некоторое отношение D_i из тех, которые определяют структуру Т, но никакое отношение, по определению, не может обладать свойствами А и одновременно. Значит, если построена интерпретация, то в теории Á(å) с логикой все в порядке и вопрос о внутренней непротиворечивости сводится к вопросу о внутренней непротиворечивости тех понятий, при помощи которых построена данная интерпретация. Если же эта система понятий внутренне непротиворечива, то доказав содержательную непротиворечивость системы аксиом å, мы тем самым докажем и ее внутреннюю непротиворечивость.

Значит, при построении интерпретации мы должны использовать достаточно надежные понятия, относительно которых у нас есть хоть какая-то уверенность, что их система внутренне непротиворечива.

Таким образом, оставаясь только в рамках геометрии, мы можем решать вопрос лишь о содержательной непротиворечивости данной системы аксиом, а не внутренней.

Как правило, при построении моделей систем аксиом, определяющих структуры, изучаемые в геометрии, мы используем различные числовые множества. Поэтому, в лучшем случае, мы можем получить высказывание типа: “Система аксиом å непротиворечива, если непротиворечива вещ. (целая и т.д.) арифметика”

Непротиворечивость целой арифметики не доказана, вещественной тоже. С теорией множества есть свои сложности (континуум- гипотеза)…

Итак, первым важнейшим требованием к системе аксиом является ее непротиворечивость.

Второе требование независимость. Вот, что под этим подразумевается. Пусть å непротиворечива и, значит, можно строить теорию Á(å) структур рода Т. Возникает вопрос, тот который стоял перед геометрами, изучавшими V постулат Евклида. Все ли аксиомы системы å необходимы для определения данного рода структур, т.е. нельзя ли уменьшить число этих аксиом, не меняя Т?

Опр. 2 Пусть АÎå. Она называется зависимой от остальных аксиом системы å, если предложение А является логическим следствием из остальных аксиом системы å. Если в å такого предложения нет, то система аксиом å называется независимой.

Как же выяснить, является ли данная система аксиом независимой или нет?

Пусть А зависима от остальных аксиом системы å. Рассмотрим систему å^/=å\{A}. Ясно, что å^/ определяет то же множество отношений, т.е. структуру того же рода что и å, и всякая интерпретация å будет являться интерпретацией системы å^/, т.к. в å^/ меньше аксиом. Рассмотрим систему å^*=å^/È{ }. Т.к. å^/Ìå^*, то всякая интерпретация å^* есть интерпретация å^/, а значит, если А зависима, то в ней должна выполнятся А., Но это означает, что å^* противоречива. Т.е. если мы построим интерпретацию å^*, то А не является зависимой от остальных. И если теперь для каждой аксиомы из å мы построим соответствующую å^* и ее интерпретацию, то å- независима.

ПРИМЕР1: Конечная проективная плоскость Р.

Р₁: Для любых двух различных точек А и В $ и притом единственная прямая, инцидентная каждой из этих точек.

Р₂: Существует четыре точки, из которых никакие 3 не инцидентны одной прямой.

Р₃: Для любых двух прямых существует точка, инцидентная каждой из этих прямых.

1.Непротиворечивость. Е={A,B,C,M,N,P,O}. F-стороны, медианы и окружность.

 

В

 

 

M N

 

 

	А

A C

	P

 

2. Независимость. а) 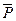₁ÈR₂ÈR_{3 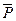1}:$ различные точки А и В, через которые не проходит прямая: Е^*=Е то же самое, Р^*=Р\СМ.

б)R₁È 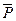₂ÈР₃: Е^**={A,B,C,} F^**-стороны (точек всего 3)

B

C

B

 

 

		C		А		D
	A

 

в) Р₁ÈР₂È 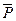₃ : Е₁={A,B,C,D, F₁={стороны и диагонали}. Независимость Р - доказана.

ПРИМЕР 2: Г и Л –(V постулат и V^*)

Трудно говорить о независимости. Иногда å бывает построена так, что вопрос о независимости ставить бессмысленно. Например, нельзя говорить о независимости аксиомы Паша, т.к. для формулировки аксиомы конгруэнтности мы должны иметь понятия луча и полуплоскости, а они вводятся на основании аксиомы Паша.

 

Следующее требование – полнота. Трудный вопрос. А, может, переставляя аксиомы, т.е. в терминах теории Á(å), мы сформулируем такое предложение, которое ни доказать, ни опровергнуть в данной теории нельзя? Рассмотрим непротиворечивую систему аксиом å.

Опр3 Система аксиомам å называется дедуктивной неполной или просто неполной, если $ предложение А т. что

a) А сформулировано в терминах теорий Á(å) и, следовательно, не вводит новых отношений

b) А не зависит от аксиом системы å

c) Система аксиом åÈ{A} непротиворечива.

Если такого предложения в Á(S) нет, то å называется дедуктивно полной.

И снова проведем рассуждение, которое позволит нам получить некий план действий для проверки полноты.

Пусть å- неполная и, значит, $ утверждение А, удовлетворяющее Опр3. Из с) следует, что å^/=åÈ{А}-непротиворечива, и А не зависит от å, следовательно, непротиворечива и å^*=åÈ{ }. Пусть М^/ и М^* - их соответствующие модели, ноåÌå^/ и åÌå^* значит М^/и М^* есть модели å. Но в М^/ выполняется А, а в М^*- и, значит, М^/ и М^* не изоморфны. Следовательно, если система аксиом å неполная, то существуют ее не изоморфные интерпретации.

Опр4 Система аксиом называется категоричной, если все ее интерпретации изоморфны.

УТВЕРЖДЕНИЕ: Если система аксиом - неполная, то существуют ее неизоморфные интерпретации.

Т.е. из категоричности следует полнота. Но из полноты категоричность не следует и, значит из не категоричности, не следует неполнота.

Докажем, что Р не категорична. F={(1,2,3,11); (4,5,6,11); (7,8,9,11); (1,4,7,13); (2,5,8,13); (3,6,9,13); (1,5,9,12,); (3,4,8,12); (7,2,6,12); (7,5,3,10); (1,8,6,10); (9,4,2,12); (10,11,12,13)}.

E={1,2,3, …,13}. Р_1,Р_2,Р₃- выполняются, но интерпретации не изоморфны.

Опр5 Пусть å непротиворечива и определяет структуру рода Т. Если все модели системы аксиом å изоморфны, то теория Á( å ) называется однозначной. Если же å не категорична, то Á( å ) называется многозначной. Например: теория групп.

Сказать об опровержимости и доказуемости.

И в заключение. Пусть даны две системы аксиом. Могут ли они порождать одну и ту же теорию?

Опр6 Системы аксиом двух теорий называется эквивалентными, если в каждой из этих теорий можно построить основные понятия другой теорий так, что все аксиомы одной теории будут теоремами в другой теории.

На следующей лекции мы этим и займемся.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: