 |
Равносильные логические выражения
|
|
|
|
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения 
равносильны.
Построим сначала таблицу истинности логического выражения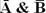 
(таблица 9).
Таблица 9 – Таблица истинности логического выражения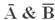 
| А | В | 
| 
| 
|
Теперь построим таблицу истинности логического выражения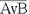 
(таблица 10).
Таблица 10 – Таблица истинности логического выражения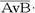 
| А | В | А v В |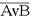 
|
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
= 
.
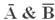Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1
1. Составим таблицу истинности для формулы, которая содержит две переменные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
|
|
|
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения:
D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С)
количество столбцов (таблица 12):
1) А,
2) В,
3) С,
4) не A – это инверсия А (обозначим Е),
5) B + C – это операция дизъюнкции (обозначим F),
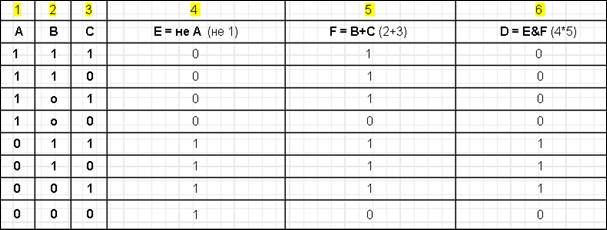
6) D = неA & (B+C), т.е. D = E & F – это операция конъюнкции.
Таблица 12 – Таблица истинности логического выражения D = неA & (B+C)
Логические функции
Любое составное высказывание можно рассматривать как логическую функцию F(Xp Xv..., Хп), аргументами которой являются логические переменные Xv Xv..., Хп (простые высказывания). Функция и аргументы могут принимать только два различных значения; «истина» (1) и «ложь» (0).
Выше были рассмотрены функции двух аргументов: логическое умножение F(A,B) = А & В, логическое сложение F(A,B) = AvB, а также логическое отрицание F(A ) = Ā, в котором значение второго аргумента можно считать равным нулю.
Каждая логическая функция двух аргументов имеет четыре возможных набора значений аргументов. По формуле мы можем определить, какое количество различных логических функций двух аргументов может существовать:
N = 24 = 16
Таким образом, существует 16 различных логических функций двух аргументов, каждая из которых задаётся своей таблицей истинности (таблица 13).
Таблица 13 – Таблицы истинности логических функций двух аргументов
| Аргумент | Логическая функция | ||||||||||||||||
| A | B | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
Легко заметить, что здесь логическая функция F2 являеттся функцией логического умножения, F8 — функцией логического сложения, F13 — функцией логического отрицания для аргумента А и F11 — функцией логического отрицания для аргумента В.
|
|
|
В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие: «если….то...», «... тогда и только тогда, когда...» и др. Некоторые из них имеют своё название и свой символ, и им соответствуют определённые логические функции.
|
|
|
