 |
Задания для самостоятельной работы
|
|
|
|
Рассчитать среднюю проницаемость неоднородного пласта, состоящего из i – цилиндрических дренируемых, изолированных между собой зон, если радиус скважины – rс, радиус контура питания – rк; радиусы дренируемых зон – ri; с проницаемостью ki, мД:
ri – радиусы дренируемых зон, м;
ki – проницаемость дренируемых зон, мД;
rс – радиус скважины, см;
rк – радиус контура питания, м;
1,..., 120 – номер варианта.
Исходные данные представлены в таблице 2.3.
Таблица 2.3
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
Продолжение табл. 2.3
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
Продолжение табл. 2.3
|
|
|
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
Продолжение табл. 2.3
|
|
|
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
Продолжение табл. 2.3
| В | ||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||
| В | ||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||
| В | ||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||
| В | ||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||
| В | ||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||
Продолжение табл. 2.3
|
|
|
| В | ||||||||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||||||||
| В | ||||||||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||||||||
| В | ||||||||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||||||||
| В | ||||||||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||||||||
| В | ||||||||||||||||||||||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||||||||||||||||||||||
| rc= | rc= | rc= | rc= | |||||||||||||||||||||||||||||
| rk= | rk= | rk= | rk= | |||||||||||||||||||||||||||||
Продолжение табл. 2.3
|
|
|
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
| В | ||||||||||||
| Ni | ri | ki | ri | ki | ri | ki | ri | ki | ||||
| rc= | rc= | rc= | rc= | |||||||||
| rk= | rk= | rk= | rk= | |||||||||
Расчет дебита фильтрующейся жидкости для различных видов пористости
Оценка дебита жидкости при линейном режиме равномерной фильтрации
Теория к разделу
Рассмотрим случай субкапиллярной фильтрации, т.е. фильтрация равномерная и проходит через всю площадь образца, имеющего субкапиллярную пористость.
Дебит жидкости при линейном режиме оценивается уравнением Дарси:
 , (3.1)
, (3.1)
где kпр – проницаемость, Д;
F – площадь фильтрации, см2;
∆P – перепад давления, атм;
m – вязкость, спз;
L – длина, см.
Типовая задача
Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мД, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. Определить дебит жидкости.
Дано:
kпр = 10 мД = 0,01 Д;
F = 100 см2;
∆P/L = 0,25 атм/м = 0,0025 атм/см;
m = 1 спз.
Найти: Q1
Решение:
 ,
,
 .
.
Оценка дебита жидкости при неравномерно-проницаемой фильтрации
Теория к разделу
Проницаемость жидкости при фильтрации через капилляр оцениваем из соотношения уравнений Дарси:
 (3.2)
(3.2)
и Пуазейля:
 , (3.3)
, (3.3)
откуда:
 , (3.4)
, (3.4)
где kпр.кап – проницаемость при фильтрации жидкости через капилляр, Д;
F – площадь фильтрации, см2;
∆P – перепад давления, атм;
m – вязкость, спз;
L – длина, см.
После преобразования коэффициента проницаемости и радиуса капилляра к одной размерности получим эмпирическое уравнение для оценки коэффициента проницаемости при фильтрации жидкости через капилляр:
|
|
|
 . (3.5)
. (3.5)
Типовая задача
Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мДарси, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. В этом кубике существует один капилляр диаметром 0,2 мм. На сколько увеличится суммарный дебит при прочих равных параметрах m и ∆P/L?
Дано:
Dк = 0,2 мм = 0,02 см;
∆P/L = 0,25 атм/м = 0,0025 атм/см;
m = 1 спз;
Nк =1.
Найти: Q2 - дебит при фильтрации через капилляр;
Q3 - суммарный дебит за счёт субкапиллярной и капиллярной фильтрации.
Решение:
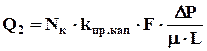 ,
,

 ,
,
 .
.
Рассчитаем дебит через этот капилляр:
 ,
,
 .
.
По сравнению с субкапиллярной проницаемостью (kпр = 10 мД) дебит увеличится при наличии одного такого канала на 40% (Q2 / Q1), а если бы субкапиллярная проницаемость была kпр = 1 мД, то дебит увеличился бы на 400% (Q2 / Q1 × kпр).
|
|
|


