Оценка дебита жидкости при наличии трещиноватой фильтрации

Теория к разделу

Допустим, в кубике с субкапиллярной проницаемостью вместо канала имеется трещина вдоль всего образца шириной L_тр, высотой h_тр.

Оценить проницаемость трещины (щели) для жидкости, фильтрующейся через образец, можно, используя соотношение уравнений Буссинеска и Дарси:

, (3.6)

, (3.7)

где k_пр.тр – проницаемость при наличии трещиноватой фильтрации, Д;

v – линейная скорость движения жидкости, см/с;

∆P – перепад давления, атм;

m – вязкость, спз;

L_тр – ширина трещины, см;

h_тр – высота трещины, см.

Приведя параметры к одной размерности в единицах измерения нефтепромысловой геологии, получим эмпирическое уравнение для оценки коэффициента проницаемости при трещиноватой фильтрации:

. (3.8)

Типовая задача

 

Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мДарси, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. В этом кубике будет существовать одна трещина шириной 10 см, высотой 0,2 мм. На сколько увеличится суммарный дебит при прочих равных параметрах m и ∆P/L?

 

Дано:

h_тр = 0,2 мм = 0,02 см;

∆P/L = 0,25 атм/м =0,0025 атм/см;

m = 1 спз;

L_тр = 10 см;

М_тр = 1.

 

Найти: Q₄ - дебит при фильтрации через трещину;

Q₅ - суммарный дебит жидкости за счет субкапиллярной и трещиноватой фильтрации.

Решение:

,

,

.

,

а суммарный дебит с учетом субкапиллярной фильтрации:

.

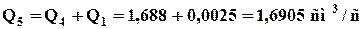Сравнивая дебиты Q₄ и Q₁, получим, что наличие общей трещины приводит к увеличению дебита в 675 раз (1,688 / 0,0025).

 

Задания для самостоятельной работы

 

Дан кубик породы размером 10х10х10 см. Определить дебиты (Q₁),(Q₂),(Q₃),(Q₄),(Q₅)при:

1. равномерной субкапиллярной и неравномерно-проницаемой фильтрациях;

2. равномерной субкапиллярной и трещиноватой фильтрациях

и сравнить их для условий, представленных в таблице 3.1, имеющих следующие обозначения:

k_пр – проницаемость при субкапиллярной фильтрации, мД;

m – вязкость жидкости, спз;

∆Р/L – перепад давления, атм/м;

N_к – число капилляров;

D_к – диаметр капилляра, мм;

L_тр – длина трещин, см;

h_тр – высота трещины, мм;

М_тр – число трещин;

1,..., 120 – номер варианта.

Таблица 3.1

B
kпр
m	2,0	1,3	3,0	2,5	3,0	1,5	2,0	1,3	3,0	1,2	1,4
ΔP/L	0,3	0,26	0,31	0,32	0,33	0,35	0,3	0,36	0,31	0,28	0,26
Nk
Dk	0,18	0,2	0,22	0,24	0,25	0,16	0,3	0,27	0,28	0,24	0,16
Lтр
hтр	0,15	0,16	0,18	0,17	0,19	0,22	0,21	0,28	0,27	0,28	0,23
Мтр
B
kпр
m	1,8	2,0	2,2	2,5	3,0	2,8	2,2	1,1	1,3	1,1	1,8
ΔP/L	0,3	0,24	0,22	0,23	0,26	0,25	0,3	0,36	0,26	0,27	0,24
Nk
Dk	0,15	0,22	0,23	0,24	0,33	0,28	0,26	0,3	0,18	0,19	0,21
Lтр
hтр	0,22	0,21	0,23	0,19	0,22	0,23	0,25	0,26	0,27	0,28	0,22
Мтр
B
kпр
m	1,6	1,9	2,0	3,0	1,4	1,8	1,6	2,2	2,0	2,1	1,3
ΔP/L	0,2	0,22	0,24	0,25	0,31	0,32	0,28	0,24	0,25	0,28	0,31
Nk
Dk	0,22	0,23	0,25	0,26	0,27	0,28	0,3	0,31	0,29	0,28	0,18
Lтр
hтр	0,24	0,26	0,28	0,16	0,25	0,26	0,27	0,18	0,23	0,24	0,22
Мтр

Продолжение табл. 3.1

 

B
kпр
m	1,6	1,7	3,0	1,6	1,8	1,9	2,8	3,0	2,0	2,0	1,3
ΔP/L	0,4	0,28	0,35	0,37	0,39	0,4	0,22	0,28	0,3	0,28	0,24
Nk
Dk	0,22	0,26	0,3	0,31	0,28	0,29	0,26	0,2	0,25	0,18	0,2
Lтр
hтр	0,2	0,26	0,26	0,28	0,29	0,3	0,18	0,26	0,24	0,27	0,18
Мтр
B
kпр
m	3,0	2,5	3,0	1,5		1,3	3,0	1,2	1,4	1,8	2,0
ΔP/L	0,25	0,28	0,31	0,4	0,28	0,35	0,37	0,39	0,4	0,22	0,28
Nk
Dk	0,22	0,24	0,25	0,16	0,3	0,27	0,28	0,24	0,16	0,15	0,22
Lтр
hтр	0,23	0,24	0,22	0,2	0,26	0,26	0,28	0,29	0,3	0,18	0,26
Мтр
B
kпр
m	2,2	2,5	3,0	2,8	2,2	1,1	1,3	1,1	1,8	1,6	1,9
ΔP/L	0,3	0,23	0,26	0,25	0,3	0,36	0,26	0,27	0,24	0,2	0,22
Nk
Dk	0,23	0,24	0,33	0,28	0,26	0,3	0,22	0,19	0,21	0,22	0,23
Lтр
hтр	0,24	0,15	0,16	0,18	0,17	0,19	0,18	0,21	0,28	0,27	0,28
Мтр

 

Продолжение табл. 3.1

 

B
kпр
m	2,0	3,0	1,4	1,8	1,6	2,2	2,0	2,1	1,3	1,6	1,7
ΔP/L	0,24	0,25	0,31	0,32	0,3	0,26	0,31	0,32	0,33	0,35	0,3
Nk
Dk	0,25	0,26	0,27	0,28	0,3	0,31	0,29	0,28	0,18	0,2	0,26
Lтр
hтр	0,23	0,22	0,21	0,23	0,19	0,22	0,23	0,25	0,26	0,27	0,28
Мтр
B
kпр
m		2,8	2,2	1,1	1,3	1,1	1,8	1,6	1,3		2,5
ΔP/L	0,28	0,31	0,4	0,28	0,35	0,37	0,39	0,4	0,3	0,32	0,33
Nk
Dk	0,26	0,3	0,18	0,19	0,21	0,22	0,23	0,25	0,25	0,16	0,3
Lтр
hтр	0,23	0,24	0,22	0,2	0,26	0,26	0,28	0,29	0,21	0,28	0,27
Мтр
B
kпр
m		1,5		1,3		1,2	1,4	1,8		2,2	2,8
ΔP/L	0,35	0,3	0,36	0,31	0,28	0,26	0,3	0,24	0,22	0,23	0,3
Nk
Dk	0,27	0,28	0,24	0,16	0,15	0,22	0,23	0,24	0,33	0,28	0,18
Lтр
hтр	0,28	0,23	0,22	0,21	0,23	0,19	0,22	0,25	0,25	0,26	0,22
Мтр

 

Продолжение табл. 3.1

 

B
kпр
m	2,2	1,1	1,3	1,1	1,8	1,6		2,1	1,3	1,6	1,7
ΔP/L	0,36	0,26	0,27	0,24	0,2	0,22	0,25	0,31	0,4	0,28	0,35
Nk
Dk	0,19	0,21	0,22	0,23	0,25	0,26	0,28	0,26	0,3	0,31	0,28
Lтр
hтр	0,24	0,26	0,28	0,16	0,28	0,25	0,18	0,28	0,29	0,3	0,18
Мтр
B
kпр
m		2,8		2,5	2,2		1,8		1,3
ΔP/L	0,26	0,26	0,23	0,3	0,28	0,22	0,4	0,35	0,28	0,25
Nk
Dk	0,24	0,23	0,22	0,15	0,16	0,24	0,28	0,21	0,25	0,29
Lтр
hтр	0,22	0,18	0,3	0,28	0,28	0,26	0,22	0,27	0,24	0,28
Мтр

 

 

Состояние нефтяных газов в пластовых условиях

 

Теория к разделу

В пластовых условиях газы в зависимости от их состава, давления и температуры (термобарического режима в пласте) могут находиться в различных агрегатных состояниях – газообразном, жидком, в виде газожидкостных смесей.

Природные газы, добываемые из газовых, газоконденсатных и нефтяных месторождений, состоят из углеводородов (УВ) метанового ряда СН₄-С₄Н₁₀: метана, этана, пропана, изобутана и н-бутана, а также неуглеводородных компонентов: H₂S, N₂, CO, CO₂, H₂, Ar, He, Kr, Xe и других.

Состав газовых смесей выражается в виде массовой или объемной концентрации компонентов в процентах и мольных долях:

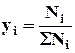, (4.1)

где N_i - масса i-го компонента;

Σ N_i - суммарная масса смеси.

, (4.2)

где V_i - объем i-го компонента в смеси;

Σ V_i - суммарный объем газа.

, (4.3)

где n_i - число молей i-го компонента в смеси;

Σ n_i - суммарное число молей газа в системе.

Уравнение состояния Клапейрона–Менделеева связывает давление, температуру и объем газа, представленного в виде физически однородной системы, при условиях термодинамического равновесия.

, (4.4)

где Р – давление, Па;

V – объем газа, м³;

G – масса газа, кг;

R – газовая постоянная, Дж/(кг • К);

T – абсолютная температура, К.

Газовая постоянная R численно равна работе расширения 1 кг идеального газа в изобарическом процессе при увеличении температуры газа на 1 К.

Уравнение состояния Клапейрона–Менделеева справедливо для идеального газа и для нефтяных систем работает в области давлений, близких к атмосферному. При давлениях Р > 10 атм нефтяной газ из идеальной системы переходит в неидеальную и описывается уравнением Клайперона-Менделеева с коэффициентом сжимаемости z, который учитывает отклонение реальных газов от законов сжатия и расширения идеальных газов.

Ниже записано уравнение состояния смеси газов в пластовых условиях, выраженное через мольные доли компонентов:

. (4.5)

Коэффициент сжимаемости газа z функционально зависит от приведенных давлений и температур, z = f (T_прив, Р_прив).

С приближением давления и температуры к их критическим значениям свойства газовой и жидких фаз становятся одинаковыми, поверхность раздела между ними исчезает и плотности их уравниваются.

Критическая температура (Т_кр) – максимальная температура, при которой свойства газовой и жидкой фаз находятся в равновесии.

Критическое давление (Р_кр) – давление паров вещества при критической температуре.

Среднекритические (псевдокритические) параметры смеси газов определяются по правилу аддитивности:

, (4.6)

. (4.7)

Приведенными параметрамисмеси газов называются безразмерные величины, показывающие, во сколько раз действительные параметры состояния газа: температура, давление, объем, плотность и другие больше или меньше среднекритических.

, (4.8)

. (4.9)

В соответствии с законом Авогадро один моль газа занимает объем при нормальных условиях 22,414 л, а при стандартных условиях 24,055л.

Нормальным условиям (н.у.) соответствуют абсолютная температура 273,15 К и абсолютное давление 0,1 МПа.

Стандартным условиям (с.у.) соответствуют температура 20°С (293,15 К) и абсолютное давление 0,1 МПа.

Объем газа в пластовых условиях определяется из соотношения Бойля-Мариотта:

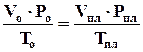, (4.10)

, (4.11)

. (4.12)

Объемный коэффициент газа оценивается отношением объема газа в пластовых условиях к объему, занимаемому газом при н.у.:

, (4.13)

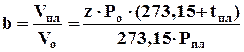. (4.14)

Типовая задача

Дана исходная таблица. Используя ее, мы определяем коэффициенты сжимаемости (z) и объемный коэффициент газа (b), занимающего первоначальный объем (V_о) 1000 м³ при нормальных условиях для пластовых условий: Р_пл = 100 атм, t_пл = 50°С, следующего состава (V_i,%) (табл. 4.1):

Таблица 4.1

 

Компонент, Vi	%
метан (СН4)
этан (С2H6)
пропан (C3H8)	5,1
изобутан (i-C4H10)	0,8
н-бутан (n-C4H10)	1,7
изопентан (i-C5H12)	0,6
н-пентан (n-C5H12)	0,3
гексаны (C6H12)	0,5

Решение:

1) Рассчитываем приведенное давление по формуле:

. (4.15)

Для расчета Р_пр и T_пр используем критическое давление и критическую температуру смеси газов. Данные для каждого компонента представлены в таблице 4.2.

Таблица 4.2

 

Компонент	Ni, доли	Pкр, атм	Ткр, К	Ni • Pi кр, атм	Ni • Ti кр, К
СН4	0,82	47,32		38,80	156,62
С2H6	0,09	49,78		4,48	27,45
C3H8	0,051	43,38		2,21	18,87
i-C4H10	0,008	38,25		0,31	3,26
n-C4H10	0,017	38,74		0,66	7,23
i-C5H12	0,006	33,89		0,20	2,77
n-C5H12	0,003	34,1		0,10	1,41
C6H12	0,005	30,52		0,15	2,54
				S = 46,92	S = 220,14

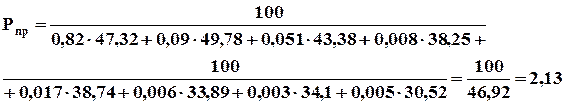
2) Рассчитываем приведенную температуру по формуле:

. (4.16)

Для расчета T_пр используем критические температуры компонентов Т_{i кр}. Данные для каждого компонента представлены в таблице 4.2.

3) Определяем z по графикам z = f (P) при Т = const (рис.4.1), (Оркин К. Г. стр. 90, Гиматудинов Ш.К. стр. 97, Амикс Дж. cтр. 237). Для нашего случая z = 0,81.

4) Объем газа в пластовых условиях определяем, используя закон Бойля–Мариотта (формула 4.12):

,

.

5) Объемный коэффициент газа оценивается отношением объемов газа в пластовых условиях к объему при н.у. (формула 4.14):

,

.

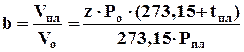Рис. 4.1.Графики зависимости коэффициента сверхсжимаемости Z углеводородного газа от приведенных псевдокритических давления Р_пр и температуры Т_пр (по Г.Г. Брауну). Шифр кривых – значения Т_пр

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: