Главная | Обратная связь | Поможем написать вашу работу!

Акции, облигации, дисконтирование, компаундинг

дюрация финансовый прибыль

1) Найдите дюрацию облигации сроком до погашения 10 лет, купонной ставкой 10% и номиналом 114 тыс. рублей, которая продаётся по цене 90 тыс. руб.

Решение

Дюрация - одно из фундаментальных понятий инвестиционного анализа. Понятие «дюрация» было впервые введено американским ученым Ф. Маколи (F.R. Macaulay) и играет важнейшую роль в анализе долгосрочных ценных бумаг с фиксированным доходом. Дюрация - средневзвешенная продолжительность потока платежей.

Смысл дюрации состоит в том, что инвестор пытается с ее помощью измерить риск своих вложений в облигации. По определению дюрация - это «временное ожидание» некоторого агрегированного денежного потока, который по финансовой значимости эквивалентен всей совокупности денежных выплат, связанных с облигацией.

Дюрация - это момент времени, когда происходит этот агрегированный платеж. Чем больше величина дюрации, тем более рискованным является вложение денег в данную облигацию. Дюрацию (D) можно рассчитать по формуле:

где:

С - купонный платёж;

r - процентная ставка за купонный период (требуемая доходность);

N - номинальная стоимость.

n - число купонных периодов.

P - текущая рыночная стоимость облигации.

Когда облигация продается по цене ниже номинала, говорят, что она продается с дисконтом.

Требуемая доходность такой облигации может быть рассчитана по формуле:

где К - купонная ставка.

r= 114 / 90 *10% = 12,7% или 0,127.

Расчёт дюрации Маколея приведен в таблице 1.1.

Таблица 1.1- Расчёт дюрации

Номер периода (n)

Денежный поток (Сn)

(1+r)ⁿ

Приведенная стоимость 1 денежной единицы (РV);

Приведенная стоимость денежного потока (РV*Cn)PV*Cn *n

11,4

1,127

0,8873

10,1152

11,4

1,27

0,7874

8,9764

17,9528

11,4

1,431

0,6988

7,9663

23,8989

11,4

1,613

0,6200

7,0680

28,272

11,4

1,818

0,5501

6,2711

31,3555

11,4

2,049

0,4880

5,5632

33,3792

11,4

2,309

0,4331

4,9373

34,5611

11,4

2,602

0,3843

4,3810

35,048

11,4

2,933

0,3409

3,8863

34,9767

125,4

3,305

0,3026

37,9460

379,46

Итого

97,1109

629,0194

Дюрация = 629,0194/ 97,1109= 6,477

Ответ: дюрация для данной облигации равна 6,477.

2) Фирме необходим кредит в сумме 14 млрд. рублей. Банк согласен на его выдачу при условии, что через 90 дней он получит 15,8 млрд. рублей. Определить уровень учетной ставки.

Решение

Обозначим через r учётную ставку. Так как фирма берёт кредит на 90 дней, то ставка, под которую он берёт кредит (r₁), составит:

Пусть С - сумма кредита, С₁ - сумма, которую фирма должна возвратить банку.

Тогда:

С₁ = С * (1+r₁) = C * (1 + 0,2466 *r)

Отсюда

r = (C₁/C - 1) / 0,2466 = [15,8 / 14 -1] / 0,2466 = 0,52 или 52 %

Ответ: учётная ставка составляет 52%.

) На счете в банке 19 млн. р. Банк платит 19% годовых (сложные проценты, начисление один раз в год). Предлагается войти всем капиталом в совместное предприятие, при этом прогнозируется удвоение капитала через 5 лет. Принимать ли это предложение?

Решение

Предложение следует принимать лишь в том случае, если доходы от участия в совместном предприятии превысят сумму, которая накопится в банке через 5 лет.

Сложные проценты - форма расчета дохода, основанная на присоединении к сумме долга начисленных, но невыплаченных процентов, начисление процентов на проценты, расчет процентов на два или большее число периодов, проводимый таким образом, что процент начисляется не только на исходную сумму, но и на процент, начисленный в предыдущем периоде. Сложные проценты - это такой вариант, при котором происходит капитализация процентов, т.е. их причисление к сумме вклада и последующий расчет дохода не от первоначальной, а от накопленной суммы вклада. Капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, такие периоды равны и чаще всего банки используют месяц, квартал или год.

В итоге, для расчета сложных процентов используется следующая формула:

= Sv * (1 + (R / Ny))^Nd,

где:- итоговая сумма;- начальная сумма;- годовая процентная ставка;- количество периодов капитализации в году;- количество периодов капитализации за весь период вклада.

В нашем случае капитализация в году отсутствует, поэтому формула примет вид:

= Sv * (1 + R) ^Nd,

Fv = 19 * (1+0,19)⁵ = 45,34(млн.р)

Таким образом, через 5 лет в банке будет получена сумма 45,34 млн.р., а если деньги будут вложены в совместное предприятие, то полученная сумма составит 38 млн.р (19 млн.р *2). Кроме того, при хранении денег в банке ниже риски.

Ответ: Предложение принимать не следует.

) Определите стоимость актива, который приносит ежегодный доход 34 млн. руб. при ставке дисконта 10%.

Решение

Доход от использования актива (D) рассчитывается по следующей формуле:

D = А * r / 100%

где

А - стоимость актива;

r - ставка дисконта, %

Отсюда А = D/r *100%;

А = 34 /10%*100% = 340 (млн.р)

Ответ: стоимость актива составляет 340 млн.р.

) Рассчитайте сегодняшнюю стоимость будущих доходов при условии, что аннуитет составит 114 тыс. руб. ежегодно в течение 17 лет, а ставка дисконтирования 10% годовых.

Решение

Аннуитетный платеж - вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.

Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом. Вторая часть идёт на погашение долга. Аннуитетная схема погашения отличается от дифференцированной тем, что в начале кредитного периода проценты составляют большую часть платежа. Тем самым сумма основного долга уменьшается медленно, соответственно переплата процентов при такой схеме погашения кредита получается больше.

При аннуитетной схеме выплат по кредиту, ежемесячный платёж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита.

Формула для расчета дисконтированного денежного потока:

- будущая стоимость;- текущая стоимость;- ставка дисконтирования;- количество лет.

Расчёт сегодняшней стоимости будущих денежных потоков представлен в таблице 1.2.

Таблица 1.2 - Расчёт сегодняшней стоимости будущих денежных потоков

Годы	Аннутет (FV)	(1+r)ⁿ	Приведенная стоимость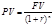
1-й	114	1,10000	103,6364
2-ой	114	1,21000	94,21488
3-й	114	1,33100	85,64989
4-ый	114	1,46410	77,86353
5-ый	114	1,61051	70,78503
6-ой	114	1,77156	64,35006
7-ой	114	1,94872	58,49994
8-ой	114	2,14359	53,18181
9-ый	114	2,35795	48,34708
10-ый	114	2,59374	43,95198
11-ый	114	2,85312	39,95626
12-ый	114	3,13843	36,32389
13-ый	114	3,45227	33,02175
14-ый	114	3,79750	30,01975
15-ый	114	4,17725	27,29068
16-ый	114	4,59497	24,80974
17-ый	114	5,05447	22,55429
Итого			914,4569

Ответ: Сегодняшняя стоимость будущих денежных потоков равна 914,457 тыс.руб.

12 3 4 Следующая ⇒

Воспользуйтесь поиском по сайту: