 |
Двухфакторный дисперсионный анализ
|
|
|
|
Двухфакторные комплексы по своей структуре более сложны, чем однофакторные.
Объединение в один статистический комплекс допускается только таких факторов, которые независимы друг от друга (например, тип кормления и доза облучения, возраст и пол и т.д.).
Чтобы построить двухфакторную дисперсионную модель все имеющиеся данные представим в виде табл. 1, в которой по строкам - уровни 
фактора А, по столбцам - уровни 
фактора В, а в соответствующих клетках, или ячейках, таблицы находятся значения признака 
(i=1,2…, m; j=1,2…, l; k=1,2…, n):
Таблица 1.
| В А | В1 | В2 | … | Вj | … | Вl |
| А1 | 
| 
| … | 
| … | 
|
| А2 | 
| 
| … | 
| … | 
|
| . . . | … | … | … | … | … | … |
| Аj | 
| 
| … | 
| … | 
|
| . . . | … | … | … | … | … | … |
| Аm | 
| 
| … | 
| … | 
|
Двухфакторная дисперсионная модель имеет вид:
(1)
где - значение наблюдения в ячейке ij c номером k;
- общая средняя;
- эффект, обусловленный влиянием i-го уровня фактора А;
- эффект, обусловленный влиянием j-го уровня фактора B;
- эффект, обусловленный взаимодействием двух факторов, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (1);
- возмущение, обусловленное вариацией переменной внутри отдельной ячейки.
Полагаем, что имеет нормальный закон распределения 
, а все математические ожидания 
равны нулю.
Групповые средние находятся по формулам:
в ячейке -
(2) 
по строке -
, (3)
по столбцу –
(4)
Общая средняя
(5)
Таблица дисперсионного анализа имеет вид:
Таблица 2
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты |
| Межгрупповая (фактор А) | 
| m-1 | 
|
| Межгрупповая (фактор В) | 
| l-1 | 
|
| Взаимодействие (АВ) | 
| (m-1)(l-1) | 
|
| Остаточная | 
| mln-ml | 
|
| Общая | 
| mln-1 |
|
|
|
Можно показать, что проверка нулевых гипотез 
об отсутствии влияния на рассматриваемую переменную факторов А, В и их взаимодействия АВ осуществляется сравнением отношений 
.
Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены, так как выпадает компонента 
из общей суммы квадратов отклонений, а с ней и средний квадрат 
, ибо в этом случае не может быть речи о взаимодействии факторов.
Пример. В табл. 3 приведены суточные привесы (г) отобранных для исследования 18 поросят в зависимости от метода содержания поросят (фактора А) и качества их кормления (фактор В).
Таблица 3.
| Количество голов в группе (фактор А) | Содержание протеина в корме, г (фактор В) | |
| В1=80 | В2=100 | |
| А1=30 | 530,540,550 | 600,620,580 |
| А2=100 | 490,510,520 | 550,540,560 |
| А3=300 | 430,420,450 | 470,460,430 |
Необходимо на уровне значимости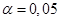 
оценить существенность (достоверность) влияния каждого фактора и их взаимодействия на суточный привес поросят.
Решение. Имеем m =3, l =2, n =3. Определим (в г) средние значения привеса:
в ячейках – по (формуле 2)
и аналогично 
;
по строкам – по (3):
и аналогично 
по столбцам – (4):
и аналогично 
Общий средний привес – по (5):
.
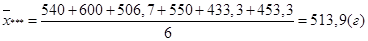Все средние значения привеса (г) поместим в табл. 3
Таблица 3.
| Количество голов в группе (фактор А) | Содержание протеина в корме, г (фактор В) | ||
| В1=80 | В2=100 | 
| |
| А1=30 | 
| 
| 
|
| А2=100 | 
| 
| 
|
| А3=300 | 
| 
| 
|
| 
| 
| 
|
Из табл. 3 следует, что с увеличением количества голов в группе средний суточный привес поросят в среднем уменьшается, а при увеличении содержания протеина в корме - в среднем увеличивается. Но является ли эта тенденция достоверной или объясняется случайными причинами? Для ответа на этот вопрос по формулам табл. 2 вычислим необходимые суммы квадратов отклонений:
;
;
Средние квадраты находим делением полученных сумм на соответствующие им число степеней свободы m-1=2, l-1=1; (m-1)(l-1)=2; mln-ml=18-6=12; mln-1=18-1=17.
|
|
|
Результаты расчета сведем в табл. 4.
Очевидно, данные факторы имеют фиксированные уровни, т.е. мы находимся в рамках модели I. Поэтому для проверки существенности влияния факторов А, В и их взаимодействия АВ необходимо найти отношения:
, 
и сравнить их с табличными значениями (см. приложение 6) соответственно 
Так как 
и 
, то влияние метода содержания поросят (фактор А) и качества их кормления (фактор В) является существенным. В силу того что 
взаимодействие указанных факторов незначимо (на 5%-ном уровне).
Таблица 4.
| Компонента дисперсии | Суммы квадратов | Число степеней свободы | Средние квадраты |
| Межгрупповая (фактор А) | 
| 
| |
| Межгрупповая (фактор В) | 
| 
| |
| Взаимодействие (АВ) | 
| 
| |
| Остаточная | 
| 
| |
| Общая | 
|
MS Excel в статистике
Широкое внедрение методов анализа данных в повседневную практику стимулировано распространением персональных компьютеров. Однако для осмысленной работы пользователь должен обладать определенной подготовкой: понимать, в каких ситуациях применимы различные статистические методы, знать их возможности и ограничения, уметь корректно интерпретировать результаты.
В настоящее время наиболее широко используемым программным обеспечением является программное обеспечение, работающее в среде Windows. Одним из составляющих программного обеспечения среды Windows, является программа Microsoft Excel, которая является мощным средством для работы с таблицами статистических данных. Она позволяет упорядочивать, обрабатывать определенным образом, графически представлять и анализировать различные виды статистической информации.
С помощью пакета анализа можно проводить следующие действия:
- генерировать случайные числа, подчиняющиеся различным законам распределения;
- проводить формирование выборки из генеральной совокупности;
- по выборке строить интервальный вариационный ряд, гистограмму, кумулятивную кривую и диаграмму Парето;
- вычислять точечные и интервальные оценки статистической совокупности;
- проводить сглаживание временных рядов;
- оценивать зависимость системы двух случайных величин;
- проверять статистические гипотезы с использованием различных критериев;
|
|
|
- проводить однофакторный и двухфакторный дисперсионный анализ;
- строить множественное уравнение регрессии;
- ранжировать статистические данные.
|
|
|
