 |
Выборочные центральные моменты. Асимметртя и эксцесс
|
|
|
|
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. Вводят специальные характеристики: асимметрию и эксцесс.
Асимметрия или коэффициент асимметрии (термин был введен впервые Пирсоном, 1895), является мерой несимметричности распределения. Если этот коэффициент значительно отличается от 0, распределение является асимметричным (т.е. несимметричным, сдвинуто влево или вправо). Для нормального распределения эти характеристики равны нулю.
Асимметрией теоретического распределения называют отношение центральногомомента третьего порядка к кубу среднего квадрата отклонения.
Центральным моментом порядка k случайной величины X называется математическим ожиданием величины (X – M(X)) k, обозначается через μk.
Таким образом, по определению
μk = M(X – M(X)) k.
В частности, μ 2 = D(X), то есть центральный момент 2-го порядка есть дисперсия
μ 1 = M(X – M(X)) = 0
Для дискретной случайной величины
 |
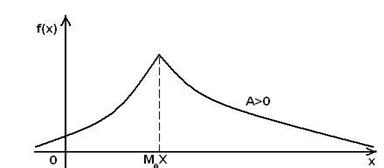
Если А > 0, то кривая распределения более полога справа от М0(X) (рис.13);
если А < 0, то кривая распределения более полога слева от М0(X) (рис.14).
 |
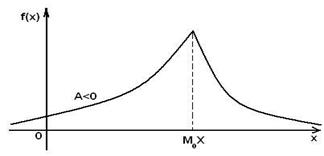Рис.13
Рис.14
Коэффициентом эксцесса Е ("островершинности" ) случайной величины X называется величина
 |
Эксцесс или коэффициент эксцесса (термин был впервые введен Пирсоном, 1905), измеряет остроту пика распределения. Величина Е характеризует островершинность или плосковершинность распределения. Если
Е > 0 – более островершинные, а распределения "плосковершинные" и “многовершинные” имеют Е < 0 (рис. 15)
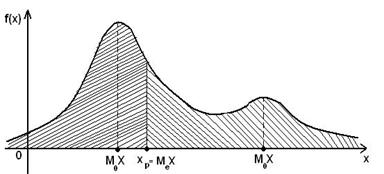
Рис.15
2.4.3. Показатели вариации: 
, 
(
), 
(S), 
, 
|
|
|
1. 
- размах
2. Для определения меры рассеяния значений количественного признака Х генеральной совокупности около генеральной средней вводят понятие генеральной дисперсии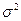 
В статистическом понимании генеральная дисперсия есть среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего арифметического.
Выборочной дисперсией называют среднее арифметическое квадратов отклонений значения наблюдаемых значений признака от выборочной средней.
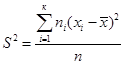(для n>30) - выборочная дисперсия, служит оценкой генеральной дисперсии.
(для 
) - исправленная выборочная дисперсия (несмещенная)
Дисперсия является важной характеристикой при генетическом анализе популяций и селекции животных. Здесь дисперсия служит характеристикой изменчивости некоторого признака особей данной совокупности.
3.Основным показателем изменчивости является среднее квадратическое отклонение S(выборочное), равное корню квадратному из дисперсии:
или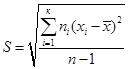 
(
) - исправленное
Среднее квадратическое отклонение не только характеризует изменчивость признака, но и выявляет особенности изменения признака у особей данной совокупности. Например, может быть такая ситуация, когда две сопоставляемые совокупности имеют одинаковые величины хmax, xmin и выборочную среднюю, но по особенностям изменения признака и величине среднего квадратического отклонения отличаются.
Пример. Нужно сопоставить изменчивость плодовитости самок песцов двух групп. В каждой группе было по пять самок. Показатели их плодовитости следующие:
| группа | Число щенков в помете | Номер самки в группе |
| 1 2 3 4 5 | ||
| 7 8 9 8 10 7 8 10 7 10 |
Среднее значение по группам:
головы; 
головы.
Среднее квадратическое отклонение по группам:
головы;
головы.
Следовательно, при одинаковых максимальных и минимальных значениях признака и средних арифметических сравниваемые ряды различаются по величине 
. Изменчивость плодовитости самок 2 группы оказалось выше, чем 1 группы.
|
|
|
4. Коэффициент вариации.
В практике довольно часто приходиться сравнивать изменчивость признаков, выраженных разными единицами. В таких случаях используют не абсолютные, а относительные показатели вариации.
Дисперсия и среднее квадратическое отклонение как величины, выражаемые теми же единицами, что и характеризуемый ими признак, для оценки изменчивости разноименных величин непригодны.
Относительной характеристикой колеблемости является коэффициент вариации Сv.
Коэффициентом вариации называется отношение среднего квадратического отклонения к величине средней, выраженное в процентах.
При симметричных распределениях Сv обычно не превышает 50%. При сильно ассиметричных рядах распределения Сv может достигать даже более 100%. Слабая вариация: 
; средняя 
; сильная 
.
Пример. Сравнивают два варьирующих признака:
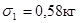
и 
и 
Следует ли отсюда, что 2-ой признак варьирует сильнее, чем 1-ый? Нет, т.к.
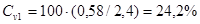
Сильнее варьирует 1-ый признак.
5. Нормированное отклонение t.
Использование среднего квадратичного отклонения позволяет выразить в относительном выражении степень отклонения какого – либо члена совокупности от средней арифметической данного ряда.
Для этого берут разность между значением данного варианта x и значением среднего арифметического 
и относят эту разность к среднему квадратичному отклонению . Полученное в результате такого отношения выражение 
называется нормированным отклонением t данного члена совокупности от среднего арифметического в долях .
Чем больше величина нормированного отклонения, тем дальше от отстоит данный вариант. Минимальное и максимальное значение вариантов имеют нормированное отклонение, равное 
и 
.
Степень свободы.
При рассмотрении понятия дисперсии и среднего квадратического отклонения мы столкнулись с величиной n-1, которая получила особое название – число степеней свободы. В дальнейшем мы будем обозначать эту величину буквой 
. Объясним подробнее его значение.
Рассмотрим некоторый вариационный ряд, в котором имеется n вариант. При известном значении средней выборочной этого ряда каждая отдельная варианта жестко связана с остальными n – 1 вариантами. То есть в данном случае имеется n – 1 степеней свободы. Так, например, если известно, что два кролика в сумме весят 7 кг, а один из них весит 3,5 кг, то вес второго уже точно определен весом первого, то есть имеется 
степеней свободы. Если известно, что 10 кроликов весят вместе 55 кг (т.е. выборочная средняя равна 5,5), то вес одного определяется весом девяти других, то есть имеется 
степеней свободы.
|
|
|
|
|
|
