 |
Оценка генеральной средней.
|
|
|
|
Теорема: Выборочная средняя 
повторной выборки есть несмещённая и состоятельная оценка генеральной средней 
, причем 
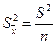- дисперсия выборочной средней.
Выборочная средняя повторной выборки для нормально распределенной генеральной совокупности является эффективной оценкой генеральной средней
Определение: Среднее квадратическое отклонение выборочной средней 
называется стандартной ошибкой выборки
- стандартная ошибка выборки
Величину средней и её стандартную ошибку записывают так: 
Ошибка средней арифметической может быть выражена в относительных величинах, т.е. в %. В этом случае её называют показателем точности 
и вычисляют по формуле:
 |
Относительная ошибка выборки показывает, на сколько процентов выборочная оценка отклоняется от параметра генеральной совокупности.
Чем меньше величина 
, тем достовернее, надёжнее полученная средняя. Точность средней арифметической является приемлемой, если этот коэффициент не превышает 5%.
При выборке малого объема точечная оценка может разительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам.
По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ.
Если δ > 0 и │Θ – Θ*│< δ, то чем меньше δ, тем оценка точнее.
Т.о., положительное число δ характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Θ* удовлетворяет неравенству │Θ – Θ*│< δ; можно лишь говорить о вероятности 
, с которой это неравенство осуществляется.
|
|
|
Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность , с которой осуществляется неравенство │Θ – Θ*│< δ
= 0,95; 0,99; 0,999.
Заменив неравенство │Θ – Θ*│< δ равносильным ему двойным неравенством
Вероятность того, что интервал (Θ* - δ; Θ* + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна .
Доверительным интервалом называется случайный интервал
(Θ*- δ; Θ*+ δ), в пределах которого с вероятностью находится неизвестный оцениваемый параметр.
Число называется доверительной вероятностью, уровнем доверия или надежностью оценки. Это значение задают заранее. Тогда, зная закон распределения случайной величины, можно найти доверительный интервал.
Число p(или 
) называется уровнем значимости и показывает, с какой вероятностью заключение о надежности оценки ошибочно.
Его находят по формуле
.
Величина может иметь три значения: 0,95; 0,99; 0,999.
Соответственно p: 0,05; 0,01; 0,001.
Очевидно, что чем меньше p, тем точнее оценка.
На рис.16 показан геометрический смысл доверительной вероятности, уровня значимости и доверительного интервала. Длина доверительного интервала определяется 
% (значение доверительной вероятности, выраженной в процентах) площади под нормальной кривой выборочного распределения некоторой случайной величины. Уровень значимости соответствует той оставшейся части (в %) площади под нормально кривой, которая выходит за границы доверительного интервала.
Рис.16 Доверительный интервал, уровень значимости 
, доверительная вероятность 
для кривой нормального распределения.
Например, доверительная вероятность 
означает, что длина искомого доверительного интервала ограничивается 95% площади под кривой нормального распределения, т.е. полученная интервальная оценка справедлива для 95% членов генеральной совокупности. Оставшиеся 5% могут иметь отклонения от значений полученной оценки. С увеличением доверительной вероятности (уменьшением уровня значимости) увеличивается длина доверительного интервала.
|
|
|
Определение: наибольшее отклонение 
оценки 
от оцениваемого параметра 
в частности, выборочной средней (или доли) от генеральной средней (или доли), которое возможно с заданной доверительной вероятностью , называется предельной ошибкой выборки
Ошибка является ошибкой репрезентативности (представительности) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть её (выборка), отобранная случайно.
Прежде, чем перейти к интервальным оценкам параметров распределения, рассмотрим некоторые важные распределения случайной величины.
|
|
|
