В социологическом исследовании

Социологические исследования обычно бывают выборочными, поскольку сплошной охват изучаемой совокупности требует недопустимо высоких материальных и временных затрат. Поэтому при проектировании исследования одна из главных задач состоит в формировании такой выборки, которая была бы одновременно и представительной, и экономичной.

Представительностью, или репрезентативностью выборки называют ее способность правильно отражать состояние дел в той совокупности социальных объектов, из которой она извлечена и для изучения которой предназначена - генеральной совокупности. Репрезентативность обеспечивается двумя классами достаточно строго формализованных процедур: во-первых, дизайном выборки (стратегией и процедурами ее формирования) и, во-вторых, расчетом ее минимального объема, который при выбранном дизайне способен обеспечить приемлемую точность результатов.

Понятие эффективности (экономичности) выборки связано со стоимостью выборочного исследования, которая непосредственно зависит как от объема выборки (сколько объектов исследовать), так и от ее дизайна (каких именно и где).

Дизайн (способ проектирования) выборки определяется характеристиками генеральной совокупности и целями исследования.

Генеральной совокупностью называется полное множество объектов, имеющих отношение к изучаемой проблеме. Строгое определение генеральной совокупности фактически формализует объект социологического исследования. Любое выборочное исследование имеет своей целью получить достоверные выводы, относящиеся именно к генеральной совокупности.

Генеральные совокупности делят на конечные и (практически) бесконечные, конкретные и гипотетические, однородные и неоднородные. К бесконечным относят совокупности объемом в несколько сотен тысяч объектов и более. Однородность рассматривается по отношению к исследуемой проблеме: одна и та же генеральная совокупность в некоторых исследованиях может рассматриваться как однородная, в других - как неоднородная. Конкретные и гипотетические совокупности различаются по возможности определить их реальный состав. Например, верующие в Республике Беларусь образуют бесконечную гипотетическую генеральную совокупность - невозможно до начала исследования определить, кто из жителей нашей страны является верующим, а кто нет. Генеральная совокупность узбеков, проживающих в Беларуси, также является гипотетической по доступности, но вполне конечной по своей численности.

По своим целям научные исследования делятся на описательные и аналитические. Первоначально описательные исследования предназначались исключительно для получения обобщенных сведений о генеральной совокупности. Выборки таких исследований должны в определенном смысле "воспроизводить" ее изучаемые свойства.

Аналитические исследования проводятся с целью проверки гипотез о природе сил, действующих в генеральной совокупности. Традиционно такие исследования проектируются в рамках теории научного эксперимента, делающей свои выводы на основе сравнительного анализа отдельных групп объектов с определенными свойствами. При этом предполагается, что группы имеют одинаковый объем и формируются в одинаковых условиях, т.е. не

отличаются по характеристикам, которые не изучаются в данном исследовании. Такой выборочный дизайн называется экспериментальным.

Развитие статистики в последние десятилетия значительно либерализировало взгляды на организацию исследований: аналитические задачи стали решаться на основе не только экспериментальных, но и описательных выборок. Однако необходимо помнить, что сочетание описательных и аналитических целей в одном исследовании возможно далеко не всегда. В дальнейшем мы будем иметь в виду преимущественно описательные выборки.

Если рассматривать выборку как средство изучения генеральной совокупности, то становится очевидным основное требование к ней - возможность обобщения результатов выборочного исследования на генеральную совокупность. Именно соответствие выборки этому требованию, а не формальное воспроизведение в ней, например, социально-демографической структуры населения, определяет ее репрезентативность.

Обобщение результатов выборочного исследования на генеральную совокупность осуществляется с помощью строгих индуктивных процедур статистического вывода, который включает два основных направления, соответствующих двум целям выборочных исследований: статистическое оценивание, применяемое в описательных исследованиях, и статистическая проверка гипотез - в исследованиях, осуществляемых с аналитическими целями. Возможность таких обобщений основывается на теоретических выводах математической статистики, а они, в свою очередь, - на случайном отборе объектов из генеральной совокупности и приложениях теории вероятности.

Простой случайный отбор из генеральной совокупности предполагает, что: 1) генеральная совокупность однородна; 2) все ее элементы доступны для исследования в одинаковой степени; 3) имеется полный список элементов, составляющих генеральную совокупность; 4) к этому списку применяются процедуры случайного отбора (с использованием таблиц или генераторов случайных чисел).

При правильной организации простого случайного отбора все элементы генеральной совокупности получают одинаковую вероятность попадания в выборку, что зна-

чительно упрощает ее статистическое обоснование. Однако на практике извлечение простых случайных выборок из больших генеральных совокупностей часто оказывается слишком сложным и дорогостоящим, а иногда и, в принципе, невозможным.

Основными проблемами простого случайного отбора являются: 1) сложность и неоднозначность понятия однородности генеральной совокупности; 2) невозможность получения ее полных списков; 3) разная степень доступности респондентов и их готовности участвовать в исследовании.

Проектированием выборок при нарушении условий простого случайного отбора занимается специальная научная дисциплина - теория выборки в социальных исследованиях. В рамках этой теории разработаны разнообразные стратегии и способы извлечения выборок, применяемые в тех случаях, когда простой случайный отбор невозможен или требует недопустимо высоких затрат.

Прежде всего, теория выборки признает, что генеральные совокупности в социальных исследованиях часто неоднородны, имеют сложную структуру и (или) гипотетический характер, могут со временем менять свой состав. Поэтому прежде, чем начинать отбор, необходимо обеспечить основу выборки - достаточно полный перечень элементов генеральной совокупности, называемых единицами наблюдения. В качестве единиц наблюдения обычно выступают отдельные индивидуумы (респонденты) или семьи, но могут рассматриваться и более крупные сообщества - академические группы и целые учебные заведения, организации, предприятия, отдельные населенные пункты, регионы, страны. В идеальном случае основа выборки совпадает с генеральной совокупностью, на практике часто бывает несколько уже. Способность реальной основы выборки представлять генеральную совокупность обосновывается теоретически, на основании дополнительной информации.

К большим генеральным совокупностям со сложной структурой часто применяют многоступенчатый отбор. Для этого генеральную совокупность структурируют, разбивая ее на конечное число подсовокупностей. Образуется новая, конкретная и конечная, генеральная совокупность,

элементами (единицами отбора) которой являются выделенные подсовокупности. Часть из них отбирается для продолжения исследования. Эта операция может повторяться несколько раз, пока не будут получены подсовокупности, доступные для непосредственного изучения, причем на разных ступенях могут использоваться разные методы отбора и репрезентации.

При многоступенчатом отборе основой выборки на каждой ступени является список выделенных структурных единиц отбора. На последней ступени единицы отбора совпадают с единицами наблюдения - объектами из генеральной совокупности, включенными в выборку и подлежащими непосредственному исследованию.

Методы извлечения выборок делятся на вероятностные (статистические) и целевые (нестатистические). К вероятностным методам, кроме простого, относят стратифицированный и гнездовой (кластерный) случайный отбор, а также так называемые квазислучайные методы -систематический отбор и различные рандомизирующие процедуры ("маршрутная" территориальная выборка, отбор "случайного" респондента в семье и т.п.). К целевым относятся квотные и "доступные" выборки, методы основного массива, типичных представителей, "снежного кома", отбор экспертов, а также выборки с экспериментальным дизайном.

Систематический отбор представляет собой отбор из списка с определенным "шагом" (через определенное количество номеров). Эта процедура часто является более удобной, чем простой случайный отбор. Считается, что если в списках нет никаких циклических закономерностей, процедура дает результаты, аналогичные случайному отбору, а для списков, упорядоченных по размеру (например, населенных пунктов), - даже более точные.

Стратифицированные выборки применяют для неоднородных генеральных совокупностей и в тех случаях, когда списки объектов легче получить по частям, чем по генеральной совокупности в целом. В случае стратифицированного случайного отбора объем выборки делится между стратами пропорционально их численности, и затем из каждой страты извлекается простая случайная выборка. Например, к такому объекту исследования, как

население Беларуси, обычно применяют территориальную стратификацию по областям (можно воспользоваться данными областных адресных столов); при изучении минского студенчества есть смысл стратифицировать генеральную совокупность по вузам, а внутри вузов - по факультетам. Стратификацию по территориальному признаку иногда называют районированием.

Гнездовой (кластерный) отбор применяют к генеральным совокупностям, которые естественным образом делятся на достаточно мелкие составные части (гнезда или кластеры), различия между которыми по сравнению с различиями между объектами внутри кластеров невелики. В качестве кластеров часто используются академические классы и группы, однотипные дома в городском квартале, населенные пункты одной местности с приблизительно одинаковым числом жителей. Их отбирают случайным образом (иногда с вероятностью, пропорциональной их численности), а затем исследуют полностью (академические группы) или выборочно (населенные пункты).

Основным нестатистическим методом извлечения выборок является квотный отбор. Его применяют, если распределение генеральной совокупности по основным социально-демографическим или другим существенным для исследования признакам известно, но ее списки получить невозможно или для осуществления случайного отбора недостаточно времени и средств. В этом случае интервьюерам поручают опросить определенное число лиц с заданными характеристиками, отбирая их по своему усмотрению. Квотный отбор критикуется специалистами по теории выборки главным образом за то, что точность результатов, полученных по квотным выборкам, не может быть оценена статистически. Однако на практике он достаточно популярен благодаря своей простоте, относительно низкой стоимости и анонимности. Считается, что при исследовании общественного мнения, ценностей, установок, мотивов квотный отбор дает удовлетворительные результаты. Однако его категорически не рекомендуется использовать в исследованиях социальной структуры, стратификации, мобильности.

Экспериментальные выборки представляют собой частный случай квотных, однако их целью является репре-

зентация не всей генеральной совокупности, а тех ее частей, сравнение которых является целью исследования. Другим частным случаем квотных выборок является отбор типичных представителей каких-либо групп или экспертов по изучаемым проблемам.

Метод основного массива применяется на небольших генеральных совокупностях, для которых нет смысла проводить выборочное исследование. Обоснование репрезентативности в этом случае носит внестатистический характер, оно осуществляется посредством сравнения исследованной и неисследованной частей совокупности.

Наиболее уязвимым с точки зрения соответствия полученных результатов реальному положению дел является метод доступной выборки, который применяется при исследовании генеральных совокупностей, слишком сложных для исследования другими методами. Обычно это гипотетические генеральные совокупности - аудитория СМИ (опрашиваемая непосредственно через СМИ), потребители определенных товаров (опрашиваемые в магазинах), национальные меньшинства, представителей которых опрашивают в культурных обществах или в местах компактного проживания и т.п.

Метод "снежного кома" представляет собой нечто среднее между методами доступной выборки и основного массива. Он применяется к малочисленным гипотетическим генеральным совокупностям - например, к коллекционерам или экспертам по узкой проблеме. Каждого найденного члена такой совокупности спрашивают, кого из своих коллег он знает. Таким образом составляется основа выборки; процесс продолжается до тех пор, пока имена в списке не начнут повторяться.

Результаты выборочных исследований всегда отчасти не определены. Это происходит потому, что изучается только часть генеральной совокупности, и измерения производятся с ошибками. Однако при отсутствии грубых просчетов в планировании и реализации выборки эти ошибки можно контролировать, т.е. с высокой вероятностью полагать, что они находятся в некоторых пределах, которые представляются исследователю допустимыми В этой связи необходимо иметь представление об ошибках выборки.

Ошибкой выборки для некоторого показателя называется разность между его средними арифметическими значениями по выборке и по генеральной совокупности. Обычно выделяют две составляющие ошибки выборки, одну из которых называют систематической,. а другую случайной ошибкой.

Систематическая ошибка представляет собой некоторое смещение выборочного среднего значения признака по отношению к среднему генеральной совокупности, не уменьшающееся с увеличением объема выборки. Систематические ошибки обычно связывают с ошибками проектирования (дизайна) выборки (определением генеральной совокупности, выбором процедур извлечения выборки и сбора информации), а также с такими объективными обстоятельствами, как разная степень доступности респондентов и их готовности участвовать в исследовании. Систематические ошибки обычно трудно обнаружить и еще труднее измерить. Для этого проводятся специальные методологические исследования и применяются специальные процедуры тестирования выборки. Иногда они могут быть определены, если со временем становится известно распределение признака в генеральной совокупности (например, результаты выборов) или в результате скрупулезного анализа артефактов, обнаруженных при анализе данных исследования.

Случайные ошибки связаны с вероятностным характером процедур извлечения выборки из генеральной совокупности и ошибками измерения, не имеющими систематического характера. Ошибки такого рода неустранимы, но они подчиняются статистическим законам и, соответственно, поддаются контролю. Одно из важнейших свойств случайных ошибок состоит в том, что они уменьшаются с увеличением объема выборки. Следовательно, увеличивая объем выборки, их можно свести к допустимому пределу и тем самым обеспечить желательную степень точности результатов исследования.

Степень точности для каждого показателя в описательных исследованиях задается (и измеряется) двумя количественными характеристиками: величиной предельно допустимой случайной ошибки и вероятностью того, что эта ошибка не будет превышена (доверительной вероят-

ностью). Обе эти величины существенным образом зависят от объема выборки и способа ее извлечения. Стремление повысить точность приводит к быстрому росту необходимого объема выборки и, соответственно, стоимости исследования. Таким образом, каждая реализованная выборка является компромиссом между желательной степенью точности и имеющимися в распоряжении исследователя временными и материальными ресурсами.

Другой серьезной проблемой является разная степень точности одной и той же выборки для разных изучаемых показателей. В этой сложной ситуации мы рекомендуем ориентироваться в первую очередь на достижение удовлетворительной точности для признаков, наиболее важных с точки зрения целей исследования.

Поскольку в реальном исследовании среднее значение признака по генеральной совокупности обычно неизвестно (напротив, исследование проводится с целью его оценить), ошибка выборки не может быть вычислена точно, а только оценена статистическими методами. Сразу оговоримся, что статистическое оценивание ошибок возможно только для вероятностных выборок, на всех ступенях которых применяются случайные, систематические и рандомизирующие методы отбора, и при этом оценивается только случайная составляющая ошибки, а ее систематическая составляющая полагается равной нулю.

Случайные ошибки простой случайной выборки из бесконечной генеральной совокупности имеют распределение, близкое к нормальному, с нулевым средним и дисперсией, равной s²/n, где s² - дисперсия признака по

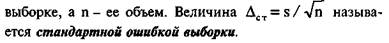
Из свойств случайной ошибки следуют два важных обстоятельства. Во-первых, значения таких ошибок обычно невелики. С вероятностью (1 - а) они не выходят за

пределы так называемого доверительного интервала, который имеет вид:

Формулы (1) и (2) применяются для оценки ошибки выборки после завершения исследования. Однако во многих случаях необходимо оценить до его начала, какой объем выборки при выбранном дизайне может обеспечить необходимую точность результатов.

Точность исследования для каждого признака задается двумя численными величинами: максимально допус-

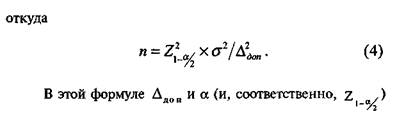
задаются исследователем произвольно, а дисперсия генеральной совокупности, если она неизвестна, должна быть предварительно оценена.

Если генеральная совокупность конечна, дисперсию выборочной ошибки следует вычислять с поправкой на ее

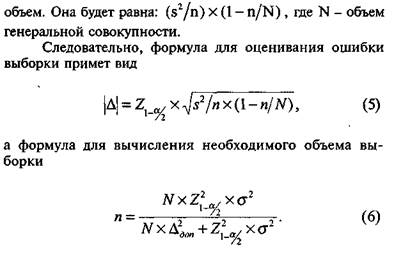
Приведенные выше формулы справедливы для простой случайной выборки. При более сложном дизайне применяются более сложные оценки выборочной ошибки и необходимого объема выборки.

Экономической эффективности выборок в отечественной литературе особого внимания не уделялось. Однако сейчас в условиях быстрого роста стоимости социологических исследований эта проблема становится все более актуальной. Понятие эффективности выборки связано с понятиями издержек на исследование и его точностью. Эффективными называются выборки, дизайн которых обеспечивает минимальные издержки при заданной

степени точности или максимальную точность результатов при заданных издержках. Проблема соотнесения издержек с точностью результатов сложна не только математически, но и организационно, так как требует скрупулезного учета стоимости всех предстоящих операций и накладных расходов.

Методы сбора

⇐ Предыдущая18192021222324252627Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: