 |
Прогнозирование методом подбора функций.
|
|
|
|
1. По уравнениюпрямой линии
Выравнивание и прогнозирование производится:

где уi' – выровненный и прогнозный уровень объекта исследования
a,b – параметры уравнений фактической и прогнозной линии
t – порядковый номер фактического и прогнозного уравнения.
Для нахождения неизвестных параметров a и b применяется метод наименьших квадратов.
Параметры уравнения a и b определяется по формулам, они применимы при условии, что средний уровень динамического ряда условно применять за начальный уровень.
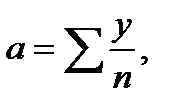
где y – фактическое значение
n – порядковый номер уравнений.

где t – отклонение порядкового номера от среднего номера.
Для расчета суммы фактической объекта исследования динамического ряда, а также отклонений фактической от выровненной в динамическом ряду составляем таблицу.
Исходные данные фактической за ряд лет приведены в приложении. Значение суммы фактической объекта определяем путем суммирования с 2008 по 2012 гг.
Порядковый номер уровней определяем началом тренда, то есть динамического ряда. В моем примере 2008 г. принят за 1 порядковый номер. Срединный номер или центральное положение порядкового уровня определяется исходя из количества порядковых номеров в ряду. В моем примере их 5, поэтому центральное положение порядкового уровня выпадает на 2010 г.
Отклонение порядкового номера от среднего номера определяется путем распределения его от центрального положения вверх с отрицательным порядковым номером, а в низ с положительным порядковым номером.
Квадратное отклонение определяется путем возведения отклонения порядкового уровня в квадрат.
Произведение значений фактической урожайности на отклонение порядкового номера, знаки учитываем.
|
|
|
Коэффициент а характеризует значение сглаженной (выровненной) объекта исследования по прямой линии для центрального в динамическом ряду года, принято за начало отсчета.
Коэффициент в характеризует среднее значение уменьшения объекта исследования в год.
Определяем выровненные уровни объекта исследования по рассчитанному уравнению за период с 2008 по 2014 гг.
Оцениваем степень приближения выровненной объекта исследования к фактической следующим образом:
а) определяем отклонение фактической объекта исследования от выровненной по формуле:

б) определяем квадратное отклонение фактической объекта исследования от выровненной:
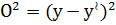
в) определение суммы квадратных отклонений фактической объекта исследования от выровненной.
2. По уравнению параболы.
Выравнивание и прогнозирование объекта исследования имеет вид:

где уi' – выровненный и прогнозный уровень объекта исследования
a,b,с – параметры уравнений фактической и прогнозной линии
t – порядковый номер фактического и прогнозного уравнения.
Для нахождения неизвестных параметров abс применяется формулы:
 ;
;
 ;
;

Эти формулы применяются при условии, что средний уровень динамического ряда условно принят за начальный уровень. Для определения параметров а, в и с необходимо рассчитать значение сумм фактической урожайности зерновых, порядковый номер уровней, квадрат отклонения, отклонение в 4 степени порядковых номеров, произведение значений фактической урожайности зерновых и отклонения порядкового номера, произведение значений фактической урожайности на квадрат отклонения.
Коэффициент а характеризует значение сглаженной объекта исследования (выровненной) для центрального в динамическом ряду года.
Коэффициент в характеризует среднее значение уменьшения (если со знаком минус) или увеличения (если знак плюс) объекта исследования.
|
|
|
Коэффициент с характеризует степень уменьшения прироста объекта исследования (если знак минус), степень нарастания прироста за год (если знак плюс).
Определяем выровненные уровни объекта исследования по рассчитанному уравнению за период с 2008 по 2012 гг. Далее определяем прогнозные уровни объекта исследования за период с 2013 по 2014 гг.
Оцениваем степень приближения выровненной объекта исследования к фактической следующим образом:
а) определяем отклонение фактической объекта исследования от выровненной по формуле:

б) определяем квадратное отклонение фактической объекта исследования от выровненной:
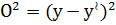
в) определение суммы квадратных отклонений фактической объекта исследования от выровненной.
| уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическая площадь жилищного фонда, тыс. м^2. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненная площадь жилищного фонда, тыс. м^2. | отклонение фактической площади жилищного фонда от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненная площадь жилищного фонда, тыс. м^2. | отклонение фактической площади жилищного фонда от выровненной | квадрат отклонения |
| у | n | T | t² | yt | y´ | o | o² | T | yt² | y´ | o | o² | |
| 69,00 | -2 | -138,00 | 69,40 | -0,40 | 0,16 | 276,00 | 68,69 | 0,31 | 0,10 | ||||
| 69,00 | -1 | -69,00 | 69,10 | -0,10 | 0,01 | 69,00 | 69,46 | -0,46 | 0,21 | ||||
| 69,00 | 0,00 | 68,80 | 0,20 | 0,04 | 0,00 | 69,51 | -0,51 | 0,26 | |||||
| 70,00 | 70,00 | 68,50 | 1,50 | 2,25 | 70,00 | 68,86 | 1,14 | 1,31 | |||||
| 67,00 | 134,00 | 68,20 | -1,20 | 1,44 | 268,00 | 67,49 | -0,49 | 0,24 | |||||
| 67,90 | 65,40 | ||||||||||||
| 67,60 | 62,60 | ||||||||||||
| 344,00 | -3,00 | 344,00 | 3,90 | 683,00 | 344,00 | 2,11 |
Таблица 1 - Прогнозирование площади жилищного фонда в муниципальном образовании пгт. Палана
Вывод: таким образом, сумма квадратов отклонений фактической площади ЖФ от выровненной полученной по уравнению параболы меньше, чем по уравнению прямой линии от сюда следует, прогнозирование площади ЖФ на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере площадь ЖФ на 2014 г. прогнозируется равной 62,6 тыс. м2.
|
|
|
По уравнению прямой: а=68,8; в=-0,3. По уравнению параболы: а=69,5; в=-0,3; с=-0,35.

| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| Годы | фактическая численность, чел. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненная численность, чел | отклонение фактической численности от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненная численность | отклонение фактической численности от выровненной | квадрат отклонения |
| у | N | t | t² | yt | y´ | o | o² | t^4 | yt² | y´ | o | o² | |
| 3620,00 | -2 | 7240,00 | 3612,60 | 7,40 | 54,76 | 14480,00 | 3676,60 | -56,60 | 3203,56 | ||||
| 3591,00 | -1 | 3591,00 | 3472,20 | 118,80 | 14113,44 | 3591,00 | 3440,20 | 150,80 | 22740,64 | ||||
| 3155,00 | 0,00 | 3331,80 | -176,80 | 31258,24 | 0,00 | 3267,80 | -112,80 | 12723,84 | |||||
| 3159,00 | 3159,00 | 3191,40 | -32,40 | 1049,76 | 3159,00 | 3159,40 | -0,40 | 0,16 | |||||
| 3134,00 | 6268,00 | 3051,00 | 83,00 | 6889,00 | 12536,00 | 3115,00 | 19,00 | 361,00 | |||||
| 2910,60 | 3134,60 | ||||||||||||
| 2770,20 | 2917,02 | ||||||||||||
| 16659,00 | -1404,00 | 16659,00 | 53365,20 | 33766,00 | 16659,00 | 39029,20 |
Таблица 2 - Прогнозирование численности населения муниципального образования пгт. Палана
Вывод: таким образом, сумма квадратов отклонений фактической численности от выровненной полученной по уравнению параболы значительно меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование численности на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере численность на 2014 г. прогнозируется равной 2917 чел.
|
|
|
По уравнению прямой: а=3331,8; в=140,4. По уравнению параболы: а=3267,8; в=140,4; с=32.

Таблица 3 –Прогнозирование численности родившихся за год в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое число родившихся, чел. | порядковый номер ноуравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное число родившихся, чел | отклонение фактического числа родившихся от выровненной | квадрат отклонения | отклонение в четвертой степени п порядкового номера | произведение значений | выровненное число родившихся | отклонение фактического числа родившихся от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 38,00 | -2 | -76,00 | 36,80 | 1,20 | 1,44 | 152,00 | 37,80 | 0,20 | 0,04 | ||||
| 43,00 | -1 | -43,00 | 41,90 | 1,10 | 1,21 | 43,00 | 41,40 | 1,60 | 2,56 | ||||
| 40,00 | 0,00 | 47,00 | -7,00 | 49,00 | 0,00 | 46,00 | -6,00 | 36,00 | |||||
| 58,00 | 58,00 | 52,10 | 5,90 | 34,81 | 58,00 | 51,60 | 6,40 | 40,96 | |||||
| 56,00 | 112,00 | 57,20 | -1,20 | 1,44 | 224,00 | 58,20 | -2,20 | 4,84 | |||||
| 62,30 | 65,80 | ||||||||||||
| 67,40 | 74,40 | ||||||||||||
| 235,00 | 51,00 | 235,00 | 87,90 | 477,00 | 235,00 | 84,40 |
Вывод: таким образом, сумма квадратов отклонений фактической рождаемости от выровненной полученной по уравнению параболы значительно меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование рождаемости на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере число родившихся на 2014 г. прогнозируется равной 74 чел.
По уравнению прямой: а=47; в=5,1. По уравнению параболы: а=46; в=5,1; с=0,5.

Таблица 4 –Прогнозирование среднемесячной заработной платы в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое число среднемесячной заработанной платы, тыс. руб. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное число среднемесячной заработанной платы, тыс. руб. | отклонение фактического числа заработанной платы от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненное число заработанной платы, тыс. руб. | отклонение фактического числа заработанной платы от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 34,70 | -2 | -69,40 | 35,08 | -0,38 | 0,14 | 138,80 | 34,75 | -0,05 | 0,00 | ||||
| 38,40 | -1 | -38,40 | 38,35 | 0,05 | 0,00 | 38,40 | 38,51 | -0,11 | 0,01 | ||||
| 42,60 | 0,00 | 41,62 | 0,98 | 0,96 | 0,00 | 41,95 | 0,65 | 0,42 | |||||
| 44,30 | 44,30 | 44,89 | -0,59 | 0,35 | 44,30 | 45,05 | -0,75 | 0,57 | |||||
| 48,10 | 96,20 | 48,16 | -0,06 | 0,00 | 192,40 | 47,83 | 0,27 | 0,07 | |||||
| 51,43 | 50,28 | ||||||||||||
| 54,70 | 52,40 | ||||||||||||
| 208,10 | 32,70 | 208,10 | 1,46 | 413,90 | 208,10 | 1,08 |
Вывод: таким образом, сумма квадратов отклонений фактической заработанной платы от выровненной полученной по уравнению параболы меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование заработанной платы на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере ЗП на 2014 г. прогнозируется равной 52,4 тыс. руб.
|
|
|
По уравнению прямой: а=41,6; в=3,27. По уравнению параболы: а=41,9; в=3,27; с=0,16.

Таблица 5 –Прогнозирование налогового дохода в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое число налогового дохода, тыс. руб. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное число налогового дохода, тыс. руб. | отклонение фактического числа налогового дохода от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненное число налогового дохода, тыс. руб. | отклонение фактического числа налогового дохода от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 49291,00 | -2 | -98582,00 | 45683,00 | 3608,00 | 13017664,00 | 197164,00 | 48826,57 | 464,43 | 215693,90 | ||||
| 43679,00 | -1 | -43679,00 | 46181,10 | -2502,10 | 6260504,41 | 43679,00 | 44609,31 | -930,31 | 865484,67 | ||||
| 43540,00 | 0,00 | 46679,20 | -3139,20 | 9854576,64 | 0,00 | 43535,63 | 4,37 | 19,11 | |||||
| 46530,00 | 46530,00 | 47177,30 | -647,30 | 418997,29 | 46530,00 | 45605,51 | 924,49 | 854673,84 | |||||
| 50356,00 | 100712,00 | 47675,40 | 2680,60 | 7185616,36 | 201424,00 | 50818,97 | -462,97 | 214342,54 | |||||
| 48173,50 | 59176,00 | ||||||||||||
| 48671,60 | 70676,60 | ||||||||||||
| 233396,00 | 4981,00 | 233396,00 | 36737358,70 | 488797,00 | 233396,00 | 2150214,06 |
Вывод: таким образом, сумма квадратов отклонений фактической дохода от налогов от выровненной полученной по уравнению параболы значительно меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование дохода от налогов на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере дохода от налогов на 2014 г. прогнозируется равной 70676 тыс.руб.
По уравнению прямой: а=46679,2; в=498,1. По уравнению параболы: а=43535,6; в=498,1; с=151,7.

Таблица 6 –Прогнозирование ЛПХ в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое число ЛПХ, ед. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное число ЛПХ, ед. | отклонение фактического числа ЛПХ от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненное число ЛПХ, ед. | отклонение фактического числа ЛПХ от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 21,00 | -2 | -42,00 | 23,20 | -2,20 | 4,84 | 84,00 | 21,20 | -0,20 | 0,04 | ||||
| 21,00 | -1 | -21,00 | 20,20 | 0,80 | 0,64 | 21,00 | 21,20 | -0,20 | 0,04 | ||||
| 21,00 | 0,00 | 17,20 | 3,80 | 14,44 | 0,00 | 19,20 | 1,80 | 3,24 | |||||
| 13,00 | 13,00 | 14,20 | -1,20 | 1,44 | 13,00 | 15,20 | -2,20 | 4,84 | |||||
| 10,00 | 20,00 | 11,20 | -1,20 | 1,44 | 40,00 | 9,20 | 0,80 | 0,64 | |||||
| 8,20 | 1,20 | ||||||||||||
| 5,20 | -8,80 | ||||||||||||
| 86,00 | -30,00 | 86,00 | 22,80 | 158,00 | 86,00 | 8,80 |
Вывод: таким образом, сумма квадратов отклонений фактической количества ЛПХ от выровненной полученной по уравнению параболы значительно меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование количества ЛПХ на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере количества ЛПХ на 2014 г. прогнозируется равной -8 ед.
По уравнению прямой: а=17,2; в=-3. По уравнению параболы: а=19,2; в=-3; с=-1.

Таблица 7 – Прогнозирование поголовья скота ЛПХ в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое поголовье скота в ЛПХ, ед. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное поголовье скота в ЛПХ, ед. | отклонение фактического поголовья скота в ЛПХ от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненное поголовье скота в ЛПХ, ед. | отклонение фактического поголовья скота в ЛПХ от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 51,00 | -2 | -102,00 | 52,20 | -1,20 | 1,44 | 204,00 | 49,49 | 1,51 | 2,29 | ||||
| 50,00 | -1 | -50,00 | 51,70 | -1,70 | 2,89 | 50,00 | 53,06 | -3,06 | 9,35 | ||||
| 54,00 | 0,00 | 51,20 | 2,80 | 7,84 | 0,00 | 53,91 | 0,09 | 0,01 | |||||
| 55,00 | 55,00 | 50,70 | 4,30 | 18,49 | 55,00 | 52,06 | 2,94 | 8,66 | |||||
| 46,00 | 92,00 | 50,20 | -4,20 | 17,64 | 184,00 | 47,49 | -1,49 | 2,21 | |||||
| 49,70 | 40,20 | ||||||||||||
| 49,20 | 30,20 | ||||||||||||
| 256,00 | -5,00 | 256,00 | 48,30 | 493,00 | 256,00 | 22,51 |
Вывод: таким образом, сумма квадратов отклонений фактической поголовья скота от выровненной полученной по уравнению параболы значительно меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование поголовья скота на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере поголовья скота на 2014 г. прогнозируется равной 30,2 ед.
По уравнению прямой: а=51,2; в=-0,5. По уравнению параболы: а=53,9; в=-0,5; с=-1,35.

Таблица 8 – Прогнозирование протяженности автомобильных дорог в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическая протяженность автомобильных дорог, км. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненная протяженность автомобильных дорог, км. | отклонение фактической протяженности автомобильных дорог от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненная протяженность автомобильных дорог, км. | отклонение фактической протяженности автомобильных дорог от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 21,00 | -2 | -42,00 | 21,00 | 0,00 | 0,00 | 84,00 | 21,00 | 0,00 | 0,00 | ||||
| 21,00 | -1 | -21,00 | 21,00 | 0,00 | 0,00 | 21,00 | 21,00 | 0,00 | 0,00 | ||||
| 21,00 | 0,00 | 21,00 | 0,00 | 0,00 | 0,00 | 21,00 | 0,00 | 0,00 | |||||
| 21,00 | 21,00 | 21,00 | 0,00 | 0,00 | 21,00 | 21,00 | 0,00 | 0,00 | |||||
| 21,00 | 42,00 | 21,00 | 0,00 | 0,00 | 84,00 | 21,00 | 0,00 | 0,00 | |||||
| 21,00 | 0,00 | 21,00 | |||||||||||
| 21,00 | 21,00 | ||||||||||||
| 105,00 | 0,00 | 105,00 | 0,00 | 210,00 | 105,00 | 0,00 |
Вывод: таким образом, сумма квадратов отклонений фактической протяженности дорожного полотна от выровненной полученной по уравнению параболы неизменно к уравнению прямой линии, от сюда следует, что прогнозирование протяженности дорожного полотна на среднесрочную перспективу осуществляться не будет.
По уравнению прямой: а=21; в=0. По уравнению параболы: а=21; в=0; с=0.
Таблица 9 – Прогнозирование земель населенного пункта в муниципальном образовании пгт. Плана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическая площадь земель нп, ед. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненная площадь земель нп, ед. | отклонение фактической площади земель нп, от выровненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненная площадь земель нп, ед. | отклонение фактической площади земель нп от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t | yt² | y´ | o | o² | |
| 46,00 | -2 | -92,00 | 47,00 | -1,00 | 1,00 | 184,00 | 47,29 | -1,29 | 1,65 | ||||
| 55,00 | -1 | -55,00 | 52,00 | 3,00 | 9,00 | 55,00 | 51,86 | 3,14 | 9,88 | ||||
| 55,00 | 0,00 | 57,00 | -2,00 | 4,00 | 0,00 | 56,71 | -1,71 | 2,94 | |||||
| 61,00 | 61,00 | 62,00 | -1,00 | 1,00 | 61,00 | 61,86 | -0,86 | 0,73 | |||||
| 68,00 | 136,00 | 67,00 | 1,00 | 1,00 | 272,00 | 67,29 | 0,71 | 0,51 | |||||
| 72,00 | 73,00 | ||||||||||||
| 77,00 | 77,66 | ||||||||||||
| 285,00 | 50,00 | 285,00 | 16,00 | 572,00 | 285,00 | 15,71 |
Вывод: таким образом, сумма квадратов отклонений фактической площади НП от выровненной полученной по уравнению параболы меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование площади НП на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере площадь НП на 2014 г. прогнозируется равной 77,6 ед.
По уравнению прямой: а=57; в=5. По уравнению параболы: а=56,7; в=5; с=0,14.

Таблица 10 – Прогнозирование производство электроэнергии в муниципальном образовании пгт. Палана
| Уравнение прямой линии | по уравнению параболы | ||||||||||||
| годы | фактическое производство электроэнергии, млн. руб. | порядковый номер уравнений | отклонение порядкового номера от среднего номера | квадрат отклонения | произведение значений | выровненное производство электроэнергии, млн. руб. | отклонение фактического производства электроэнергии от выравненной | квадрат отклонения | отклонение в четвертой степени порядкового номера | произведение значений | выровненное производство электроэнергии, млн. руб. | отклонение фактического производства электроэнергии от выровненной | квадрат отклонения |
| у | n | t | t² | yt | y´ | o | o² | t^4 | yt² | y´ | o | o² | |
| 218,60 | -2 | -437,20 | 243,90 | -25,30 | 640,09 | 874,40 | 233,46 | -14,86 | 220,73 | ||||
| 275,50 | -1 | -275,50 | 248,89 | 26,61 | 708,09 | 275,50 | 254,11 | 21,39 | 457,47 | ||||
| 289,30 | 0,00 | 253,88 | 35,42 | 1254,58 | 0,00 | 264,32 | 24,98 | 623,86 | |||||
| 209,40 | 209,40 | 258,87 | -49,47 | 2447,28 | 209,40 | 264,09 | -54,69 | 2991,15 | |||||
| 276,60 | 553,20 | 263,86 | 12,74 | 162,31 | 1106,40 | 253,42 | 23,18 | 537,44 | |||||
| 268,85 | 232,30 | ||||||||||||
| 273,84 | 200,74 | ||||||||||||
| 1269,40 | 49,90 | 1269,40 | 5212,35 | 2465,70 | 1269,40 | 4830,66 |
Вывод: таким образом, сумма квадратов отклонений фактической производительности электроэнергии от выровненной полученной по уравнению параболы меньше, чем по уравнению прямой линии, от сюда следует, что прогнозирование производительности электроэнергии на среднесрочную перспективу будем осуществлять по уравнению параболы, распространяя изменения функции из области наблюдения на область, лежащую вне отрезка наблюдения. В нашем примере производительность электроэнергии на 2014 г. прогнозируется равной 200,74 млн.руб.
По уравнению прямой: а=253,8; в=4,99. По уравнению параболы: а=246,3; в=4,99; с=-5,22.

Заключение
Прогнозирование заключается в исследовании имеющихся наблюдений математическими методами, формировании зависимости, связывающие характеристики объекта со временем или характеристиками других объектов, и вычислении с помощью найденной зависимости характеристик объекта на интервал упреждения.
Процесс прогнозирования должен быть организован в виде некоторой системы, которая обеспечивает ввод и преоб
|
|
|


