 |
«Определение прямоугольных координат по топографической карте»
|
|
|
|
Вопрос №35.
«Определение прямоугольных координат по топографической карте»
(практический вопрос)
Прямоугольные координаты определяют с помощью координатной (километровой) сетки, представляющей собой сеть линий, параллельных экватору и осевому меридиану зоны.
1. Для определения прямоугольных координат заданной точки (рис. 4) сначала нужно найти координаты левого нижнего угла квадрата, образованного линиями километровой сетки, в котором расположена точка. Т. е. X0 и Y0, записанные в метрах.
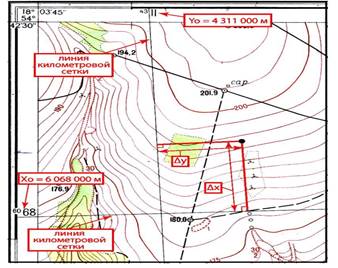
Рис. 4. Определение прямоугольных координат.
2. Далее необходимо из заданной точки опустить перпендикуляры к левой и нижней линиям километровой сетки, измерить с помощью циркуля-измерителя длины отрезков и перевести, используя численный масштаб, в метры на местности. Получим приращения прямоугольных координат ∆ x и ∆ y.
3. Искомые абсцисса и ординаты рассчитываются по формулам:
X = X0 + ∆ xY = Y0 + ∆ y.
Ссылка на короткое и доходчивое видео по выполнению:
НАХОЖДЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ НА ТОПОГРАФИЧЕСКОЙ КАРТЕ. ТОПОГРАФИЯ - YouTube
Вопрос №36.
«Классификации проекций по способу построения»
По способу построения выделяют следующие группы проекций:
1. Цилиндрические – проекции, которые получаются путем переноса градусной сетки с глобуса на боковую поверхность цилиндра касательного или секущего к этому глобусу. На секущем цилиндре проекции строят для уменьшения величины искажения на периферии карты.
2. Конические – это проекции, которые получаются путем переноса градусной сетки с глобуса на боковую поверхность конуса, касательного или секущего к данному глобусу.
|
|
|
3. Азимутальные проекции получаются путем переноса градусной сетки с глобуса на плоскость, касательную к этому глобусу в одной точке.
4. Условные проекции строятся без использования вспомогательных поверхностей на основе математических расчетов.
Вопрос №37.
«Цилиндрические проекции»
Цилиндрические проекции, которые получаются путем переноса градусной сетки с глобуса на боковую поверхность цилиндра касательного или секущего к этому глобусу. На секущем цилиндре проекции строят для уменьшения величины искажения на периферии карты.
1. Нормальные - когда ось цилиндра и ось глобуса совпадают. В нормальных цилиндрических проекциях параллели и меридианы – прямые взаимно перпендикулярные линии, образующие квадраты или прямоугольники.
2. Поперечные проекции – когда ось цилиндра и ось глобуса находятся под прямым углом друг к другу. В поперечной цилиндрической равновеликой проекции Гаусса-Крюгера строятся топографические карты.
3. Косые цилиндрические проекции получаются, когда ось цилиндра и ось глобуса составляют острый угол. В косой цилиндрической проекции Соловьева строится карта России для младших школьников. Форма градусной сетки в этой проекции создает впечатление сферичности поверхности Земли, на ней изображается весь сектор Арктики вплоть до точки Северного полюса.
Вопрос №38.
«Определение географических координат по топографической карте»
(практический вопрос)
1. Географическая широта φ точки - это угол между направлением отвесной линии, проходящей через заданную точку, и плоскостью экватора.
2. Географическая долгота λ точки - это двугранный угол между плоскостью меридиана, проходящего через заданную точку и плоскостью начального (Гринвичского) меридиана.
Для определения географических координат точки на карте построена минутная рамка (рис. 9). Ее стороны разделены на чередующиеся белые и черные отрезки, каждая равна одной минуте. Каждый минутный отрезок размечен точками по 10 секунд каждая.
|
|
|

Рис. 9. Определение географических координат
1. Чтобы определить широту и долготу заданной точки, необходимо опустить перпендикуляры соответственно на западный меридиан и южную параллель карты (рис. 9).
2. Затем к начальным значениям широты и долготы юго-западного угла рамки, подписанным на карте, прибавить число минут и секунд, подсчитанных от начальных значений φ и λ до опущенных 22 перпендикуляров.
Пример: По учебной карте У - 34 - 37 - В - в (рис. 9) определить географические координаты пункта триангуляции 197, 1 (квадрат (65-08)).
ü Опустим перпендикуляры на западный меридиан (т. е. проведем параллель через заданную точку) и южную параллель (т. е. проведем меридиан через заданную точку). Широта юго-западного угла рамки равна 54°40', долгота - 18°00'. Число полных минут (чередующихся черных и белых полос) до опущенного перпендикуляра на меридиан составляет 0, а секунд (число точек) - 4 и на глаз определяем десятые (2). Отметим, что 1' = 60" (секунд), т. е. одна секундная точка на карте равна 10".
ü Тогда искомая широта равна φ = 54°40' + 0' + 4, 2 ∙ 10" = 54° 40' 42"
ü До опущенного на параллель перпендикуляра подсчитываем число полных минут (черная и белая полосы) - 2, секунд – 0 точек и оцениваем на глаз десятые (3), вычисляем долготу:
λ = 18°00' + 2' + 0, 3 ∙ 10" = 18°02' 03".
|
|
|


